All published articles of this journal are available on ScienceDirect.
Liquid-liquid Equilibrium in Systems Containing Olive Oil, Free Fatty Acids, Ethanol and Water
Abstract
This paper reports experimental data and the thermodynamic modeling of the liquid-liquid equilibrium systems with triacylglycerols, free fatty acids (obtained from olive oil), ethanol and water. The experimental data were fitted using the UNIQUAC model, in which absolute deviation of 1.28 % and root mean square deviation of 2.10 % between experimental and calculated mass fraction of the components in each phase were obtained. The results from this study can be complementary to investigations of more complex liquid-liquid equilibrium of systems containing diacylglycerols and monoacylglcerols of olive oil in hydroalcoholic solutions, once such systems will mostly also contain triacylglycerols and free fatty acids on its composition. Diacylglycerols are obtained from different reaction processes and can be purified by liquid-liquid extraction at mild conditions of temperature and pressure, what justifies the experimental and theoretical approach made in this work.
NOMENCLATURE
DAG - diacylglycerol
FFA - free fatty acid
MAG - monoacylglycerol
nc - number of compounds in the system
nf - total number of phases
NP - total number of tie-lines
TAG - triacylglycerol
xijkcalc - calculated mass fraction of component i in phase j for the k tie-line
xijkexp - experimental mass fraction of component i in phase j for the k tie-line
σj2 - variance of the experimental phase j
1. INTRODUCTION
Diets that are rich in fats and oils represent a risk factor for obesity and heart diseases so that physicians and other professionals related to health care area have recommended a reduction in such dietary habits. Since fats and oils are sources of essential fatty acids and liposoluble vitamins, the ingestion of this kind of food is recommended in a diary balanced diet [1]. However, low fat diets are usually not tolerated for long periods, due to the fact that the presence of fat increases the palatability of the food. An alternative to the reduction of the amount of fat consumed is the replacement of the conventional edible oil, which is rich in triacylglycerols molecules, by a diacylglycerol rich oil. Such enriched types of oil have been well accepted by consumers of fatty foods and studies have indicated that its consumption in replacement by the conventional oil can prevent health problems that are related to rich triacylglycerol oils consumption [2, 3].
Diacylglycerols can be produced by glycerol esterification processes, glycerolysis of triacylglycerols or from the partial hydrolysis of triacylglycerols [4]. Independently of the process used, the final product will contain a mixture of triacylglycerols, diacylglycerols, monoacylglycerols and free fatty acids (FFA), which are molecules with main polar groups, and so can be easily separated from glycerol and water present in the reactant medium. A further separation process is normally necessary to separate the diacylglycerols from the other molecules, and that can be achieved with distillation [5] or liquid-liquid extraction with polar solvents [6].
Distillation of oil molecules is a process related to high temperatures and high vacuum conditions (since are molecules with very high molecular weight and low volatility), different from liquid-liquid extraction that can be performed at ambient conditions. In fact, the temperature required for a liquid-liquid extraction process involving oil molecules should just be high enough to avoid the formation of a solid phase in the system.
For an appropriate process and equipment design, mathematical models are usually required. Voll et al. [6] obtained liquid-liquid UNIQUAC and NRTL interaction parameters for the system TAG + DAG + MAG + FFA + ethanol + water by correlating experimental data with the Gibbs free energy models, and verified the potential of DAG enrichment by liquid-liquid extraction strategy using ethanol and water as solvents. The water phase tends to have less TAG molecules, due to its higher hydrophobicity when compared to DAG, MAG and FFA. Since DAG presents higher hydrophobicity than MAG and FFA, simulations indicate that multiple equilibrium stages will ensure DAG enrichment in the oil.
Since a liquid-liquid system with 6 components demands 30 binary interaction parameters for Gibbs free energy models it is desirable that some of these parameters are previously known from smaller systems that contain the same components. In this context, the main subject of this work was to determine the binary interaction parameters between TAG, FFA (both from olive oil), ethanol and water from ternary systems comprising these 4 components. This procedure can reduce from 30 to 18 the number of unknown parameters to be determined in a 6 component liquid-liquid system.
Gonçalves and Meirreles [7] and Chiyoda et al. [8] presented experimental data and thermodynamic modeling of liquid-liquid equilibrium of palm oil + fatty acids (palmitic and/or oleic acid) + ethanol + water and soybean oil + linoleic acid + ethanol + water systems, respectively. The first study has shown that the behavior of the main free fatty acids of palm oil (palmitic and oleic) are quite similar in liquid-liquid equilibrium. However, for a high water content in the system (12.41 wt%), the thermodynamic model UNIQUAC overestimated or underestimated the different free fatty acids distribution coefficients depending on the acidity level. In the present work, it was an intention to use free fatty acids obtained from the own edible oil (by hydrolysis) used in the experiments. Olive oil is one of the edible oils with higher concentration in one particular fatty acid (in this case, the oleic acid)[9], and such fact probably improves the chances that the TAG and free fatty acids from this oil behave as pseudo-components for the modeling purposes. For that reason, olive oil was chosen as substrate in the present work.
2. MATERIALS AND METHODS
2.1. Materials
The edible oil used in this work was extra virgin olive oil from Andorinha brand (purchased in Curitiba, Brazil) with 0.8% of maximum acidity. Commercial enzyme Lipozyme RM IM was purchased from Sigma-Aldrich. n-Hexane (Panreac) was used for enzyme filtration. Bi distillate water, NaOH, Phenolphthalein (both from Vetec) and absolute ethanol with a purity of 99.8% (Sigma-Aldrich) were used in acidity determinations and liquid-liquid experiments. All chemicals were used without further treatment.
2.2. Methods
2.2.1. Olive Oil Hydrolysis
A hydrolysis reaction of olive oil was performed to obtain a product with high free fatty acids content. Precise amounts of oil (184.3702 g) and water (80% relative to the mass of oil), weighed in a Shimadzu analytical balance, were added in a 500 mL glass reactor, which was stirred at 300 rpm with an IKA magnetic stirrer and maintained at 50 ºC. After one hour of stirring, the enzyme (1% relative to the total mass of oil and water) was added to the system. The acidity in the reactant medium was monitored using a titration method until no change were been observed. At the end of the reaction, a product with 97 wt% of free fatty acids was obtained.
2.2.2. Free Fatty Acid Quantification
Free fatty acid quantification was performed according to the procedure described by Voll et al. [6]. The molar mass of FFA obtained from olive oil was considered 277.875 g.mol-1. This value was estimated as a weighted mean of molar mass of different free fatty acids present in the olive oil used in this work (15.8 wt% of saturated, 77.5 wt% of unsaturated and 6.7 wt% of polyunsaturated free fatty acids). Palmitic acid (256.429 g.mol-1) was used to represent the saturated acids, while oleic acid (282.467 g.mol-1) and linoleic acid (280.451 g.mol-1) were used to represent the unsaturated and polyunsaturated acids, respectively.
2.2.3. Water Quantification
The water content present in each of samples of liquid phases in equilibrium was determined by Karl Fischer titration.
2.2.4. LLE Measurements
Liquid-liquid equilibrium experiments were carried out in a jacket-glass cell (40 mL), which was maintained at constant temperature (328.2 K or 298.2 K) by a thermostatic bath. Then, the previously determined amounts of olive oil, free fatty acids of olive oil, ethanol and water were added to the cell (a final volume of around 30 ml was usually obtained). The system was magnetically stirred to promote the intimate contact between the liquid phases. After 4 hours, the stirrer was turn down to allow the complete phases separation. Samples (about 5 mL) of each phase were collected 24 hours after the suspension of agitation.
As mentioned before the water was quantified by Karl Fisher titration, while free fatty acids were quantified by acid-base titration. The amounts of olive oil and ethanol were then determined by mass balance after the evaporation of the ethanol and water of the sample, which was performed in an oven at 120 ºC until constant weight (previous experiments were made to verify that in such condition no oil/free fatty acid is volatilized).
2.2.5. LLE Modeling
The liquid–liquid equilibrium calculations were performed by applying the multiphase liquid-liquid split calculation algorithm with a phase stability test [10]. In a previous work [6], it was shown that UNIFAC model is unsatisfactory when compared to experimental liquid-liquid equilibrium data containing water, ethanol, free fatty acids and acylglycerols, while NRTL model presented a similar but slightly inferior correlation capability when compared to the UNIQUAC model. For that reason, only the latter was used for the activities coefficient calculations in this study. A weighed least square objective function was used to optimize the binary interaction parameter for the thermodynamic model, as presented in equation (1).
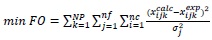 |
(1) |
Where, xijkcalc and xijkexp are the calculated and experimental mass fractions, respectively, of component i in the phase j related to tie line k, NP is the total number of tie lines, nf is the total number of phases, nc is the number of components in the system and σj2 is the variance of component i in the experimental phase j.
The standard error for composition in each phase was estimated as 0.0005 (in mass fraction basis). For the minimization of the objective function (Equation 1), the Particle Swarm Optimization algorithm (PSO) was used [10] for an initial guess, while the modified Simplex method [11] was used for final value of binary parameters optimization. Twelve experimental tie lines, which include 70 experimental mass fractions information for TAG, FFA, ethanol and water, were used in the parameters estimation procedure.
To evaluate the quality of the UNIQUAC correlation to the experimental data, the root mean square deviation (rmsd%) and the absolute deviation (AD%) were calculated as presented in equations (2) and (3), respectively:
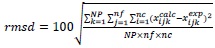 |
(2) |
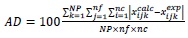 |
(3) |
3. RESULTS AND DISCUSSION
The tie lines measured at 328.2 K for the three ternary systems, which were used in the estimation of UNIQUAC parameters, are presented in Table 1. Tables 2 and 3 present the ternary system obtained at 298.2 K and the quaternary system at 328.2 K, respectively. The experimental data presented in Table 2 were not used for the parameters estimation of the excess Gibbs free energy model used in this work. These data were used to check the prediction capability of the thermodynamic model used.
Experimental liquid-liquid equilibrium data in mass fraction (wt%) for TAG(1) + free fatty acid (FFA)(2) + ethanol(3) + water(4) at 328.2 K.
| Overall Composition | Oil-rich Phase | Alcohol-rich Phase | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| wt1(%) | wt2(%) | wt3(%) | wt4(%) | wt1(%) | wt2(%) | wt3(%) | wt4(%) | wt1(%) | wt2(%) | wt3(%) | wt4(%) |
| 0 | 34.30 | 18.87 | 46.83 | 0 | 90.96 | 7.12 | 1.92 | 0 | 0.17 | 23.66 | 76.17 |
| 0 | 33.71 | 35.77 | 30.52 | 0 | 63.29 | 28.30 | 8.41 | 0 | 0.30 | 46.59 | 53.11 |
| 0 | 30.35 | 40.69 | 28.96 | 0 | 51.42 | 34.38 | 14.20 | 0 | 1.39 | 50.88 | 47.73 |
| 0 | 40.07 | 12.84 | 47.09 | 0 | 94.46 | 4.21 | 1.33 | 0 | 0.41 | 21.55 | 78.04 |
| 43.43 | 0 | 45.86 | 10.71 | 93.06 | 0 | 6.45 | 0.49 | 0.39 | 0 | 80.36 | 19.25 |
| 39.34 | 0 | 40.66 | 20.00 | 94.12 | 0 | 5.33 | 0.55 | 0.23 | 0 | 67.84 | 31.93 |
| 29.32 | 0 | 40.69 | 29.99 | 95.65 | 0 | 3.76 | 0.59 | 0.45 | 0 | 56.44 | 43.11 |
| 48.35 | 0 | 51.65 | 0 | 74.59 | 0 | 25.41 | 0 | 11.99 | 0 | 88.01 | 0 |
| 31.55 | 4.92 | 63.53 | 0 | 42.27 | 4.29 | 53.44 | 0 | 22.4 | 5.33 | 72.27 | 0 |
Experimental liquid-liquid equilibrium data in mass fraction (wt%) for TAG(1) + ethanol(3) + water(4) at 298.2 K.
| Overall Composition | Oil-rich Phase | Alcohol-rich Phase | ||||||
|---|---|---|---|---|---|---|---|---|
| wt1(%) | wt3(%) | wt4(%) | wt1(%) | wt3(%) | wt4(%) | wt1(%) | wt3(%) | wt4(%) |
| 41.13 | 46.93 | 11.94 | 96.44 | 3.38 | 0.18 | 0.31 | 77.68 | 22.01 |
| 33.59 | 33.38 | 33.03 | 97.01 | 2.36 | 0.63 | 0.71 | 49.63 | 49.66 |
| 24.19 | 31.76 | 44.05 | 98.04 | 1.75 | 0.21 | 0.12 | 44.50 | 55.38 |
The ri and qi values used for the UNIQUAC model are presented in Table 4, while the estimated interaction parameters Aij e Aji are presented in Table 5. It must be pointed out that only 10 parameters were adjusted in the present work, since the interaction parameters between ethanol and water were used as obtained by Kanda et al. [12], who studied the LLE of palmitic acid + ethanol + water/glycerol.
Experimental liquid-liquid equilibrium data in mass fraction (wt%) for TAG+FFA(1+2) + ethanol(3) + water(4) at 328.2 K (TAG and FFA composition in the overall compositions of 0.534 and 0.466, respectively).
| Overall Composition | Oil-rich Phase | Alcohol-rich Phase | ||||||
|---|---|---|---|---|---|---|---|---|
| wt1+2(%) | wt3(%) | wt4(%) | wt1+2(%) | wt3(%) | wt4(%) | wt1+2(%) | wt3(%) | wt4(%) |
| 41.08 | 16.61 | 42.31 | 95.92 | 3.28 | 0.80 | 0.06 | 29.10 | 70.84 |
| 37.94 | 23.21 | 38.85 | 91.14 | 8.86 | 1.52 | 0.07 | 35.97 | 63.96 |
| 33.13 | 33.25 | 33.62 | 85.68 | 11.85 | 2.47 | 0.52 | 47.65 | 51.83 |
Parameters ri and qi of each compound (TAG, FFA, ethanol and water) used in this work.
| Compound | ri | qi |
|---|---|---|
| TAG | 38.5601 | 31.2853 |
| FFA | 12.5541 | 10.3364 |
| Ethanol | 2.5755 | 2.588 |
| Water | 0.92 | 1.4 |
Adjusted parameters Aij and Aji for the UNIQUAC model for the systems TAG(1) + FFA(2) + ethanol(3) + water(4).
| Pair i-j | Aij | Aji |
|---|---|---|
| 1-2 | 606.09 | -234.54 |
| 1-3 | 232.46 | -51.21 |
| 1-4 | 331.25 | 817.71 |
| 2-3 | 523.14 | -239.36 |
| 2-4 | 2417.17 | 12.39 |
| 3-4a | 22.48 | 113.04 |
For the binary interaction parameters fitting a set with 9 experimental tie lines was used, which included 52 experimental mass fraction information of TAG, FFA, ethanol and water. The absolute deviation (AD) between the experimental and calculated data was 1.28 %, while the root mean square deviation (rmsd) was calculated as 2.10 % (considering all data, except that from Table 2). The low deviations values indicate that the UNIQUAC model was capable of correlate well the experimental data for the complex system presented in this work. Such conclusion can also be made by observing the comparison between experimental and calculated data in Fig. (1) (data from first to fourth lines of Table 1), Fig. (2), (data from Table 2, for Fig. (2-A) and data from fifth to eighth lines for Fig. (2-B)), Fig. (3) (data from eighth and ninth lines of Table 1) and Fig. (4) (data from Table 3). It is worth mentioning that the experimental data showed in Fig. (2-A) were not used in the interaction parameters estimation, which is indicating that the model can be used for liquid-liquid separation predictions in temperatures that are different from that used to obtain the model parameters.
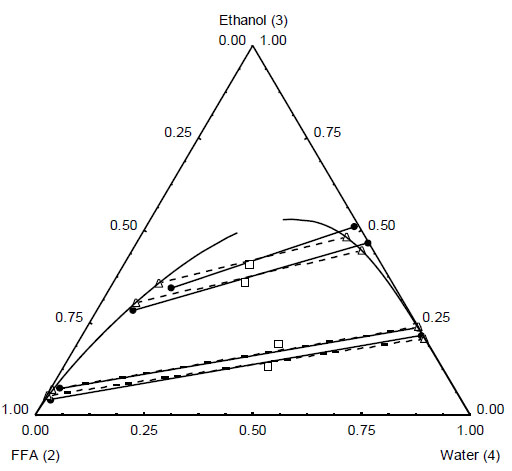
Ternary diagram for the system free fatty acid (FFA)(2) + ethanol(3) + water(4) at T = 328.2 K. Experimental ̶●̶, tie lines, □, overall composition) and UNIQUAC model -Δ-, tie lines; ―, binodal).
One can notice from Figs. (1) and (3) that ethanol and FFA from olive oil are completely miscible. On the other hand, olive oil TAG is only partially miscible in ethanol, as observed in Figs. (2) and (3). A small immiscibility region was observed for the ternary system TAG + FFA + ethanol (Fig. 3). This is expected because ethanol and TAG are partially miscible and, in addition, FFA has good miscibility with both ethanol and TAG due to its hydrophilic-hydrophobic balance.
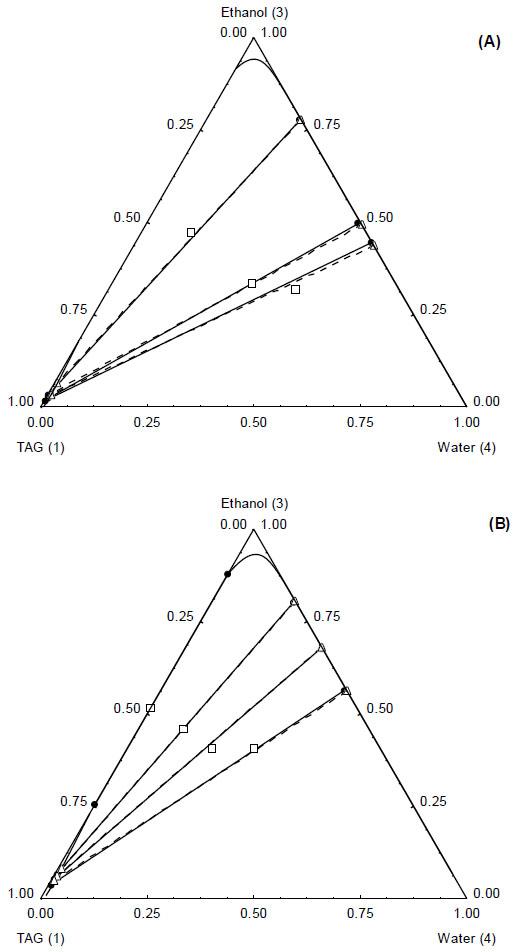
Ternary diagram for the system TAG(1) + ethanol(3) + water(4) at T = 298.15 K (A) and T = 328.2 K (B). Experimental ̶●̶, tie lines, □, overall composition), UNIQUAC model -Δ-, tie lines; ―, binodal).
The ternary system TAG + ethanol + water presented small miscibility regions. One occurs for high TAG concentration (above 75 wt%) associated to very small water concentration (below 0.5 wt%). The other miscibility region is obtained only for high ethanol concentrations (above 90 wt%).

Ternary diagram for the system TAG(1) + FFA(2) + ethanol(3) at T = 328.2 K. Experimental ̶●̶ , tie lines), UNIQUAC model -Δ-, tie lines, □, overall composition; ―, binodal).
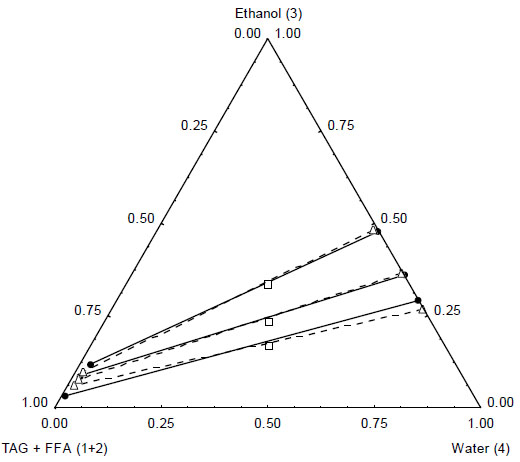
Ternary diagram for the system TAG + FFA(1+2) + ethanol(3) + water(4) at T = 328.2 K. Experimental ̶●̶ , tie lines, □, overall composition), UNIQUAC model -Δ- , tie lines). (Experimental data from Table 3)
CONCLUSION
This work reports liquid-liquid equilibrium data for olive oil TAG, FFA, ethanol and water systems, comprising results for ternary and quaternary systems at 298.2 and 328.2 K. The UNIQUAC model provides a very satisfactory representation of the experimental liquid-liquid equilibrium values for the highly non-ideal mixtures investigated. Hydroalcoholic systems containing FFA presented wider miscibility regions when compared to TAG. This was attributed to the presence of the polar carboxylic acid group in FFA, what makes then more hydrophilic when compared to TAG molecules. Results obtained in the present work might be valuable for process development, phase separation and optimization related to DAG-enrichment oil processes.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
The authors are grateful to PIBIC/CNPq, UFPR/TN, CNPq (Proc. No. 303573/2012-0) and Fundação Araucária-Paraná (Brazilian governmental agencies) for the financial and scholarships.


