All published articles of this journal are available on ScienceDirect.
Solubility of Acetophenone in Supercritical Carbon Dioxide
Abstract
The solubility data of acetophenone in supercritical carbon dioxide (scCO2) were measured using a static method at several temperatures (313.15, 323.15, 333.15, and 343.15K) and pressures ranging from10 MPa to 28 MPa. The density based models (Chrastil and Del valle– Aguilera models) and the Peng-Robinson equation of state (PR-EOS) with quadratic and Stryjek-Vera combining rules were employed to correlate the experimental data. Good correlations between the calculated and experimental solubility data were obtained. The sum of squared errors (SSE) are 0.38 % and 0.37 % for Chrastil and Del Valle – Aguilera models, respectively; and 9.07 % for Peng-Robinson equation of state with quadratic combining rule and 4.00 % for Peng-Robinson equation of state with Stryjek-Vera combining rule.
INTRODUCTION
In these recent years, the development of flavor and fragrance industries are remarkably fast due to the rapid development of food, cosmetics, and perfume industries. Thousands of new artificial flavor and fragrance compounds have also been produced to fulfill high demand for food, cosmetics, and perfume industries. However, artificial flavor and fragrance often create other problems in human health, and the concept “back to nature” becomes popular again. Different flavor substances can be found in natural products, and most of them have high economic value. One of them is acetophenone. Acetophenone is an aromatic ketone compound with the IUPAC name of 1-phenylethanone [1] and has a distinctive aroma. There are numbers of natural products contain acetophenone such as apple, apricot, banana, and cauliflower [2, 3].
The extraction process using organic solvent may be the most commonly used methods to obtain the acetophenone from natural products. However, this method possesses several disadvantages such as low purity and requires several stages of purification of the resulting product [4]. Extraction using supercritical CO2 is one of viable alternatives that can be used in aroma and fragrance industries. The working procedures are relatively straightforward and produce high extraction yields with high purity, and shorter extraction time [4]. Another advantage of using supercritical fluid is the elimination of subsequent separation processes such as distillation and crystallization. For the design of the supercritical extraction process of acetophenone from the natural matrices, the equilibrium or solubility data of acetophenone-supercritical CO2 is needed. Currently, several literatures [5, 6] report the solubility of acetophenone in supercritical carbon dioxide. Bamberger and Maurer [5] studied the solubility several aromatic hydrocarbons including acetophenone in supercritical carbon dioxide using a flow type apparatus.
The determination of the solubility of aromatic hydrocarbons in supercritical carbon dioxide was conducted gravimetrically. The measurements were performed at temperatures between 313 K and 393 K at pressures up to 18 MPa. Recently, Gumerov et al. [6] used the supercritical CO2 to extract several hydrocarbons and molybdenum from waste of propylene epoxidation process. They used dynamic flow method to extract and to obtain the solubility those hydrocarbons, and one of the hydrocarbons was acetophenone. Since all of the previous studies emphasized on the dynamic system, in the current study we focused on the combination of static system and gravimetrically method. Therefore, one of the objectives of this study is to obtain the solubility data of acetophenone on supercritical carbon dioxide at various pressures and temperatures.
To obtain the solubility data of compounds in the supercritical fluid (SCF) in a wide range of pressures and temperatures, is tedious, expensive, and time consuming work. In most cases, the data obtained from the experiments usually only valid in a narrow range of pressures and temperatures. To overcome this problem, usually a mathematical model which valid for a wide range of pressures and concentrations is needed. This mathematical model is usually developed from the limiting number of experimental data. In this paper, we employed density based models (Chrastil and Del Valle – Aguilera) and equation of state (EoS) approach (Peng-Robinson) to correlate the experimental solubility data of acetophenone in supercritical carbon dioxide. The solubilities of acetophenone in supercritical carbon dioxide were measured at four different temperatures (313.15, 323.15, 333.15, and 343.15) K and in the pressures range from (10 to 28) MPa.
MATERIAL AND METHODS
Material
Acetophenone (C8H8O) is a yellow liquid with a boiling point of 475.55 K [3]. Acetophenone used in this study was obtained as analytical standard and supplied by Sigma-Aldrich (CAS no: 98-86-2) with a purity of ≥ 98 %, and was used without any further purification. Food grade carbon dioxide with the purity of 99.9% was supplied by Aneka Gas Pty Ltd. Analytical grade ethanol was used to dissolve the acetophenone in the sample collector.
Experimental Procedure
Fig. (1) provides the schematic diagram of supercritical apparatus used in the current study. The main parts of the equipment consist of an Eldex high pressure pump (AA-100-S-2-CE, USA), Druck PTX 611 (USA) as a pressure transducer and Druck DPI 280 (USA) used as digital pressure indicator. The pressure accuracy during the experiment was within ± 0.01 MPa. In order to control and maintain the temperature, oven memmert (Germany) was used. The temperature accuracy during the experiment was within ± 1 K. Another part of the system was equilibration column (Swagelok, USA). The entire components, fittings, and tubing used in the system were made of stainless steel (Swagelok, USA). The maximum working pressure and temperature of the supercritical system was 30 MPa and 373.15 K, respectively.
The solubility of acetophenone in supercritical CO2 was obtained in the static mode. Brief descriptions of the experimental procedure are described as follow [7]: a known amount of acetophenone was loaded into the sample holder and then attached to equilibration column. The oven was turned on, and the system was heated until the desired temperature was reached (313.15, 323.15, 333.15, and 343.15 K). After the thermal equilibrium condition had been reached, the liquid CO2 was pumped to the equilibration column using a high pressure pump. Since the static method was used in this study, during the processes, valves V-2 was closed, while valves V-1 was kept open. After the equilibrium condition had been achieved, then the sampling tube was disconnected from the system by closing valve V-1. The sample in the sampling tube was released by opening valve V-2 to the collector containing a known amount of ethanol to fully separate acetophenone and carbon dioxide.
At least three replicated samples were taken at the experimental condition, and equilibrium composition was determined by averaging the replications. The overall error of each measurement was within 2 - 3 %. The concentration of acetophenone in ethanol was determined by means of a Shimadzu gas chromatograph (GC) provided with a flame ionization detector. Gas chromatography was calibrated externally using acetophenone solutions with different concentrations. The uncertainty of the GC measurement was ± 0.1 mg.L-1.
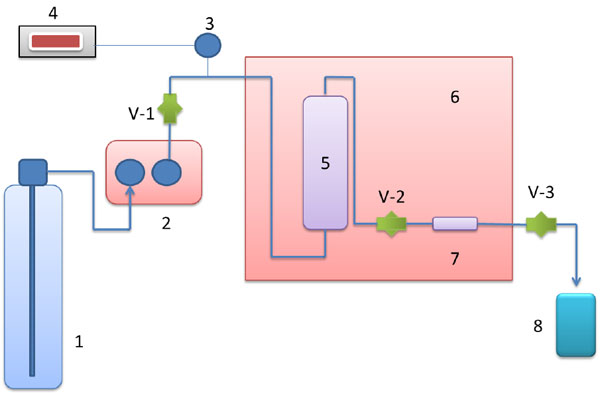
Schematic diagram of supercritical apparatus. 1. Liquid CO2 cylinder; 2. High pressure pump; 3. Pressure transducer; 4. Digital pressure indicator; 5. Equilibration column; 6. Oven; 7. Sampling tube; 8. Sample collector.
The operational conditions for GC are described as follows: (1) column: DB Wax; (2) oven: 40°C for 5 minutes; 40°C-230°C with ∆T = 10°C/minute; 230°C for 7 minutes; (3) carrier gas: helium at 34 cm/s; (4) injector: split 1:10, 250°C; and (5) injector: FID, 300°C.
RESULTS AND DISCUSSIONS
The solubilities of acetophenone in supercritical CO2 were measured at temperatures ranging from 313.15 to 343.15 K and pressure from 10 MPa to 28 MPa. The experimental solubility data of acetophenone in supercritical carbon dioxide are given in Table 1 and also plotted in Fig. (2). The densities of carbon dioxide at several pressures and temperatures were predicted using Stryjek and Vera modification of the Peng-Robinson equation of state [8], and the results are presented in Table 1.
Experimental data of the solubility of acetophenone in supercritical carbon dioxide.
| T/K | P/MPa | ρCO2/g.L-1 | 104.y2* |
|---|---|---|---|
| 313.15 | 10 | 565 | 0.88 |
| 12 | 667 | 1.07 | |
| 14 | 726 | 1.20 | |
| 16 | 768 | 1.30 | |
| 18 | 802 | 1.38 | |
| 20 | 830 | 1.43 | |
| 22 | 855 | 1.48 | |
| 24 | 876 | 1.51 | |
| 26 | 895 | 1.53 | |
| 28 | 913 | 1.53 | |
| 323.15 | 10 | 376 | 0.81 |
| 12 | 535 | 1.11 | |
| 14 | 625 | 1.26 | |
| 16 | 684 | 1.38 | |
| 18 | 728 | 1.46 | |
| 20 | 764 | 1.55 | |
| 22 | 794 | 1.59 | |
| 24 | 819 | 1.64 | |
| 26 | 842 | 1.67 | |
| 28 | 862 | 1.69 | |
| 333.15 | 10 | 293 | 0.62 |
| 12 | 415 | 0.99 | |
| 14 | 521 | 1.30 | |
| 16 | 596 | 1.47 | |
| 18 | 652 | 1.58 | |
| 20 | 695 | 1.69 | |
| 22 | 731 | 1.78 | |
| 24 | 761 | 1.85 | |
| 26 | 787 | 1.88 | |
| 28 | 811 | 1.89 | |
| 343.15 | 10 | 251 | 0.38 |
| 12 | 342 | 0.80 | |
| 14 | 435 | 1.15 | |
| 16 | 514 | 1.51 | |
| 18 | 577 | 1.76 | |
| 20 | 627 | 1.93 | |
| 22 | 668 | 2.05 | |
| 24 | 703 | 2.11 | |
| 26 | 733 | 2.13 | |
| 28 | 759 | 2.14 |
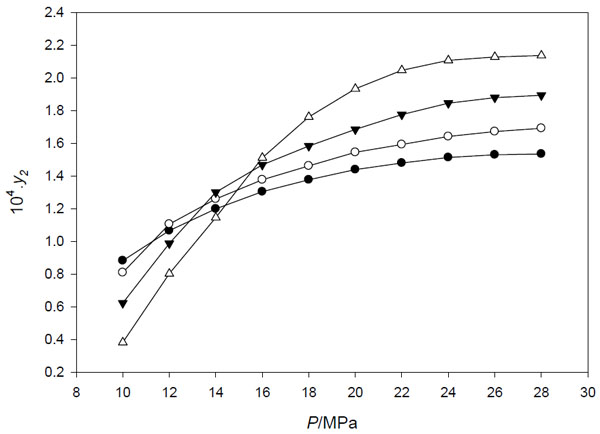
Experimental solubility of acetophenone in supercritical CO2 as a function of pressure at different temperatures: ●, 313.15 K; ○, 323.15 K; ▼, 333.15 K; ∆, 343.15 K..
Peng Robinson equation of state with Stryjek-Vera modification has the form as follows:
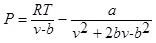 |
(1) |
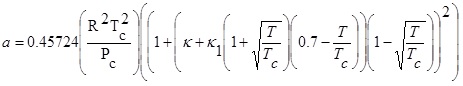 |
(2) |
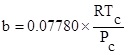 |
(3) |
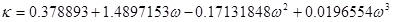 |
(4) |
Where P and V are pressure and molar volume, respectively, R is the gas constant; Tc and Pc are the critical temperature and critical pressure of the pure component, respectively. The ω is the acentric factor, k1 is an adjustable parameter characteristic of each pure compound, which for the supercritical region, 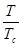 ≥ 1, the use k1 = 0 is recommended for all compounds [8].
≥ 1, the use k1 = 0 is recommended for all compounds [8].
From the experimental data shown in Fig. (2), it is clear that at constant temperature, the solubility of acetophenone increases with increases of pressure. This phenomenon can be explained by the effect of the solvent density on the solubility of the solute at supercritical condition: as the pressure increases, the carbon dioxide density also increases leading to the increases of the strength of the solvent and enhances the solute solubility.
The solubility data of acetophenone in supercritical CO2 (expressed in mole fraction) are ranging from 0.38 × 10-4 at a temperature of 343.15 K and a pressure of 10 MPa to 2.14 × 10-4 at a temperature of 343.14 K and a pressure of 28 MPa. Fig. (2) indicates the presence of the crossover region. Below crossover region, the solubility of acetophenone in supercritical carbon dioxide decreases with increasing temperature, but above the crossover region, the opposite phenomenon is observed. The crossover region was observed at a pressure range between 11 and 16 MPa. This phenomenon can be explained by two crucial factors (density of the SCF and the solute vapor pressure) which affected by the change of temperature. As the temperature increases, the density of SCF decreases but the solute vapor pressure increases. These two factors have the tendency of opposite effects on the solubility curve. The effect of density seems to be dominant in the low pressure region and cause the decrease of the solute solubility as the temperature increases, while, the solute vapor pressure seems to be dominant in the high pressure region hence the solute solubility increased as the temperature increases [9-11].
Density Based Models
The density-based equations, are the most widely used models to correlate the solubility of various compounds in supercritical fluids, due to its simplicity and do not require any critical physical properties. The earliest known of the density based model was developed by Chrastil [12] in 1982. He developed the model based on the theory of the solvato complex formation (in equilibrium, one molecule of solute A associates with k molecules of solvent B to form a solvato complex ABk). His semiempirical model has the mathematical form as follows:
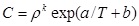 |
(5) |
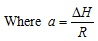 |
(6) |
∆H is the sum of heat of vaporization and solvation of the solute and R is the gas constant (8.3145 J.mol-1.K-1).
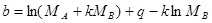 |
(7) |
C is the solubility of solute in a gas (g/L), ρ is the density of the gas (g/L), k is the association number, T is temperature (K), MA and MB are the molecular weights of the solute and the gas, respectively, q is a constant, a and b are two equation parameters defined in Eqs. (6) and (7), respectively [12].
Parameter a is a constant, which depends on the heat of vaporization and solvation enthalpies of the solute. Parameter b is a function of the association number and the molecular weights of the solute and supercritical fluids. This parameter is not affected by changing of temperature [12].
In order to obtain the parameters k, a, and b, the fitting of the solubility experimental data was conducted for all temperatures simultaneously using a nonlinear least square method by minimizing the following sum of squared errors as the objective function.
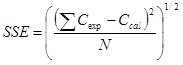 |
(8) |
Where Cexp is the experimental solubility of acetophenone in supercritical CO2, Ccal is the calculated solubility, and N is the number of experimental data. Table 2 represents the fitting parameters values and the sum of squared errors of Chrastil equation.
Optimized parameters of chrastil model for CO2(1) + acetophenone(2).
| k | a | b | SSE (%) |
| 2.0086 | -1965 | -8.3811 | 0.38 |
Table 2 and Fig. (3) show that the Chrastil equation can represent the experimental solubility data of acetophenone in supercritical CO2 exceptionally well. The sum of the squared error value of the data fitting is 0.38, indicates a good consistency of the Chrastil model with the experimental data.

Chrastil plot of acetophenone solubility in scCO2 as a function of temperature and density.
From the value of parameter a in the Table 2, the total enthalpies of vaporization and solvation of the solute can be estimated to be -16.33 kJ.mol-1. The negative value of the parameter a means that the associating process is an endothermic process.
The value of association number k obtained from the fitting of data is 2.0086. It means that one molecule of acetophenone associates with 2.0086 molecules of carbon dioxide to form a solvato complex in supercritical condition.
As mentioned before, the advantages of using Chrastil equation are the model does not require any physical-chemical property data of the solute [13] and its simple form. Therefore, this equation is applicable in most cases.
Del Valle and Aguilera [14] proposed a modified expression of the Chrastil’s equation in the form of:
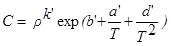 |
(9) |
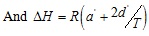 |
(10) |
Where ∆H refers to the sum of the heat of vaporization and solvation of the solute. The parameter d’ is associated with the change in heat of vaporization and the other parameters and variables are the same as previously explained for Eq. (5). This equation can fit the experimental data well as shown in Fig. (4). The parameters obtained from the fitting experimental data are given in Table 3.
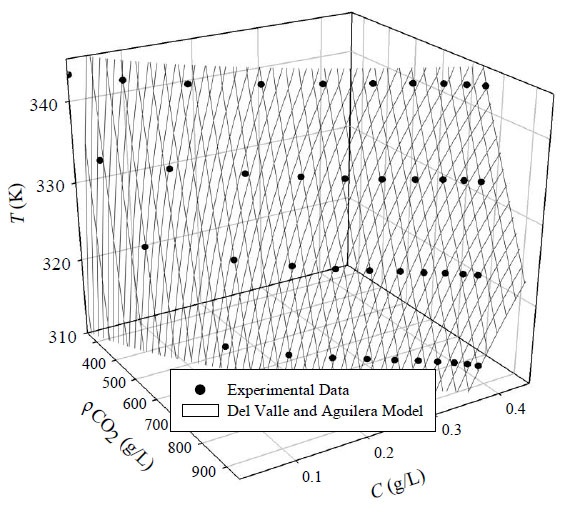
Del valle and aguilera plot of acetophenone solubility in scCO2 as a function of temperature and density.
Optimized parameters of del valle and aguilera model for CO2(1) + acetophenone(2).
| k | a' | b' | d' | SSE (%) |
| 2.0135 | -12686 | 7.9447 | 1754521 | 0.37 |
From the value of the parameter a’ and d’ in the Table 3, with Eq. (10), the average of total enthalpies of vaporization and solvation of the solute can be estimated to be -16.46 kJ.mol-1. The negative value of the parameter a means that the associating process is an endothermic process.
The value of association number k obtained is 2.0135. That means one molecule of acetophenone associates with 2.0135 molecules of carbon dioxide to form a solvato complex in supercritical condition. Since Del Valle and Aguilera model was developed based on the Chrastil model, therefore, the value of the parameter k in this model is similar to the Chrastil equation. Del Valle-Aguilera model is a modification of Chrastil model with addition one parameter in order to consider the impact of changing temperature.
Table 3 and Fig. (4) show that Del Valle and Aguilera equation can represent the experimental solubility data of acetophenone in supercritical CO2 exceptionally well. The sum of squared errors percentage of the data is 0.37. It shows a significant consistency of this model with the experimental data.
Equation of State Model
In this paper, the experimental solubility data of acetophenone in the supercritical CO2 were also correlated using an equation of state. The equation of state used here is Peng-Robinson EoS with the form as described in Eq. (1). The pure component parameters (Tc, Pc, and ω) for the solute were calculated using Joback and Lee-Kesler methods and the results are summarized in Table 4.
The pure component parameters for peng-robinson EoS.
| Compound | Tc(K) | Pc(bar) | ω |
| Acetophenone | 714 | 40.6 | 0.354 |
| CO2 | 304.15 | 73.8 | 0.225 |
For a multicomponent mixture, the parameters a and b in Peng-Robinson can be correlated using Van der Waals mixing rules:
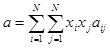 |
(11) |
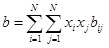 |
(12) |
To calculate the values of aij and bij, a combining rule was needed. The classical quadratic [15] combining rule for the parameters aij and bij have the following form:
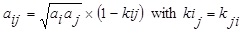 |
(13) |
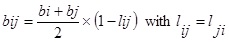 |
(14) |
Where ai and aj are the Peng-Robinson parameters for pure component i and j calculated from
Eq. (2). While bi and bj are obtained from Eq. (3). One such combining rule also has been proposed previously by Stryjek and Vera [16] for the parameters aij and bij which have the following form:
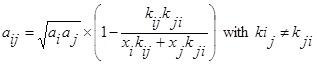 |
(15) |
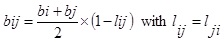 |
(16) |
Where kij, kji, and lij are the binary interaction parameters and obtained by fitting the experimental data; xi and xj are the solute and solvent mole fraction, respectively.
Fig. (5) depicts the predicted solubility of acetophenone in supercritical carbon dioxide using quadratic combining rule. The binary interactions obtained from the fitting are summarized in Table 5. The parameter kij is found to increase with increasing temperature. However, the parameter lij does not have the dependency with temperature, as can be seen the inconsistency of its trend with temperature.
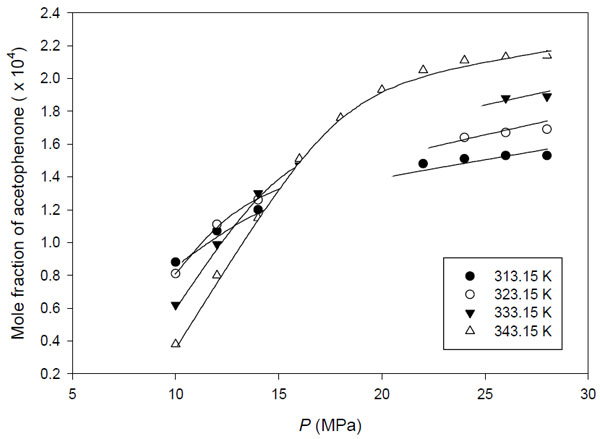
Correlation of the experimental solubility data of acetophenone using peng-robinson EoS with quadratic combining rule.
Table 6 and Fig. (6) represent the predicted solubility of acetophenone in supercritical carbon dioxide using the Stryjek-Vera combining rule. It can be seen that the Peng-Robinson EoS with the Stryjek-Vera combining rule correlate the experimental data fairly well with the average sum of squared errors percentage about 4%. It can be seen from Table 6 that the value of kij is found to decrease with increasing temperature. However, the parameters kji and lij do not have the consistent trend with temperature, and may be considered essentially constant because it has a small change with temperature. The Peng-Robinson EoS with Stryjek-Vera combining rule describes the experimental data better than PR EoS with quadratic combining rules for acetophenone-supercritical CO2 systems, as seen in Tables 5 and 6.
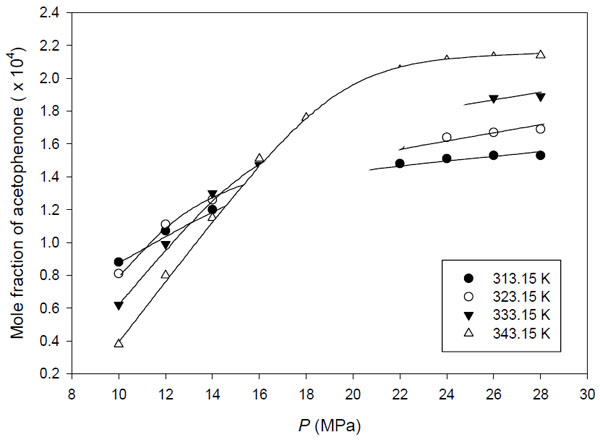
Correlation of the experimental solubility data of acetophenone using peng-robinson EOS with stryjek-vera combining rule.
The binary interaction parameters obtained, kij and lij, account for the solute-solvent energetic interactions and size and shape differences, respectively. Change of temperature and pressure essentially not affected to the binary interaction parameter kij and lij. Therefore, these parameters may be used directly to predict the solubility at other temperatures by using the Peng-Robinson Equation of State model [17].
Optimized parameters of peng-robinson equation of state with quadratic mixing rule for CO2(1) + acetophenone(2).
| T(K) | kij | lij | SSE (%) |
| 313.15 | 0.099967 | 0.034190 | 6.76 |
| 323.15 | 0.099981 | 0.029516 | 12.63 |
| 333.15 | 0.117338 | 0.041413 | 5.52 |
| 343.15 | 0.117992 | 0.029246 | 11.37 |
Mixing rule for CO2(1) + acetophenone(2).
| T (K) | kij | lij | kji | SSE (%) |
| 313.15 | 0.119969 | 0.034190 | 0.099993 | 3.44 |
| 323.15 | 0.114434 | 0.029516 | 0.099991 | 5.21 |
| 333.15 | 0.115358 | 0.041413 | 0.099963 | 2.57 |
| 343.15 | 0.109189 | 0.029246 | 0.099972 | 4.79 |
CONCLUSION
Solubility data of acetophenone in supercritical carbon dioxide at various pressure and temperature were obtained in this study. The solubility data were correlated using density based correlations (Chrastil model and Del Valle-Aguilera model) and Peng-Robinson EoS approach. Quadratic and Stryjek-Vera models were used as combining rules in correlating the experimental data with Peng-Robinson equation of state. The results shown that those models are able to correlate the solubility data of acetophenone in supercritical CO2.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTs
Thanks for the support of Marine public welfare industry research special funds project" Research and application of integrated submarine pipeline detection technology and risk assessment technology" (item number: 2013418026-3).


