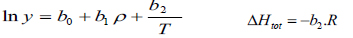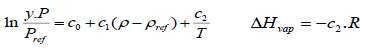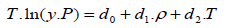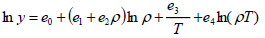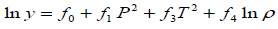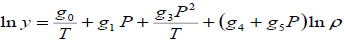All published articles of this journal are available on ScienceDirect.
Semi-Empirical Models and Cubic Equations of State for Correlation of Solids Solubility in scCO2: From Simple to Complex Substances
Abstract
The present paper examines the performance of cubic equations of state (CEoSs) and semi-empirical density-based models in correlating the solubility in supercritical carbon dioxide (scCO2) of several solid compounds of interest to the food industry, namely 2-propenamide, bixin, β-carotene and C-tetramethylcalix[4]resorcinarene. The four target solutes are with increasing structural complexity and, are typically pure solids, at ambient or slightly elevated temperatures.
The Soave-Kwong-Redlich (SRK) CEoS with the one-fluid van der Waals mixing rule was chosen as representative of the class of CEoSs, while the group of the density-based models includes Chrastil model, Kumar and Johnston model, Bartle et al. model, Méndez–Santiago and Teja model, Garlapati and Madras model, Nejad et al. model and Khansary et al. model.
The results obtained reveal that the more recently advocated density-based models (Garlapati and Madras, Nejad et al. and Khansary et al. models) perform better than the other models with overall average absolute deviations, AARD %, of 6.3, 7.8 and 7.2 %, respectively. The 9.1% overall AARD for the SRK CEoS was considered satisfactory since it can be used as a reliable thermodynamic model to predict the solubility of any compound for which there are no sufficient experimental data available.
1. INTRODUCTION
In recent years, supercritical fluid (SCF) technology has considerably outgrown its first modest applications and nowadays a substantial number of high added value substances of interest to the food, nutraceutical, pharmaceutical, cosmetic, body care and hygiene industries are produced using SCFs [1]. Supercritical carbon dioxide (scCO2) is the usual solvent of choice because it is non-flammable, non-explosive, cheap and easily accessible in high purity. Furthermore, its critical point (Tc = 31.1 ºC, Pc = 7.38 MPa) allows application of relatively low operation temperatures and thus the extracts of thermally labile solutes better resemble the natural material than the products of steam distillation and conventional extraction where the solvent is usually separated from the extract under increased temperature [2, 3].
The design, optimization and development of SCF technologies require a detailed knowledge of the phase behavior of the systems involved and, particularly, of the solubility of solutes in the high pressure solvent. The solutes of interest to the food industry are in their majority relatively non-volatile complex solids, and to correlate their solubility in scCO2 usually two groups of models are used: equations of state (EoSs) and semi-empirical equations.
There are many studies in the literature which analyze and compare the applicability of different EoSs, with different mixing rules, to correlate the solubility of solid solutes in scCO2, see for example the very recent works of Yazdizadeh et al. [4, 5], to mention just a few. Other researchers examined semi-empirical models and their performance in correlating the solubility of important compounds in scCO2 [6-9].
The focus of the present study is on performance comparison of cubic equations of state (CEoSs) and semi-empirical models in correlating the solubility of solid solutes in scCO2. As a representative of the EoSs models we have chosen the Soave-Redlich-Kwong cubic EoS (SRK CEoS) with the one-fluid van der Waals mixing rule. Seven density-based models are selected. Some of them, e.g. Chrastil model [10], are very well-established and widely used, while others like Khansary et al. model [9] are advocated quite recently.
The target compounds are solid solutes of interest to the food industry, namely 2-propenamide (acrylamide), bixin, β-carotene and C-tetramethylcalix[4]resorcinarene. The reason for choosing those particular compounds is two-fold: firstly they are representatives of substances with increasing size and complexity; secondly there are consistent and reliable experimental data available on their solubility in scCO2. Hereunder, a very brief summary of their basic characteristics and importance is given.
Acrylamide, a white crystalline solid, with suspected human carcinogen properties, has an amide bond, similar to the essential bond between amino acids in proteins. Furthermore, it has been found in various heat-processed foods [11], such as potato chips and bread. Moreover, the latest decisions and recommendations of the European Commission on the levels of acrylamide in food provide a solid impetus to examine this compound [12, 13].
Bixin is a carotenoid found only in the seeds of the tropical tree annatto (Bixa orellana). The seeds produce pigments that have widespread use in the food industry for coloring butter, margarine, cheese, oils, and sauces, with hues ranging from yellow to red [14]. Bixin is one of the main natural coloring materials that easily degrades when exposed to light but is less sensitive to heat (stable up to 125 °C) [15].
β-carotene is a carotenoid with colors ranging from light orange to dark red. It is largely distributed in plants (carrots, tomatoes, annatto, etc.), fungi and algae and has important applications as provitamin A, antioxidant, and coloring material [16].
C-tetramethylcalix[4]resorcinarene is a cyclic compound belonging to calixarenes group. Calixarenes are cavitands referred to as “molecular baskets” or “host-guest” molecules because they possess hydrophobic cavities that can hold smaller molecules or ions and can form inclusion complexes with many practical applications [17]. Knowledge of C-tetramethylcalix[4]resorcinarene solubility in scCO2 is extremely important in order to establish whether it can act as a co-solvent to scCO2 in an efficient environmentally friendly and benign new green route for in situ product removal of inhibitory bio-products, like organic acids and some antibiotics.
Some additional information on the four binary systems examined, namely number of points available, Np, temperature and pressure intervals and references to the studies where the respective experimental solubility data were presented, is given in (Table 1).
Details of the four binary systems examined and respective references.
The solubilities of acrylamide and C-tetramethylcalix[4]resorcinarenein scCO2 were experimentally measured and reported in the literature for the first time by the present authors and colleagues [18, 19]. The data obtained is completely reliable and consistent even for such difficult compounds with very low solubility as calyx[4]resorcinarenes [19].
Just few studies are devoted to the solubility of bixin in scCO2, e.g. [20-22]. The solubility of β-carotene in scCO2 was a topic of extensive research and considerable amount of data is available, [23-25] are just an example.
It should be noted that for substances exhibiting low – to very low solubility in scCO2 (e.g. β-carotene) there are some scatter and uncertainties associated with the experimental solubility data reported by the different laboratories. In view of this, the performance of the models chosen for correlating the solubility of bixin and β-carotene in scCO2 is examined on the basis of our experimental data only, [19, 20, 23] respectively.
In what follows we will first briefly discuss the framework, based on applying an EoS as the thermodynamic model, to correlate the experimental solubility of the four compounds. Then the seven semi-empirical density-based models used will be presented. The results obtained for the two groups of models will be given and a comparison of their performance will be made on the basis of percentage average absolute deviations, AARD %, calculated between the experimentally measured and correlated results. These numbers, however, don’t reveal in an explicit manner the difficulties, both informational and numerical, accompanying the application of EoSs. We will just mention the necessity to know the solid solute properties like critical and fusion properties, solid molar volume, etc. Frequently, some or the majority of these properties cannot be determined experimentally and hence have to be estimated, which, in its own turn, brings uncertainty and errors to the correlation results. On the other end are the density–based models which do not require any such data and hence their application is straight forward.
2. EQUATION OF STATE – THERMODYNAMIC MODELING FRAMEWORK
To correlate the solubility of solid solutes in scCO2 we apply the dense gas approach, which is based on the equifugacity condition for the solid solute. Thus, assuming an EoS model for the fluid phase and denoting by the superscript “S” the solid solute and by the superscript “F” the fluid phase the following holds:
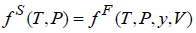 |
(1) |
where f S is the fugacity of the solute in the pure solid phase, f F is fugacity of the solute in the fluid phase solution, y = (y1, y2, …,yNc)T is the vector of the fluid phase mole fractions of the Nc components, and V is the molar volume of the fluid from an EoS model. Additional relationship that must be satisfied is summation to one of the fluid phase mole fractions.
Further, following McHugh et al. [26], the solid vapor pressure is used as the reference fugacity of the solid solute. Thus, the fugacity of a specific solid solute, i, is:
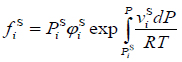 |
(2) |
where piS is the sublimation (vapor) pressure of the pure solid, φiF is its fugacity coefficient at sublimation pressure and Vsi is the molar volume of the solid, all at temperature T.
The fugacity of the solute in the fluid phase is:
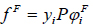 |
(3) |
where φFi is the fugacity coefficient, and γi is the solubility (mole fraction) of the solute in the supercritical fluid.
Assuming that the solid phase is pure, the fugacity of the solute in the solid state is equal to the pure solid fugacity, and then equation (2) can be rewritten as follows:
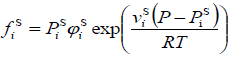 |
(4) |
Applying the thermodynamic equilibrium condition, the mole fraction of the solid component in the fluid phase can be expressed as:
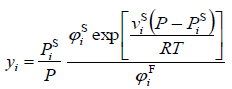 |
(5) |
In most practical cases φsi is nearly equal to unity because the sublimation pressure of the solid is quite small. However, φFi is always far removed from unity and the large solubility enhancements in SCFs relative to an ideal gas are a results mainly of the exceptionally small values of φFi.
The above equations set the dense gas approach thermodynamic modeling framework for correlating solid solubilities in SCFs. They show that the solute solubility is primarily a function of the solid solute pure compound physical properties, the system temperature and pressure, and the fugacity coefficient of the solid solute in the fluid mixture, which is calculated by a thermodynamic model.
2.1. Thermodynamic Model
Cubic EoSs are exceedingly simple and have been remarkably successful in modeling SCF-phase behavior and are probably the most widely used in analyzing experimental data. Moreover, the cubic EoS must be the equation of choice for process design of complex systems like “solid+SC fluid”, because the interactions are too involved to justify the use of a more fundamentally based equation [2].
If the SRK cubic EoS is written in terms of compressibility Z:
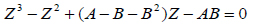 |
(6) |
then the expression for the fugacity coefficient of component i is:
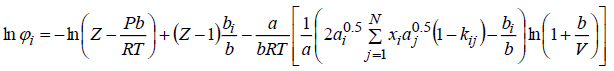 |
(7) |
where:
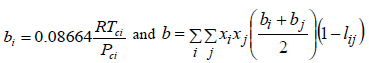 |
(8) |
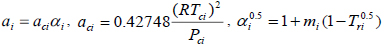 |
(9) |
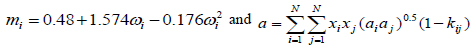 |
(10) |
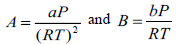 |
(11) |
In this study we use the one-parameter-per-pair (1PWDW) version of the van der Waals one fluid mixing rule to calculate the fugacity coefficient of the solid solute and hence the expression for the cross-co-volume parameter, equation (8), is now, respectively:
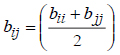 |
(12) |
2.2. Pure Component Properties – Measurement and Estimation
The four systems that we focus on involve small-, medium- and large-sized solutes at ambient or slightly elevated temperatures where they are typically pure solids. The increasing complexity of these substances is demonstrated by their polyfunctionality (two or more functional groups); multiple molecular conformations; complex molecular interactions, such as large dipoles, high polarizability, hydrogen bonding, and charge-transfer complexes. Moreover, bixin and β-carotene can degrade when exposed to light and are sensitive to heat, while acrylamide can polymerize, which makes it almost impossible to obtain experimentally some of their thermophysical properties.
The two groups of properties required for modeling the solubility of the target compounds in scCO2 are their critical parameters and melting properties. As it has been mentioned previously, the amounts of reliable measured thermophysical properties data are extremely limited. Thus, correlation of solubility requires not only robust thermodynamic models but also reliable methods to estimate the values of the missing thermophysical properties as inaccuracies in the latter influence in a major way the quality of phase equilibria predictions and correlations, which in their own right, have a major impact on the modelling and design of SCF processes.
Herewith, we briefly summarize the availability of data:
Acrylamide:For this small molar mass compound the only experimentally available properties are its melting temperature and enthalpy of fusion [27], hence its critical properties and sublimation pressures at the temperatures of interest to the experiment have to be estimated.
Bixin is a carotenoid compound of a molecular weight 394.0 g/mol. Chemically it is a monomethyl ester of the dicarboxylic acid norbixin [28]. The only experimentally available information is its melting temperature. Still, some of its properties have been estimated and reported in the literature, applying for example the Joback’s method [16]. Further, in an attempt to achieve a better representation of the experimental data, bixin critical properties and sublimation pressures were estimated minimizing the deviations between the calculated and the experimental binary data [16].
β-carotene is a carotenoid compound of high molecular weight, 536.9 g/mol. The data available in the literature for β-carotene include its melting temperature and enthalpy of fusion. In their paper Cygnarowicz et al. [29] cited the work of Bruno, who had reported several vapor pressure measurements for β-carotene, with 10-14 bar as an upper bound at 303.2 K. Nobre et al. [16], in analogy with bixin, have used β-carotene’s critical properties and sublimation pressures as minimization parameters and reported values of the order of 10-14 to 10-16 bar for the latter.
Pure component thermophysical properties of the four target solid solutes.
| Thermophysical Properties | Acrylamide (C3H5NO) | Bixin (C25H30O4) | β-carotene (C40H56) | C-tetramethylcalix[4]Resorcinarene (C32H32O8) |
|---|---|---|---|---|
| Molar mass g/mol | 71.08 | 394.0 | 536.9 | 544.59 |
| pc/bar | 57.3 | 9.64 | 5.48 | 0.701 |
| Tc/K | 776 | 907.77 | 1041.9 | 1158.4 |
| VS/cm3×mol-1 | 63.35a | 383.7 | 536.5b | 448.86 |
| ∆Hfus/J×mol-1 | 15330a | 31540 | 56000a | 48388d |
| Tm/K | 357.65a | 471.15c | 456a | 605.65d |
| Pssubl/MPa at T=308.2 K | 1.896E-6 | - | - | - |
| Pssubl/MPa at T=313.2 K | 3.291E-6 | 3.89E-14 | 3.37E-14 | 2.21E-16 |
| Pssubl/MPa at T=323.2 K | 9.423E-6 | 5.43E-13 | 2.52E-13 | 1.14E-15 |
| Pssubl/MPa at T=333.2 K | - | 8.03E-12 | 5.16E-12 | 4.3E-15 |
C-tetramethylcalix[4]resorcinarene is a synthetic macrocyclic compound with molecular weight of 544.59 g/mol. Aside from the information that the melting point of this calixarene should be higher than 300 oC there are no other data available in the literature. The melting point was hence determined by DSC analysis using the Pyris software [19]. All other properties required should thus be estimated.
Hereunder the scenario applied by us to obtain values for the missing properties of the target compounds is briefly summarized:
The solid molar volumes (where data is not available) were estimated applying the method of Bondi [30]. The critical parameters were estimated applying the methods suggested in ref. [31, 32]. With regard to calix[4]resorcinarene it should be noted that as this compound is an oligomer it can be treated as a conventional component and hence the above methods are applicable to estimate its critical properties.
The enthalpy of fusion (where not available) was estimated applying the method of Jain [33]. The sublimation pressures at the temperatures of interest to the experiment were calculated integrating the Clayperon equation from the respective melting temperatures (assuming that the difference between the triple-point temperature and the normal melting temperature of a solid solute is negligible) and the triple point pressure pTP, and assuming further a negligible dependence of the sublimation enthalpy with respect to temperature.
The information on the thermophysical properties of the four target solid solutes is summarized in (Table 2).
Although the critical parameters for the four solids studied are hypothetical, still there should be an assessment made whether the values estimated are reasonable. Furthermore, as mentioned, the critical parameters and sublimation pressures of β-carotene and bixin were estimated previously and reported in [16, 24].
To access our estimations we apply the generalized semi-theoretical expression advocated in ref. [34] to evaluate the reliability of the critical properties values obtained, according to:
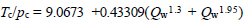 |
(13) |
where Tc is in Kelvin and pc is in bar. The dimensionless parameter Qw is a measure of the van der Waals molecular surface area and is calculated as the sum of the group area parameters, Qk:
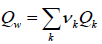 |
(14) |
where Vk is the number of times group k appears in the molecule. The group area parameters Qk are available in the UNIFAC tables.
For all four compounds the ratio of the values estimated by us gives a very good approximation to the theoretically calculated Tc/pc ratio; for β-carotene, for example, the theoretical Tc/pc is 198.9 versus ours 190.23.
3. SEMI-EMPIRICAL MODELS
To avoid the necessity of providing values for the thermophysical parameters of solids where they are not available, semi-empirical models to correlate the solubility can be employed as a viable alternative. Semi-empirical equations, like density-based models, do not require properties of the pure solid solute. They are based on error minimization technique and use several (3 to 6) parameters per compound to correlate its solubility at any pressure and temperature.
The density-based models applied in this study are summarized in Table 3, where a0, ..., a2, b0, …, b2, c0, … ,c2, d0, …, d2, e0, …, e2, f0, …, f4, and g0, …, g5 are adjustable parameters for the Chrastil [10], Kumar and Johnston [35], Bartle et al. [36], Méndez– Santiago and Teja [37], Garlapati and Madras [38], Nejad [39] and Khansary et al. [9] equations, respectively.
The first three equations are chosen because historically they were the first to be presented in the literature and are still widely used. Furthermore, some of their parameters can be associated with the total reaction heat (∆Htotal) or with solid properties like vaporization enthalpy (∆Hvap). Also, the equation of Méndez–Santiago and Teja [37], which is based on the theory of dilute solutions, was the first one to consider the effects of pressure directly and, hence, is widely applied to test the consistency of solubility data measured. Finally, the last three equations considered, namely [9, 38, 39], are more recent additions to the family of density-based models.
For the four solids examined, the parameters of each model were obtained by minimizing the percentage average absolute deviations, AARD% defined as:
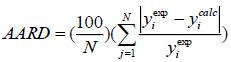 |
(15) |
where yiexp and yicale represent the experimental and correlated solubility (in mole fraction), respectively, of the solute in the supercritical solvent, and N is the number of data points. It should be noted, that other authors have suggested different objective functions, see for example [38]. Still, we apply equation (15) as it is one of the most widely used.
4. RESULTS AND DISCUSSION
4.1. Solubility Correlations Applying SRK CEoS
For the four target compounds, the unlike-pair temperature dependent interaction parameters, kij, of the SRK CEoS with the one fluid van der Waals mixing rule (1PWDW) were estimated by minimizing the difference between the experimental and calculated solubility data, applying a standard optimization procedure (Table 4). Needless to say that because of uncertainties in the values of the thermophysical properties estimated, the kij parameters might, to a certain extent, incorporate those possible errors.
The iterative numerical procedures employed to correlate the solubility of the four compounds are efficient and demonstrate steady convergence to the fixed point. The AARD % between the experimental and correlated solubilities is also given in (Table 4).
SRK CEoS: Binary interaction parameters (k ij ) and absolute average deviations (AARD) between the experimental and correlated solubilities at the respective temperatures , for the binary systems examined.
| T/K | Acrylamide+CO2 | Bixin+CO2 | β- carotene+CO2 | C-tetramethylcalix[4] resorcinarene+CO2 |
|---|---|---|---|---|
| kij AARD (%) | kij AARD (%) | kij AARD (%) | kij AARD (%) | |
| 308.2 | 0.1251 8.00 | --- --- | --- --- | --- --- |
| 313.2 | 0.1240 13.5 | 0.1365 13.54 | 0.1147 3.32 | 0.0833 7.54 |
| 323.2 | 0.1340 15.5 | 0.1413 4.38 | 0.1203 15.75 | 0.0915 6.83 |
| 333.2 | --- --- | 0.1488 5.42 | 0.1285 6.00 | 0.1070 9.12 |
It is worth mentioning that using the two interaction parameters (2PWDW) version of the van der Waals one fluid mixing rule did not lead to noticeable improvement of the correlative capabilities of the SRK EoS (in terms of AARD %) for the target compounds examined. A similar result for the AARD % from the experimental data available was reported by Yazdizadeh et al. [5] for some of the 23 industrial solid compounds investigated which solublities in scCO2 were correlated applying, among other models, the SRK CEoS with the 1PWDW and 2PWDW mixing rule, respectively.
There is no clear trend observed in the SRK CEoS performance for the four systems. Thus, the highest deviations (AARD of over 15 % at T = 323.2 K) are calculated for the solubility of the “simplest” compound, among the studied, acrylamide. This result is not totally unexpected as the disagreement between the experimentally measured and correlated solubilities at low temperatures and pressures for this compound is very high. Thus, if data below the cross-over pressure is excluded, the AARD % for acrylamide will be lower.
4.2. Solubility Correlations Applying Semi-Empirical Density Based Models
The application of the density-based equations to correlate the solubility of the four target compounds is completely straightforward taking into consideration that no information about the solid solutes’ properties is required. The models’ parameters and the AARD % between the experimental and correlated solubilities obtained, for each of the binaries, are presented in Tables 5 and 6, respectively. The order of the best performing models for correlating the solubility of the four compounds can change slightly from binary to binary.
| SN | Chrastil [10] | Kumar and Johnston [35] | Bartle et al. [36] | Mendez-Santiago and Teja [37] |
| ACR | a0 = -11.141 | b0 = 3.628 | c0 = 17.063 | d0 = -8334.55 |
| a1 = 2.591 | b1 = 3.860E-3 | c1 = 7.459E-2 | d1 = 2.338 | |
| a2 = -4179.75 | b2 = -4373.96 | c2 = -6190.82 | d2 = 18.682 | |
| AARD(%) = 7.34 | AARD(%) = 6.86 | AARD(%) = 13.80 | AARD(%) = 12.77 | |
| BIX | a0 = -55.543 | b0 = 0.847 | c0 = 20.232 | d0 = -15124.1 |
| a1 = 9.620 | b1 = 1.273E-2 | c1 = 1.649E-2 | d1 = 5.244 | |
| a2 = -8291.35 | b2 = -9044.25 | c2 = -10797.26 | d2 = 22.288 | |
| AARD(%) = 6.77 | AARD(%) = 7.55 | AARD(%) = 6.51 | AARD(%) = 6.62 | |
| CAR | a0 = -46.564 | b0 = 8.067 | c0 = 29.487 | d0 = -17728.0 |
| a1 = 9.708 | b1 = 1.445E-2 | c1 = 1.697E-2 | d1 = 5.552 | |
| a2 = 10860.80 | b2 = -11298.9 | c2 = -13288.37 | d2 = 31.153 | |
| AARD(%) = 7.19 | AARD(%) = 17.32 | AARD(%) = 11.08 | AARD(%) = 13.42 | |
| TET | a0 = -8.5464 | b0 = 3.347 | c0 = 18.546 | d0 = -10557.9 |
| a1 = 2.310 | b1 = 3.740E-3 | c1 = 7.142E-2 | d1 = 2.364 | |
| a2 = -6336.47 | b2 = -6161.39 | c2 = -8590.43 | d2 = 19.491 | |
| AARD(%) = 9.35 | AARD(%) = 10.59 | AARD(%) = 11.08 | AARD(%) = 9.71 |
However, it is demonstrated that overall the more recent models perform better, namely the Garlapati and Madras [38] and Khansary et al. [9] equations are at the top of the list. Probably, their success is due in part to the fact that both equations have five adjustable parameters which improves their flexibility. Still, in all cases studied the Chrastil model [10], with just three parameters, presents very adequate correlations when compared to the other equations.
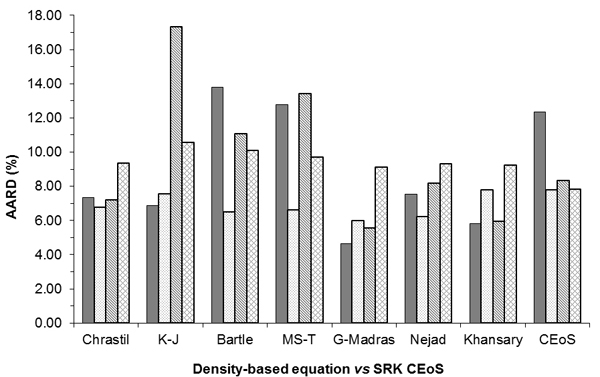
Semi-empirical density-based equations used in this study to correlate the solubility of
solid solutes in scCO2 comparison with the SRK CEoS.
 Acrylamide+CO2;
Acrylamide+CO2;
 bixin+CO2;
bixin+CO2;
 β-carotene+CO2 and
β-carotene+CO2 and
 C-tetramethylcalix[4]resorcinarene+CO2.
C-tetramethylcalix[4]resorcinarene+CO2.
The total heat of reaction, ∆Htot, of the four compounds was determined and the respective values are presented in (Table 7). As seen, there is a very good agreement between ∆Htot obtained by the Chrastil and the K-J model. The heat of vaporization of the pure solutes, ∆Hvap , is estimated from the coefficients of the Bartle model and the respective values are also shown in (Table 7). As the ∆Hvap values for all four compounds are higher than those of the total reaction heat a conclusion can be made that the respective processes are endothermic.
Solvation heats, ∆Hsol, presented in Table 7, are obtained from the difference between the total reaction and vaporization heat. The values of ∆Hsol increase from acrylamide to C-tetramethylcalix[4]resorcinarene and are an indication of the significant intermolecular interactions that take place between the respective compounds and the CO2 in the fluid phase [6].
Moreover, the original parameter k in the Chrastil equation [10], which in our nomenclature is denoted by a1, is the association number that describes the number of scCO2 molecules in the solvated complex. In the cases studied, a1 increases from acrylamide to β-carotene, which reflects the increasing complexity of the solids examined. Still, for C-tetramethylcalix[4]resorcinarene, apparently the most complex of the four compounds, a1 value is about four times smaller than that for β-carotene and commensurable with that of acrylamide. Perhaps the properties of calyx[4]arene as a “host-guest” molecule can, to some extent, explain that.
It should be taken into consideration, however, that the relation of Chrastil equation a1 parameter with the number of scCO2 molecules in the solvated complex is neither straightforward nor is always applicable. For example, Coelho et al. [40], who measured and correlated the solubility of three representatives of anthraquinone dyes in scCO2, demonstrated that for those solids the increase or decrease of Chrastil a1 parameter can’t be connected directly to either the “complexity” or molecule size of the compounds examined.
| SN | Garlapati and Madras[38] | Nejad et al. [39] | Khansary et al.[9] |
| ACR | e0 = 3247.78 | f0 = -30.444 | g0 = -4508.14 |
| e1 = 482.32 | f1 = 5.107E-7 | g1 = -7.468E-2 | |
| e2 = -8291.35 | f2 = 6.768E-05 | g2 = -3.567E-3 | |
| e3 = -156221.0 | f3 = 2.480 | g3 = 1.0118 | |
| e4 = -481.18 | g4 = 1.181E-2 | ||
| AARD (%) = 4.65 | AARD (%) = 7.53 | AARD (%) = 5.80 | |
| BIX | e0 = -821.19 | f0 = -93.798 | g0 = -10939.0 |
| e1 = -107.40 | f1 = 5.838E-07 | g1 = -0.34098 | |
| e2 = 3.990E-4 | f2 = 1.230E-4 | g2 = -1.473E-2 | |
| e3 = 28644.5 | f3 = 9.576 | g3 = 2.3373 | |
| e4 = 114.86 | g4 = 5.340E-2 | ||
| AARD (%) = 5.98 | AARD (%) = 6.25 | AARD (%) = 7.79 | |
| CAR | e0 = 1673.70 | f0 = -97.826 | g0 = -15747.2 |
| e1 = 264.95 | f1 = -1.726E-06 | g1 = -0.36786 | |
| e2 = -1.805E-4 | f2 = 1.621E-4 | g2 = -8.440E-3 | |
| e3 = -92791.9 | f3 = 9.822 | g3 = 5.1644 | |
| e4 = -254.51 | g4 = 5.517E-2 | ||
| AARD (%) = 5.56 | AARD (%) = 8.19 | AARD (%) = 5.94 | |
| TET | e0 = -229.05 | f0 = -37.977 | g0 = -7703.90 |
| e1 = -28.731 | f1 = -6.603-07 | g1 = -7.995E-2 | |
| e2 = -1.746E-4 | f2 = 9.206E-05 | g2 = 2.143E-3 | |
| e3 = 4321.89 | f3 = 2.343 | g3 = 1.8190 | |
| e4 = 31.771 | g4 = 1.103E-2 | ||
| AARD (%) = 9.13 | AARD(%) = 9.32 | AARD (%) = 9.25 |
The correlation results for the solubility of several statin drugs in scCO2 [6], as well as those for 27 pharmaceutical compounds presented in [7] are just two more such examples.
The performance comparison, in terms of AARD %, between the SRK CEoS and the seven semi-empirical equations, is shown on Fig. (1).
CONCLUSION
In general, the results obtained demonstrate that the SRK EoS not only captures and reproduces quite well the qualitative patterns of the solubility behavior of the target compounds studied but also gives an acceptable quantitative agreement with the experimental data. The agreement can be even further improved if some of the thermophysical parameters were not estimated but accepted as adjustable parameters. For example, it is well-known that the sublimation pressure plays a dominant role in the correlation of solubility data and hence, in many cases, when such values for the compound of interest are not available experimentally, researchers tend to treat sublimation pressure as an adjustable parameter. Needless to say, that this will further complicate the calculations.
Total heat of reaction, vaporization and solvation calculated in this study for the four solids.
| Compound | ∆Hatot(kJ mol-1) | ∆Hbtot(kJ mol-1) | ∆Hcvap(kJ mol-1) | ∆Hdsol(kJ mol-1) |
|---|---|---|---|---|
| Acrylamid | 34.75 | 36.37 | 51.47 | 15.91 |
| Bixin | 68.93 | 75.19 | 89.77 | 17.70 |
| β-carotene | 90.30 | 93.92 | 110.48 | 18.37 |
| C-tetramethylcalix[4]resorcinarene | 51.56 | 51.31 | 71.42 | 19.98 |
Finally, it should be underlined that though more complex in nature and application demanding, CEoSs can be used to predict the solubility of any compound for which there are not sufficient experimental (or not at all) data available, while the availability of enough data is an absolute prerequisite for the application of the semi-empirical density based models.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
The authors are thankful for the financial support from the Bulgarian Science Fund, Ministry of Education and Science (CONTRACT GRANT No: B01/23) and to FCT - Fundação para a Ciência e Tecnologia, projects UID/QUI/00100/2013 and UID/ECI/04028/2013.