All published articles of this journal are available on ScienceDirect.
Parameter Identification in Liquid-Liquid Equilibrium Modeling of Food-Related Thermodynamic Systems Using Flower Pollination Algorithms
Abstract
In this paper, the liquid–liquid equilibrium of twenty two ternary and quaternary systems relevant for food industry was modeled using the NRTL and UNIQUAC equations and the Flower Pollination Algorithm (FPA). FPA is an emerging nature-inspired stochastic global optimization method and it has been used for LLE parameter identification of local composition models in multicomponent mixtures. FPA and its modified version (MFPA) were assessed for solving LLE parameter estimation problems in several systems relevant for food industry. Thenumerical performance of these stochastic methods has been analyzed at different numerical scenarios with and without the application of closure equations. Results showed that MFPA outperformed FPA and other metaheuristics (e.g., Simulated Annealing, Genetic Algorithm and Harmony Search) for LLE parameter identification in local compositions models. MFPA with closure equations is a reliable approach for determining the best interaction parameter of NRTL and UNIQUAC models in the LLE data processing of food-related thermodynamic systems.
1. INTRODUCTION
Liquid-liquid equilibrium (LLE) data are essential for the proper design in the food products industry [1, 2]. For instance, the solvent extraction is a LLE-based process commonly used in this sector, which is an environmentally friendly operation that needs less energy and produces minor environmental pollution than other separation schemes [1, 2]. This industry also employs intensified operations where the processing mixtures may show a complex phase behavior at different operating conditions including the presence of LLE [3]. Therefore, the knowledge and the capacity to describe the LLE behavior of multicomponent systems are very important for an adequate design and operation of food technology and purification facilities [1-3]. Herein, it is important to remark that LLE predictions are more difficult than those involved in vapor-liquid equilibrium (VLE) [4, 5]. However, the LLE data are essential for understanding the thermodynamic properties of multicomponent mixtures.
Various activity coefficient equations such as universal quasi chemical (UNIQUAC) [6] and non-random two liquid (NRTL) [7] can be used to model and predict the LLE data of mixtures involved in the food industry. These local composition models are effective and offer several advantages in terms of an easy numerical implementation without compromising the thermodynamic modeling performance; they can provide both accurate correlations and qualitatively correct predictions for design purposes. Overall, activity coefficient models require proper binary interaction parameters that can represent LLE data for highly non-ideal liquid mixtures usually encountered in food products extraction [8]. Herein, it is convenient to remark that the reliability of a thermodynamic model for predicting and correlating phase equilibrium data depends strongly on the value of its adjustable parameters. The parameters of thermodynamic models are usually estimated from the known experimental data via optimization procedures. Thisparameter identification stage can be considered as a challenging global optimization problem due to the nonlinearity of local composition models, the non-ideal thermodynamic behavior of liquid phases and the multicomponent nature of LLE systems. To address this type of parameter estimation problems, several optimization techniques have been reported in literature [3, 4, 8-20], which can be used for the processing of phase equilibrium data. However, current optimization methods may show drawbacks and failures in solving parameter estimation problems for multicomponent systems with LLE [9]. For example, Genetic Algorithms and Harmony Search may show drawbacks for finding the optimum parameters of local composition models for LLE modeling of biofuels [9]. Therefore, the search of better methods for performing, robustly and effectively, the parameter identification in LLE modeling is relevant for the process system engineering of the food industry.
The aim of this work was to introduce an alternative optimization framework, which is based on the Flower Pollination Algorithm (FPA), for the parameter identification in thermodynamic models applied to the processing of experimental LLE data in multicomponent systems. The Flower Pollination Algorithm [21] is a novel nature-inspired optimizer that is based on the characteristics of flowering plants. This metaheuristic has shown promising characteristics for global optimization in practical problems from engineering applications and it could be a suitable optimizer for performing thermodynamic calculations. However, to the best of authors’ knowledge, the application of Flower Pollination Algorithm for solving phase equilibrium problems has not yet been reported in the literature. Therefore, this study introduces the application ofthe Flower Pollination Algorithm (FPA) and its modified version (MFPA) for the parameter identification of the NRTL and UNIQUAC models internary and quaternary systems relevant for the food industry.
In the first part of this study, in order to analyze the performance of the Flower Pollination Algorithms, several LLE parameter estimation problems were solved using both local composition models and closure equations. In this stage, results showed that the predictions of UNIQUAC with closure equations offered the best performance for LLE prediction of tested ternary and quaternary systems. After that, the performanceof these stochastic methodswas compared,in terms of solution quality and computational efficiency, with previously applied metaheuristics such as Genetic Algorithm (GA), Simulated Annealing (SA), Harmony Search Algorithm (HAS) and Backtracking Search Optimization Algorithm (BSOA).In summary, our results show that Flower Pollination Algorithms may offer a better performance to solve the LLE parameter identification problem using multicomponent mixtures involved in the food industrial sector.
2. PARAMETER IDENTIFICATION FOR LIQUID-LIQUID EQUILIBRIUM MODELING
2.1. Description of Activity Coefficient Thermodynamic Models
The parameter identification in non-linear thermodynamic models used for LLE prediction and calculation has been of great interest in the literature [8-11]. Overall, the parameter identification involves the determination of model parameters, which should represent satisfactorily certain properties or characteristics of the system under study. The parameter identification problem in phase equilibrium modeling deals with equations that are non-linear-in-the-parameters and, consequently, robust optimization techniques have to be applied in its resolution [1, 9]. In particular, local composition models are traditionally used as the thermodynamic framework for the prediction and estimation of physicochemical properties of food systems involving liquid phases. These models are flexible and attractive for correlating and calculating the thermodynamic properties of a variety of compounds that includepolar, non-polar and associating systems. NRTL (Non-Random Two-Liquid) [7] and UNIQUAC (Universal Quasi- Chemical) [6] are models widely used for calculating the activity coefficients in food products systems. For the case of a multicomponent system, the NRTL model [7] is given by
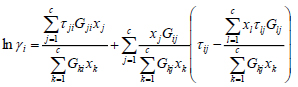 |
(1) |
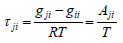 |
(2) |
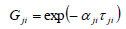 |
(3) |
where c is the number of components in the mixture, αji>= αij>, T is given in Kelvin and xj> is the mole fraction of component j, respectively. The corresponding equations for the UNIQUAC model [6] are given below
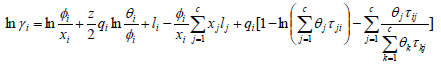 |
(4) |
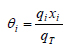 |
(5) |
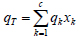 |
(6) |
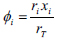 |
(7) |
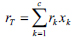 |
(8) |
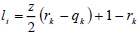 |
(9) |
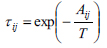 |
(10) |
where z = 10 and is the coordination number. These thermodynamic models have specific binary interactions parameters Aij for each component pair i and j of the multicomponent system. These parameters, in some way, characterize the energy of interaction between molecules i and j. Therefore, the identification of these parameters is necessary for thermodynamic calculations in theprocess system engineering involving liquid phases. The optimization procedure used in this study for solving the parameter identification problem in NRTL and UNIQUAC models is reported in the following section.
2.2. Optimization Problem for the Parameter Identification in NRTL and UNIQUAC Models
In this study, the LLE experimental data of several food products systems were used to determine the NRTL and UNIQUAC parameters using Flower Pollination Algorithms. Note that the parameter identification in local composition models is usually performed using LLE experimental data via the minimization of a suitable objective function. Herein, it is important to remark that the selection of the objective function used for the parameter identification influences both correlation and prediction results of thermodynamic models. According to literature [8-11], the objective function based on the isoactivity criterion for LLE suffers from the disadvantage that there is no a guarantee for representing accurately the experimental phase equilibrium compositions. Therefore, objective functions defined in terms of LLE concentrations (i.e., experimental tie-lines) are more proper for parameter identification in thermodynamic models. Based on these facts, the next objective function has been used for LLE data modeling [9]
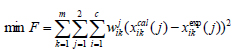 |
(11) |
where m is the number of experimental tie-lines used in the correlation procedure, xik(j) is the mole fraction of component i at liquid phase j at tie line k, wik is the weight associated with component i in phase j at tie line k, while cal and exp denote calculated and experimental values, respectively. This objective function, with unit weights wik, has been used for LLE modeling of food products systems. The calculation of the tie-lines using the activity coefficient models was performed with a flash calculation-based method [11].
In particular, Flower Pollination Algorithms have been employed for the minimization of equation (11) using the interaction parameters Aij> as decision variables. However, these binary interaction parameters not only affect the results of LLE modeling, but also they have an impact on the optimization procedure (i.e., constrained or unconstrained) that is employed for the parameter identification. In this study, the performance of FPA and MFPA has been tested with and without the application of closure equations [22] including its effect on results of LLE parameter estimation using an unconstrained problem formulation. The closure equation describes a linear relationship between the binary interaction parameters of local composition models for multicomponent mixtures and it is given by
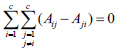 |
(12) |
Therefore, these closure equations can be written as follows for ternary systems [8, 9, 22, 23]
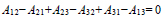 |
(13) |
Equation (13) indicates that only 5 out of 6 binary interaction parameters are independent and, consequently, the minimization of equation (11) can be performed selecting a set of 5 decision variables Aij and using equation (13) for determining the remaining one. There are 6 different sets of decision variables that can be employed for parameter identification in ternary systems using equation (13).
For the case of quaternary systems, the closure equations are
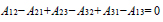 |
(14) |
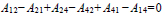 |
(15) |
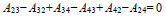 |
(16) |
In this case, only 9 out of 12 binary interaction parameters are independent and they can be used as decision variables for the unconstrained minimization of equation (12). For quaternary systems, there are 220 different sets of 9 decision variables Aij (i.e., 3 parameters being eliminated out of 12) for LLE parameter estimation and the other 3 parameters are obtained using equations (14) – (16). Herein, it is convenient to remark thatthere is no guideline for the selection of the independent Aij using closure equations and, consequently, this parameter selectioncan be performed arbitrarily. However, the results of parameter identification may vary depending on the selected set of Aij [9].
Finally, the goodness of the data fitting results between the observed and calculated mole fractions in food products systems was calculated in terms of the root mean square deviation (RMSD), which is defined as
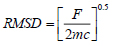 |
(17) |
These RMSD were calculated for both thermodynamic models and Flower Pollination Algorithms, which were used as performance metrics of algorithm reliability. As stated, the tie lines are evaluated by a LLE separation calculation using Newton method.
2.3. Description of Flower Pollination Algorithms
The Flower Pollination Algorithm (FPA) is a new metaheuristic inspired by the biological process of flower pollination. This algorithm was founded by Yang [21] in the year 2012. It was developed by the idea of flower pollination process. Flower pollination is the transport of pollen from a male flower to a female bloom. Pollination may take place in the form of biotic or abiotic. Pollinators such as birds, insects, bats, or other living beings help in the biotic pollination process. On the other hand, the abiotic pollination is related to transfer of pollen through wind and diffusion where no pollinator is required [24]. Based on these facts, the four rules employed to mimic the pollination characteristics of flowers [21, 25] are:
- Biotic and cross-pollination is considered as global pollination process with pollen-carrying pollinators performing Lévy flights.
- Abiotic and self-pollination are considered as local pollination.
- Flower constancy can be considered as the reproduction probability and it is proportional to the similarity of two flowers involved.
-
The interaction or switching of local pollination and global pollination can becontrolled by a switch probability p
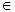 [0, 1] with a slight bias toward local pollination .
[0, 1] with a slight bias toward local pollination .
Then, the main steps of FPA, or simply the flower algorithm [21], are illustrated below:

On the other hand, the random selection of exploration and exploitation phases, which are based on the selected value of switching probability, sometimes causes the FPA to lose direction and move away from the global best solution.In this paper, an approach is introduced to enhance the performance of FPA specifically for LLE parameter estimation problems. A modification has been applied where i) the local pollination phase is modified by employing a scaling factor F to control the mutation occurring in flowers during pollination and ii) an additional intensive exploitation phase is added to improve the best solution. The details of the Modified Flower Pollination Algorithm (MFPA) are givenin [24]. Therefore, the pseudo-code of the MFPA can be summarized below:

Details of these algorithms are reported in [21, 24]. Both optimizers have been employed in the parameter identification of NRTL and UNIQUAC models using experimental data of thermodynamic systems related to the food industry. These algorithms were coded in MATLAB®2011a and were run on a Sony Vaio- Intel Core i3-3227U GHz- 4 GB RAM.
3. RESULTS AND DISCUSSION
3.1. Performance of FPA and MFPA for LLE Parameter Identification
In this first section, several examples are analyzed for illustrating the use of FPA and MFPA in the calculation of the binary parameters of NRTL and UNIQUAC models. These systems included 14 ternary and 8 quaternary systems relevant for food industry.Selected examples are listed in Table 1 along with their references and temperatures and details of these mixtures can be found in [26-31]. On the other hand, the parameters of Flower Pollination Algorithms were taken from [21, 24] except the population size, which was defined as NP = 5D for both methods where D is the number of decision variables (i.e., Aij used in the model parameter identification). Preliminary calculations in selected problems showed that these algorithm parameters were proper for performing LLE parameter identification in food-based systems. In particular, these results showed that NP and the stopping condition (i.e., convergence criterion) are the most relevant algorithm parameters of FPA for solving LLE data modeling. Note that, for multicomponent system with c ≥ 5, the population size of FPA should be increased to obtain a good numerical performance.
Food products systems used for parameter identification in liquid-liquid equilibrium modeling using Flower Pollination Algorithms.
| System No. | Ternary system: A1 + A2 + A3 | T, K | Reference |
|---|---|---|---|
| 1 | Water + levulinic acid + dimethyl succinate | 298.15 | [26] |
| 2 | Water + levulinic acid + glutarate | 298.15 | [26] |
| 3 | Water + levulinic acid + dimethyl adipate | 298.15 | [26] |
| 4 | Water + levunilic acid + isoamyl alcohol | 298.15 | [27] |
| 5 | Water + levunilic acid + hexanol | 298.15 | [27] |
| 6 | Water + levunilic acid + decanol | 298.15 | [27] |
| 7 | Water + 1-butanol + β-pinene | 298.15 | [28] |
| 8 | Water + 1-butanol + α-pinene | 298.15 | [28] |
| 9 | Water + 1-butanol + limonene | 298.15 | [28] |
| 10 | Water + butyric acid + diethyl adipate | 298.2 | [29] |
| 11 | Water + butyric acid + diethyl glutarate | 298.2 | [29] |
| 12 | Water + butyric acid + diethyl succinate | 298.2 | [29] |
| 13 | palm oil + oleic acid + anhydrous ethanol | 318.2 | [30] |
| 14 | palm oil + palmitic acid + anhydrous ethanol | 318.2 | [30] |
| No. | Quaternary system: A1 + A2 + (A3+ A4) | T, K | Reference |
| 1 | Palm oil + palmitic acid + (ethanol 93.9% + water 6.10%) | 318.2 | [30] |
| 2 | Palm oil + palmitic acid + (ethanol 87.59% + water 12.41%) | 318.2 | [30] |
| 3 | Palm oil + oleic acid + (ethanol 93.9% + water 6.10%) | 318.2 | [30] |
| 4 | Palm oil + oleic acid + (ethanol 87.59% + water 12.41%) | 318.2 | [30] |
| 5 | Limonene + carvone + (ethanol 89.02% + water 10.98%) | 298.2 | [31] |
| 6 | Limonene + carvone + (ethanol 76.36% + water 23.64%) | 298.2 | [31] |
| 7 | Limonene + carvone + (ethanol 70.96% + water 29.04%) | 298.2 | [31] |
| 8 | Limonene + carvone + (ethanol 68.67% + water 31.33%) | 298.2 | [31] |
All LLE parameter identification problems were solved 50 times with random number seeds and different initial values. Parameter identification was performed using the next bounds for Aij
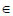 (-1000, 2000). According to literature [7], the non-randomness parameter αij of NRTL equationcan be set to a predetermined value ranging from 0.2 to 0.5 for LLE calculations. In this study, this NRTL parameter was defined as 0.3, while the volume r and the surface area q parameters of UNIQUAC model for each component were taken from [28, 30, 31] and Aspen HYSYS Software.
(-1000, 2000). According to literature [7], the non-randomness parameter αij of NRTL equationcan be set to a predetermined value ranging from 0.2 to 0.5 for LLE calculations. In this study, this NRTL parameter was defined as 0.3, while the volume r and the surface area q parameters of UNIQUAC model for each component were taken from [28, 30, 31] and Aspen HYSYS Software.
The performances of FPA and MFPA were quantified and compared based on two metrics: the RMSD values for both thermodynamic models after the minimization of equation (11) and the number of objective function evaluations (NFE) involved in the parameter identification. Four systems were selected as benchmarking examples to illustrate the numerical performance of FPA and MFPA in the parameter estimation for LLE modeling. These mixtures correspond to the predictions of LLE for the ternary and quaternary mixtures: a) water + levulinic acid + dimethyl succinateat 298.15K, b) water + levulinic acid + glutarateat 298.15K, c) palm oil + palmitic acid + ethanol + water at 318.2 K and d) limonene + carvone + ethanol + water at 298.2 K. The parameter identification for these LLE mixtures has been solved using FPA and MFPA with four different operating scenarios. These scenarios corresponded to the use of both FPA and MFPA with and without the application of closure equations and local optimization. This approach has been used in a previous study [9] and it has been applied in this article for comparison purposes with other metaheuristics. The nomenclature used for results reported in this section is: FPA-C and MFPA-C for flower pollination algorithms with closure equations; FPA-CL and MPFA-CL for flower pollination algorithms with both closure equation and local optimization, respectively. The function fmincon of MATLAB® was employed as local optimization in these calculations.
The convergence profiles of FPA and MFPA,with and without closure equations,during the parameter identification of NRTL and UNIQUAC models forwater + levulinic acid + dimethyl succinate at 298.15 and palm oil + palmitic acid + ethanol + water at 318.2 K are reported in Fig. (1). Overall, the convergence performance of both FPA and MFPA is typical of population-based methods where a step-function is observed. As expected, the value of objective function improves with the numerical effort (i.e., number of generations or function evaluations). However, the application of closure equation for parameter identification of NRTL and UNIQUAC models improves significantly the convergence rate of both FPA and MFPA. In particular, MFPA converged faster and reached the lowest values for the objective function in tested examples with both thermodynamic models, see Fig. (2).
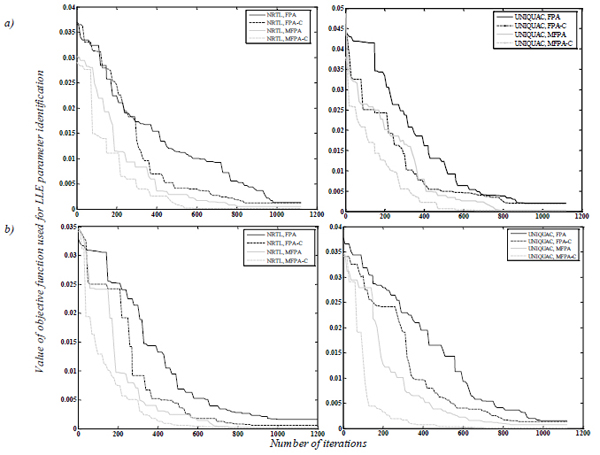
Convergence performance of Flower Pollination Algorithms, with and without closure equations, for LLE parameter identification using NRTL and UNIQUAC models in food products systems. Mixtures: a) water + levulinic acid + dimethyl succinate at 298.15 K and b) palm oil + palmitic acid + ethanol + water at 318.2 K.
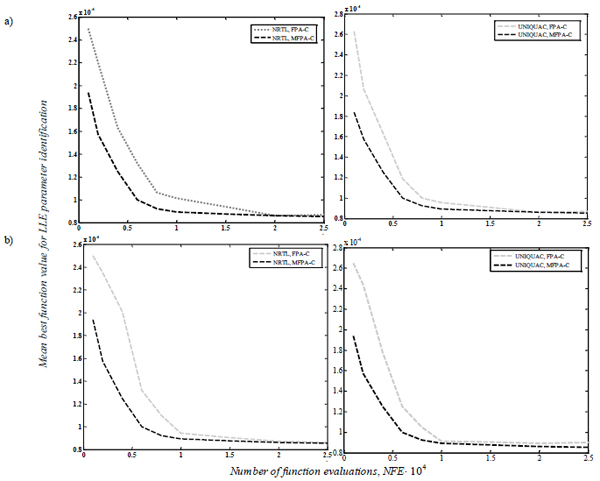
Evolution of the mean best function value versus NFE for Flower Pollination Algorithms with closure equations for LLE parameter identification of NRTL and UNIQUAC models in food products systems. Mixtures: a) water + levulinic acid + dimethyl succinate at 298.15 K and b) palm oil + palmitic acid + ethanol + water at 318.2 K.
Particularly, MFPA with closure equation is effective for finding the interaction parameters Aij of the NRTL and UNIQUAC models. Note that the application of a scaling factor to control the mutation in the local pollination phase and the additional intensive exploitation phase appear to aid the exploration capabilities for global optimization of MFPA. In terms of the efficacy, MFPA showed the best performance especially at low values of NFE and this numerical trend prevails for both NRTL and UNIQUAC models. Overall, results showed that 600th iterations of MFPA-C are sufficient to find the optimal parametersin these LLE problems, while FPA with and without closure equations required more than 800 iterations for reaching convergence. In both cases, further generations only seem to improve marginally the solution obtained independently of the application of closure equation. However, the use of closure equation for LLE parameter identification helps to reduce significantly the numerical effort during the model parameter identificationwith these stochastic solvers. In particular, the impact of using closure equation on algorithm efficacy and convergence rate is more evident at early stages of parameter identification, see Figs. (1) and (2). This relevant numerical performance has also reportedfor the LLE modeling of other thermodynamic systems using nature-inspired optimizers [9].
RMSD values obtained by FPA and MFPA for the benchmark ternary and quaternary mixtures are given in Fig. (3). It is clear that MFPA with closure equation can achieve lower RMSD values than those obtained for FPA in this set of ternary and quaternary systems. Furthermore, the application of the local optimization methodimproves the precision of solution obtained for LLE parameter estimation using FPA and MFPA. On the other hand, UNIQUAC model offered a better correlation performance than NRTL model for LLE data of selected ternary and quaternary systems. RMSD values ranged from 0.002 to 0.01 for UNIQUAC model using FPA and MFPA, see Fig. (3).
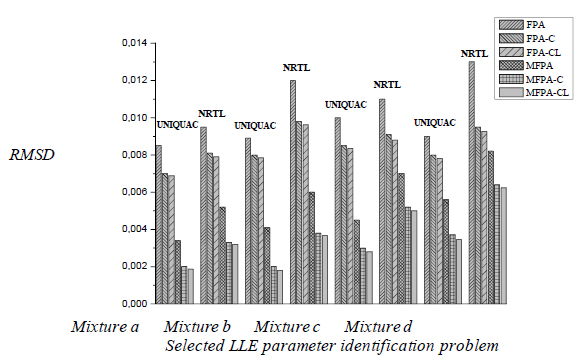
RMSD values of Flower Pollination Algorithms for LLE parameter identification of NRTL and UNIQUAC models in food products systems. Mixtures: a) water + levulinic acid + dimethyl succinate at 298.15K, b) water + levulinic acid + glutarate at 298.15 K, c) palm oil + palmitic acid+ ethanol + water at 318.2 K and d) limonene + carvone + ethanol + water at 298.2 K.
As stated, the closure equation was used to reduce the number of interaction parameters (Aij) to be determined during the global minimization of equation (11). However, there are different possibilities for defining the five or the nine decision variables used during LLE data fitting of ternary and quaternary food products systems using this closure equation. For illustration, the results of LLE data modeling for the different possibilities of Aij parameter elimination are reported in Table 2 for selected food products mixtures using both NRTL and UNIQUAC equations. It is clear that the RMSD values obtained with both FPA and MFPA depend on the set of interaction parameters selected. Similar findings have been reported by [8, 9] for the modeling of LLE data using stochastic optimizers. The selection of different Aij may modify the search space affecting the optimization trajectories selected by the numerical method and, consequently, it mayimpact the performance of stochastic optimizers [9]. Therefore, the best option for parameter elimination using closure equations should be identified to improve the results of LLE data modeling. However, it is interesting to remark that MFPA outperformed FPA, in terms of RMSD values, independent of Aij selected as decision variables for parameter identification. This trend prevails for both NRTL and UNIQUAC models.
Results of LLE parameter identification in selected ternary and quaternary systems using FPA and MFPA and closure equations with different parameter elimination.
| RMSD for NRTL model | RMSD for UNIQUAC model | ||||
|---|---|---|---|---|---|
| Thermodynamic system | Parameter Elimination | FPA-C | MFPA-C | FPA-C | MFPA-C |
| water + levulinic acid + dimethyl succinate | A12 | 0.0087 | 0.0021 | 0.0065 | 0.0018 |
| A21 | 0.0098 | 0.0013 | 0.0072 | 0.0028 | |
| A13 | 0.0086 | 0.0035 | 0.0068 | 0.0016 | |
| A31 | 0.0094 | 0.0018 | 0.0078 | 0.0011 | |
| A23 | 0.0092 | 0.0017 | 0.0069 | 0.0026 | |
| A32 | 0.0084 | 0.0023 | 0.0085 | 0.0036 | |
| water + levulinicacid + glutarate | A12 | 0.0092 | 0.0018 | 0.0070 | 0.0025 |
| A21 | 0.0082 | 0.0021 | 0.0052 | 0.0013 | |
| A13 | 0.0078 | 0.0040 | 0.0061 | 0.0013 | |
| A31 | 0.0075 | 0.0032 | 0.0054 | 0.0018 | |
| A23 | 0.0073 | 0.0015 | 0.0047 | 0.0026 | |
| A32 | 0.0083 | 0.0020 | 0.0045 | 0.0035 | |
| palm oil + palmitic acid + (ethanol 93.9% + water 6.10%) | 3 parameters Aij | 0.0092a | 0.0078b | 0.0088c | 0.0032d |
| limonene + carvone + (ethanol 76.36% + water 23.64%) | 3 parameters Aij | 0.0072e | 0.0037f | 0.0081g | 0.0041h |
The results of FPA and MFPA for solving the LLE parameter identification problems along with the corresponding best values of RMSD for all the food products systems are reported in Tables 3-6. These results correspond to the application of both algorithms with and without the closure equations. Results confirmed that MFPA-C provides the best values of RMSD for all ternary and quaternary systems. Overall, the UNIQUAC model was able to accurately describe the experimental LLE compositions and showed better data fitting results than those obtained with NRTL model. For illustration, the phase diagrams of selected food products systems using the best interaction parameters of UNIQUAC model are reported in Fig. (4). The comparison of tie-line compositions indicated that the experimental and calculated LLE data agreed very well using this activity coefficient model.
Results of NRTL interaction parameters for LLE modeling of ternary systems relevant for food industry using Flower Pollination Algorithms.
| System No. | NRTL interaction parameters, K | Best value of RMSD | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| A12 | A21 | A13 | A31 | A23 | A32 | FPA | FPA-C | MFPA | MFPA-C | |
| 1 | 70.58 | 65.82 | 1307.06 | 561.48 | 325.47 | -415.35 | 0.0092 | 0.0082 | 0.0059 | 0.0016 |
| 2 | 73.18 | 49.80 | 539.58 | 843.77 | 407.66 | 735.23 | 0.0086 | 0.0071 | 0.0058 | 0.0013 |
| 3 | 102.40 | 67.59 | 1122.87 | 603.88 | 856.11 | 371.93 | 0.0100 | 0.0090 | 0.0086 | 0.0048 |
| 4 | 114.40 | 76.38 | 1051.97 | 388.06 | 1205.35 | 579.46 | 0.0093 | 0.0073 | 0.0059 | 0.0035 |
| 5 | 93.21 | 88.25 | 873.92 | 284.65 | 907.63 | 323.32 | 0.0096 | 0.0080 | 0.0067 | 0.0015 |
| 6 | 158.68 | 283.51 | 1122.89 | 997.03 | 792.38 | 541.69 | 0.0121 | 0.0093 | 0.0091 | 0.0063 |
| 7 | 372.29 | -183.72 | 1280.17 | 479.83 | 1053.45 | 809.12 | 0.0113 | 0.0095 | 0.0080 | 0.0047 |
| 8 | 382.21 | -122.61 | 1197.56 | 511.38 | 1008.41 | 827.05 | 0.0088 | 0.0072 | 0.0064 | 0.0045 |
| 9 | 528.27 | -155.32 | 1231.13 | 408.16 | 1120.92 | 981.54 | 0.0097 | 0.0083 | 0.0076 | 0.0048 |
| 10 | -247.37 | -339.83 | 997.60 | 513.48 | 1266.58 | 874.92 | 0.0075 | 0.0051 | 0.0048 | 0.0030 |
| 11 | -122.85 | -507.18 | 1305.28 | 492.61 | 1100.42 | 672.08 | 0.0079 | 0.0059 | 0.0069 | 0.0022 |
| 12 | -318.21 | -282.95 | 1191.62 | 686.73 | 1295.48 | 755.33 | 0.0091 | 0.0069 | 0.0077 | 0.0050 |
| 13 | 687.83 | 450.72 | 958.17 | 465.09 | 1184.57 | 928.60 | 0.0110 | 0.0090 | 0.0085 | 0.0067 |
| 14 | 1033.56 | 718.23 | 1262.93 | 385.87 | 987.61 | 425.88 | 0.0098 | 0.0079 | 0.0058 | 0.0031 |
Results of UNIQUAC interaction parameters for LLE modeling of ternary systems relevant for food industry using Flower Pollination Algorithms.
| System No. | UNIQUAC interaction parameters, K | Best value of RMSD | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| A12 | A21 | A13 | A31 | A23 | A32 | FPA | FPA-C | MFPA | MFPA-C | |
| 1 | -283.10 | 425.39 | 1120.72 | 886.15 | 1368.91 | 425.85 | 0.0088 | 0.0066 | 0.0066 | 0.0010 |
| 2 | -83.51 | 261.10 | 1034.05 | 628.37 | 1286.47 | 536.18 | 0.0082 | 0.0048 | 0.0052 | 0.0015 |
| 3 | 197.82 | 381.21 | 1126.94 | 465.14 | 1371.37 | 526.18 | 0.0110 | 0.0086 | 0.0082 | 0.0044 |
| 4 | 319.45 | 238.67 | 1053. 23 | 548.18 | 1203.98 | 779.71 | 0.0093 | 0.0058 | 0.0058 | 0.0030 |
| 5 | -98.27 | 416.71 | 1007.88 | 892.31 | 1317.02 | 686.47 | 0.0086 | 0.0046 | 0.0064 | 0.0018 |
| 6 | 451.11 | 763.36 | 1279.77 | 1055.48 | 1362.15 | 825.61 | 0.0154 | 0.0098 | 0.0083 | 0.0058 |
| 7 | 518.72 | -397.85 | 927.16 | -243.32 | 1180.33 | 926.42 | 0.0103 | 0.0087 | 0.0071 | 0.0042 |
| 8 | 959.72 | 183.65 | 1042.63 | -311.82 | 1295.44 | 717.06 | 0.0087 | 0.0040 | 0.0061 | 0.0038 |
| 9 | 1153.45 | 621.92 | 946.27 | -418.62 | 1316.73 | 483.37 | 0.0089 | 0.0052 | 0.0069 | 0.0041 |
| 10 | 753.48 | -285.26 | 829.54 | -575.83 | 1082.65 | 716.02 | 0.0073 | 0.0038 | 0.0050 | 0.0021 |
| 11 | 910.12 | -435.78 | 1295.49 | -821.58 | 1312.65 | 541.48 | 0.0077 | 0.0041 | 0.0067 | 0.0013 |
| 12 | 1125.47 | 276.13 | 1050.35 | -387.56 | 1379.62 | 791.05 | 0.0082 | 0.0057 | 0.0073 | 0.0015 |
| 13 | -273.21 | 432.13 | 812.44 | 589.97 | 1281.89 | 354.08 | 0.0097 | 0.0073 | 0.0081 | 0.0048 |
| 14 | 186.73 | 709.24 | 1104.58 | 967.81 | 1308.62 | 649.34 | 0.0089 | 0.0066 | 0.0078 | 0.0055 |
Results of NRTL interaction parameters for LLE modeling of quaternary systemsrelevant for food industry using Flower Pollination Algorithms.
| System No. | NRTL interaction parameters, K | Best value of RMSD | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| A12, A21 | A13, A31 | A14, A41 | A23, A32 | A24, A42 | A34, A43 | FPA | FPA-C | MFPA | MFPA-C | |
| 1 | 688.87, 733.01 | 460.79, 937.14 | 1547.98, 1509.81 | 684.79, 1117.00 | 837.17, 754.86 | 1216.73,702.21 | 0.0096 | 0.0062 | 0.0065 | 0.0042 |
| 2 | 674.73 , 718.90 | 446.69, 923.11 | 1533.82, 1495.65 | 670.62, 1102.87 | 823.10, 740.76 | 1202.78, 688.19 | 0.0095 | 0.0080 | 0.0048 | 0.0036 |
| 3 | 645.17 , 538.87 | 176.11 , 474.62 | 1347.80 , 1224.61 | 453.09 , 857.90 | 643.28 , 626.39 | 726.92 , 305.22 | 0.0120 | 0.0096 | 0.0050 | 0.0022 |
| 4 | 787.78, 681.50 | 318,63, 617.23 | 1490,38,1367.21 | 595,61, 1000.51 | 785,89, 769.00 | 869, 53, 447.74 | 0.0098 | 0.0086 | 0.0076 | 0.0065 |
| 5 | 1266.14, 619.5 | 1032.48, 266.24 | 728.35, 543.58 | 1357.07,1237.47 | 613.69,1075.56 | -49.80, 531.67 | 0.0132 | 0.0098 | 0.0080 | 0.0068 |
| 6 | 1206.14, 632.03 | 1020.74, 283.98 | 685.68, 598.81 | 1381.57, 1218.92 | 605.52, 1092.76 | -81.00, 568.89 | 0.0098 | 0.0088 | 0.0078 | 0.0060 |
| 7 | 1270.29, 656.33 | 1030.93, 262.32 | 698.52, 570.63 | 1379.42, 1224.77 | 610.22, 1096.29 | -72.24, 568.48 | 0.0200 | 0.0110 | 0.0082 | 0.0071 |
| 8 | 1261.52, 624.18 | 1046.79, 285.86 | 708.83, 550.58 | 1352.33, 1228.74 | 611.08, 1090.17 | -58.82, 543.86 | 0.0180 | 0.0105 | 0.0089 | 0.0052 |
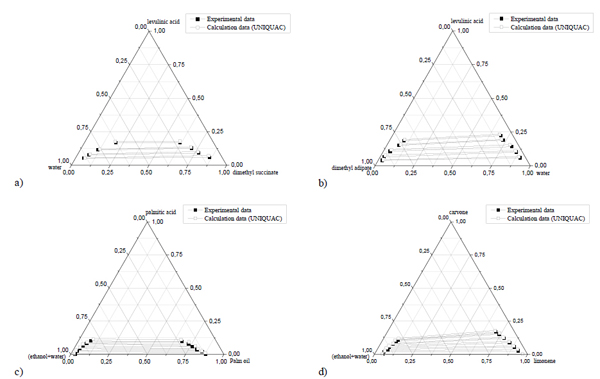
Experimental and adjusted data LLE of a) water + levulinic acid + dimethyl succinate at 298.15 K, b) water + levulinic acid + glutarate at 298.15 K, c) palm oil + palmitic acid + ethanol + water at 318.2 K and d) limonene + carvone + ethanol + water at 298.2 K using MFPA with closure equations.
Results of UNIQUAC interaction parameters for LLE modeling of quaternary systemsrelevant for food industry using Flower Pollination Algorithms.
| System No. | UNIQUAC interaction parameters, K | Best value of RMSD | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| A12, A21 | A13, A31 | A14, A41 | A23, A32 | A24, A42 | A34, A43 | FPA | FPA-C | MFPA | MFPA-C | |
| 1 | 288.23, -518.37 | 201.06, -212.16 | 1245.09, 462.18 | -217.46, 175.92 | 772.83, 796.52 | 243.46, -126.23 | 0.0086 | 0.0062 | 0.0052 | 0.0026 |
| 2 | 261.82, -507.93 | 185.18, -199.42 | 1228.23, 481.79 | -215.04, 170.11 | 769.43, 792.74 | 239.26, -122.58 | 0.0092 | 0.0076 | 0.0045 | 0.0020 |
| 3 | 345.73, -450.61 | 213.11, -164.06 | 1173.42, 439.84 | -200.92, 218.25 | 658.91, 721.67 | 228.63, -127.78 | 0.010 | 0.0091 | 0.0042 | 0.0010 |
| 4 | 678.70, 1310.60 | 713.32, -252.96 | 373.48, 675.68 | 1302.70,-295.48 | 1426.90,1097.20 | -782.92, 485.56 | 0.0120 | 0.0096 | 0.0073 | 0.0035 |
| 5 | 376.23, 1137.81 | 1092.57, 996.73 | 1242.03,1298.31 | 434.63, -422.79 | 1019.76, 314.46 | 873.32, 1025.44 | 0.0098 | 0.0078 | 0.0065 | 0.0028 |
| 6 | 372.56, 1102.37 | 1115.97, 990.58 | 1260.18, 1285.77 | 429.18, -426.02 | 1015.21, 310.99 | 871.07, 1022.05 | 0.0095 | 0.0072 | 0.0080 | 0.0042 |
| 7 | 385.22, 1098.75 | 1146.18,1002.26 | 1265.85, 1281.16 | 431.52, -425.93 | 1011.87, 313.65 | 867.48, 1026.71 | 0.0160 | 0.0098 | 0.0077 | 0.0052 |
| 8 | 387.61, 1092.83 | 1149.28,1006.44 | 1268.36, 1275.94 | 425.74, -422.32 | 1009.52, 311.88 | 786.12, 1026.54 | 0.0120 | 0.0095 | 0.0066 | 0.0043 |
3.2. Performance Comparison of Flower Pollination Algorithmsand Other Nature-Inspired Stochastic Methods applied in LLE Parameter Identification
The numerical performance of FPA and MFPA has been compared with the efficacy of other metaheuristics algorithms, with and without closure equations and local optimization, for performing the LLE parameter identification in tested food products systems. For this analysis, the ternary and quaternary systems reported in Table 2 have been employed. The methods assed in this stage were: Genetic Algorithm (GA), Simulated Annealing (SA), Harmony Search Algorithm (HSA) and Backtracking Search OptimizationAlgorithm (BSOA). Results of this comparative study are reported in Figs. (5) and (6).

RMSD values of FPA, MFPA, SA, GA, HAS and BSOA (with and without closure equations and local optimization) for LLE parameter identification using NRTL and UNIQUAC models in selected food products systems. Mixtures: a) water + levulinic acid + dimethyl succinate at 298.15 K, b) water + levulinic acid + glutarate at 298.15 K, c) palm oil + palmitic acid+ ethanol + water at 318.2 K and d) limonene + carvone + ethanol + water at 298.2 K.
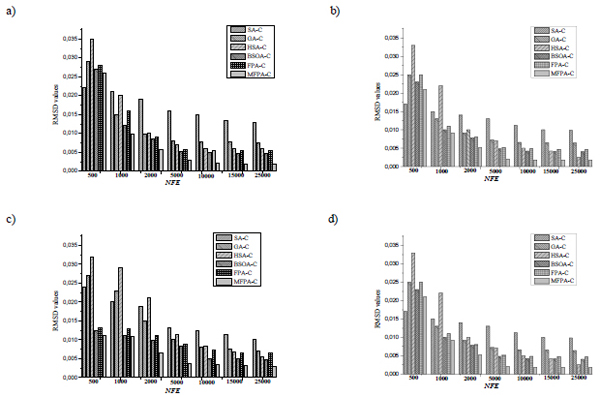
RMSD versus NFE for FPA, MFPA, SA, GA, HAS and BSOA with closure equations for LLE parameter identification using NRTL and UNIQUAC models in selected food products systems. Mixtures: a) water + levulinic acid + dimethyl succinate at 298.15 K, b) water + levulinic acid + glutarate at 298.15 K, c) palm oil + palmitic acid + ethanol + water at 318.2 K and d) limonene + carvone + ethanol + water at 298.2 K.
In particular, Fig. (5) shows the RMSD values obtained during the parameter estimation of NRTL and UNIQUAC models for the selected food products systems using all stochastic solvers. It is clear that MFPA outperformed all other algorithms in terms of reliability (i.e., it showed the lowest values of RMSD) with and without the closure equations and local optimization. It is interesting to remark that the use of the local optimization has more impact on the performance ofthe other stochastic methods in comparison to Flower Pollination Algorithms. This result suggests that FPA and MFPA may show better exploration capabilities for finding the optimum parameters Aij.
On the other hand, Fig. (6) shows the evolution of the RMSD values versus NFE for all optimizers used for LLE parameter estimation of local composition models in selected ternary and quaternary systems. Overall, the most reliable algorithms for LLE modeling are BSOA, FPA and MFPA, which outperformed GA, SA and HAS. In particular, MFPA may reach a high precision in the solution obtained for LLE parameter identification. It is clear that the application of closure equation improves the solution quality of the stochastic methods irrespective of the used model. For all mixtures, the MFPA with closure equations offered the best tradeoff between reliability and numerical effort for both NRTL and UNIQUAC models.
CONCLUSION
This paper introduces the application of Flower Pollination Algorithms to phase equilibrium calculations of LLE systems. In particular, this novel metaheuristic has been applied in the parameter identification of UNIQUAC and NRTL models from ternary and quaternary systems relevant for food products mixtures. In general, Modified Flower Pollination Algorithm performed better than the original Flower Pollination Algorithm in LLE parameter identification with and without the application of closure equations. In fact, Modified Flower Pollination Algorithm with closure equations showed better solution quality and convergence characteristics for all the multicomponent systems tested in this study. This novel stochastic method outperformed other metaheuristics such as Genetic Algorithm, Harmony Search or Simulated Annealing in LLE parameter identification. However, the parameter identification involving closure equations may impact on results of LLE modeling if a proper selection of the independent parameters Aij is not performed. On the other hand, UNIQUAC model offers a better performance than NRTL model for LLE modeling in testedfood product mixtures. Therefore, this local composition model is a proper choice for thermodynamic calculations involved in the process system engineering of food-based multicomponent mixtures.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
Authors acknowledge the financial support provided by University of Biskra and Instituto Tecnologico de Aguascalientes.


