RESEARCH ARTICLE


Kinetics of Decomposition Reactions of Acetic Acid Using DFT Approach



Anand Mohan Verma, Nanda Kishore*
Department of Chemical Engineering, Indian Institute of Technology Guwahati, Assam, India – 781039

Article Information


Identifiers and Pagination:

Year: 2018
Volume: 12
First Page: 14
Last Page: 23
Publisher ID: TOCENGJ-12-14
DOI: 10.2174/1874123101812010014

Article History:

Received Date: 17/08/2017
Revision Received Date: 01/12/2017
Acceptance Date: 21/01/2018
Electronic publication date: 08/02/2018
Collection year: 2018

Article Metrics

CrossRef Citations:
8
Total Statistics:

Full-Text HTML Views: 6120
Abstract HTML Views: 2247
PDF Downloads: 1533
ePub Downloads: 956
Total Views/Downloads: 10856
Unique Statistics:

Full-Text HTML Views: 3201
Abstract HTML Views: 1239
PDF Downloads: 900
ePub Downloads: 511
Total Views/Downloads: 5851



Creative Commons License
© 2018 Verma and Kishore.

open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: https://creativecommons.org/licenses/by/4.0/legalcode. This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

* Address correspondence to this author at the Department of Chemical Engineering, Indian Institute of Technology Guwahati, Assam, India – 781039; Tel: +91-361-258-2276; E-mails: nkishore@iitg.ernet.in; mail2nkishore@gmail.com


Abstract

Object:

Excessive amount of oxygen content in unprocessed bio-oil deteriorates the quality of bio-oil which cannot be used in transportation vehicles without upgrading. Acetic acid (CH3COOH) is a vital component of ‘acids’ catalogue of unprocessed bio-oil produced from thermochemical conversions of most of biomass feedstocks such as switchgrass, alfalfa, etc. In this study, the decomposition reactions of acetic acid are carried out by two reaction pathways, i.e., decarboxylation and dehydration reactions. In addition, the reaction rates of decomposition are analysed in a wide range of temperatures, i.e., 298-900 K and at atmospheric pressure.

Method:

All quantum chemical calculations are performed in the gas phase using two DFT functionals, B3LYP and M06-2X, with 6-31g(d) basis set. The dehydration reaction of acetic acid proceeds directly from ground state structure of acetic acid, whereas, decarboxylation reaction forms an unstable intermediate of acetic acid to initiate the proton migration. Barrier height and kinetics study for both reactions and theories are different and illustrated in the reaction pathway and rate profiles, respectively. Furthermore, both levels of theories offer similar structural configurations but they differ slightly in energetics.

Conclusion:

The reaction kinetics of both reactions is linearly fitted and the Arrhenius equations corresponding to each decomposition mechanism are generated by fitting the data from line equation.

Keywords: Acetic acid, Reaction pathway, Bio-oil, DFT, Decomposition reaction, Reaction. kinetics.

1. INTRODUCTION

Non-renewable energy resources, particularly, fossil fuels are depleting at an excessive rate and it could be in scarce for the next generation. To overcome this problem, most of the countries have started to use renewable energy sources to maintain the energy demands; and climate concerns caused by the fossil fuels. Biomass is one and the only promising renewable energy resource which can be exploited to acquire sustainable carbon for transportation vehicles and platform chemicals [1]. The bio-oil from thermochemical conversions of lignocellulosic biomass contains a vast amount of oxy-compounds, more than 300, which are classified into various oxy-catalogues, e.g., acids, alcohols, ethers, furans, phenolic, miscellaneous oxygenates, etc [2]. Acetic acid is a promising model compound of ‘acids’ catalogue of unprocessed bio-oil compounds produced from most of the biomass feedstocks. Mullen et al. [3] have reported weight percentages of acetic acid as 2.94 wt. %, 2.26 wt. %, and 3.49 wt. % in their bio-oil production experiments from switchgrass, alfalfa early bud, and alfalfa full flower, respectively. Since, bio-oil is a mixture of more than 300 oxygenated compounds, the weight percentage of ~3-4% is a huge quantity. This is one of the reasons why most of bio-

oil upgradation researches are based on acetic acid compound. These excessive amount of oxy-compounds cause various drawbacks in terms of low heating value, low pH, low stability, high viscosity, etc.; therefore, the bio-oil produced from thermochemical conversions of lignocellulosic biomass needs to be upgraded to reduce oxygen functionalities.

Out of various decomposition mechanisms of acetic acid, two favourable unimolecular decomposition reaction of acetic acid are decarboxylation reaction and dehydration reaction [4, 5]. Decarboxylation reaction of acetic acid yields methane and carbon di oxide molecules, whereas, dehydration reaction of acetic acid produces a simplest ketene group called ethenone molecule and water compound. The decomposition reactions of acetic acid are as follows:

(1) (2)

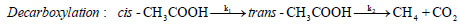
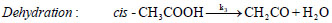
In decarboxylation reaction of acetic acid, the ground state structure of acetic acid (cis-CH3COOH) first undergoes dihedral change to produce a less stable acetic acid structure, i.e., trans-CH3COOH, which migrates hydrogen atom from –COOH group to methyl group to produce methane molecule and on the other hand, cleavage of C–C sigma bond occurs to form carbon dioxide compound. In dehydration reaction, methyl group of cis-CH3COOH donates its one of the hydrogen atom to OH of –COOH group to produce water and ethenone compounds [4-7]. The decomposition reactions of acetic acid have been studied by several researchers in past using experimental and computational means. For instance, Nguyen et al. [4] performed decomposition reaction of acetic acid at MP2/6-3lg(d,p) level of theory and reported barrier heights required by decarboxylation reaction and dehydration reactions as 71.89 kcal/mol and 74.28 kcal/mol, respectively. Pinho et al. [5] carried out numerical work on acetic acid to check the accuracy and reliability of the methods and found that MP2 and CASSCF/6-31g(d) level of theories do not deviate significantly with the experiments. Bamford et al. [6]. Performed an experiment to find out the kinetic parameters of the decomposition reaction of acetic acid for a temperature range of 770–920oC and reported expressions for the rate constants of both reactions (1) and (2) as:

(3)

Blake et al. [7, 8] also reported kinetic parameters of the decomposition reactions of acetic acid for a temperature range of 530-1950 K. They observed that decarboxylation reaction of acetic acid follows first order reaction kinetics for a wide temperature range of 530-1950 K, whereas, dehydration reaction of acetic acid follows second order reaction kinetics for temperature below 600 K and first order reaction kinetics above 600 K. Mackie et al. [9] performed kinetic analysis for the decomposition of acetic acid in dilute argon in a single pulse shock tube over a temperature range of 1300–1950 K. They reported that both reactions show first order reaction kinetics for a temperature range of 1300–1950 K; and activation energy ranges from 64.84 kcal/mol to 70.46 kcal/mol for reaction (1) and 67.45 kcal/mol to 70.46 kcal/mol for reaction (2). Duan et al. [10]. performed a numerical work for the decomposition reaction of acetic acid with both, decarboxylation reaction and dehydration reaction, routes in gas phase medium and they also compared decarboxylation reaction with water catalysed medium using MØller–Plesset second order perturbation (MP2) theory. They reported activation energy of 76 kcal/mol for dehydration reaction, whereas, for decarboxylation reaction, they reported activation energies of 77.31 kcal/mol and 64 kcal/mol for gas phase and water catalysed phase, respectively.

To the best of authors’ knowledge, kinetic analyses of decomposition reactions of acetic acid in temperature range of 298–900 K using density functional theory (DFT) are incomplete in literature. To fill this gap of information, we propose the kinetic study for the decomposition reaction of acetic acid using B3LYP and M06-2X functionals of DFT with the basis set of 6-31g(d) for a temperature range of 298–900 K at atmospheric pressure. In addition, the reaction kinetics of both reactions are linearly fitted and the Arrhenius equations corresponding to each decomposition mechanism are generated by fitting the data from line equation.

2. COMPUTATIONAL DETAILS

Minimum and transition state geometries are optimized by B3LYP (Becke-3 parameter-Lee-Yang-Parr) [11, 12] and M06-2X (Minnesota functional of 06 family) [13, 14] functionals of density functional theory (DFT) [15-17] with 6-31g(d) [18, 19] basis set. Transition state structures are identified as the first order saddle points by obtaining a single imaginary frequency in frequency results of normal mode vibrational frequency calculations. To affirm the transition state structure as the actual transition state which links to two minima through the minimum energy path, an IRC [20] calculation at the same level of theory as of optimization theory has been carried out. All quantum chemical calculations are performed in gas phase using Gaussian 09 [21] and Gauss View 5 [22] software packages. For kinetic analyses, thermochemical parameters are obtained from vibrational analyses for a wide range of temperature 300-900 K and fixed pressure of 1 atm. The evaluation of reaction rate constants are carried out by solving the Eyring’s transition state theory [23] which is:

(4)

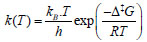
where kB is the Boltzmann's constant (1.30662 Х 10-23 JK-1); h is the Planck's constant (6.0626176 Х 10-34 J.sec); T is temperature in Kelvin; and R is universal gas constant (1.987 kcal mol-1). The free energy barrier, ∆‡G (kcal mol-1) is given as the formula below:

(5)

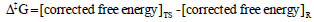
3. RESULT AND DISCUSSION

The ground state structure of acetic acid is found in cis conformer shown in structure R of Table 1. However, the decomposition of acetic acid by decarboxylation method undergoes through intermediate trans–CH3COOH which is an unstable acetic acid structure compared to cis conformer. On the other hand, dehydration reaction starts from cis–conformer of acetic acid. The vibrational frequency analyses for both decomposition reactions are carried out at 298, 300–900 K with an interval of 100 K, and the thermochemistry parameters, involving Gibbs free energy and enthalpy, are given in supplementary information.

Table 1. The optimized molecular structures of decarboxylation reaction of acetic acid.
Species Molecular Structure
B3LYP/6-31g(d) M06-2X/6-31g(d)
Decarboxylation Reaction:
R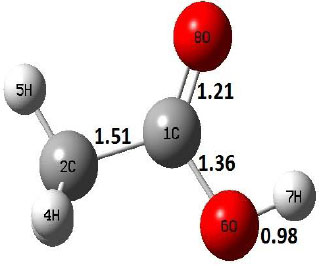
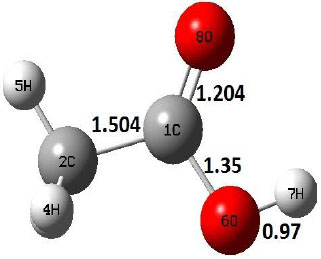TS1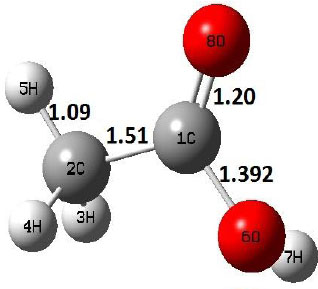
IM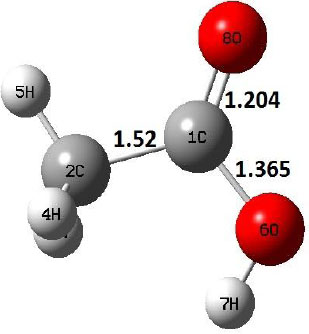
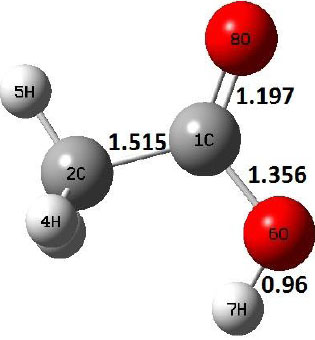TS2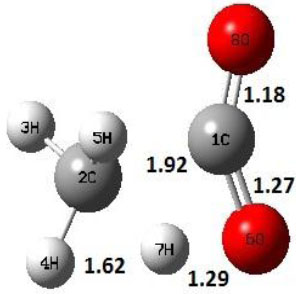
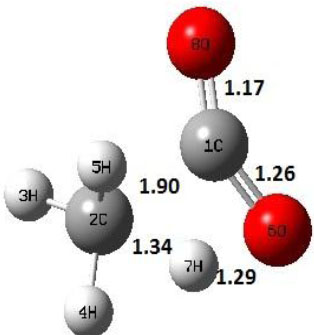P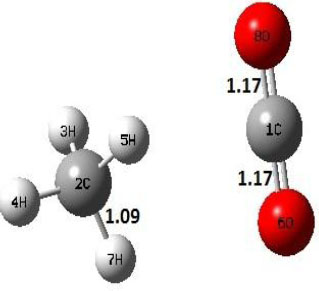

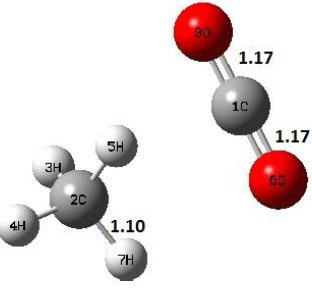3.1. Decarboxylation Reaction

Decarboxylation reaction of acetic acid (R) which produces methane and carbon di oxide molecules first undergoes the formation of a higher energy state, i.e., trans conformer of acetic acid (IM). In order to form the trans conformer, the torsional movement of 7H atom is carried out and can be seen in structures R, TS1, and IM of Table 1. In Fig. (1), blue and red coloured lines with square and triangle symbols show the decarboxylation reaction pathway at B3LYP/6-31g(d) and M06-2X/6-31g(d) level of theories, respectively. This one–dimensional minimum energy path is slice of the whole potential energy surface (PES). Quantitatively, it has only one coordinate (energy) but qualitatively, x–axis shows the reaction progress. Qualitatively, R progresses the reaction and forms TS1; however, quantitatively, TS1 has been optimized first followed by normal mode vibrational frequency analysis and an IRC calculation which linked its two minima in both directions as R and IM. The structures R and IM are true minima confirmed by another frequency analysis. Zero imaginary frequency in the frequency analysis of R and IM confirms the structures as true minima. The formation of trans-acetic acid occurs with 12.91 kcal/mol of barrier height given by B3LYP functional, whereas, same barrier height is reported as 12.43 kcal/mol by M06-2X functional. Further, the trans conformer of acetic acid produces carbon di oxide and methane molecule and, in order to get the actual product, a transition state TS2 in between IM and P has been optimized. The 7H atom of OH of –COOH functional migrates and forms a sigma bond with CH3 group and at the same time, cleavage of the C–O sigma bond occurs in order to form CH4 and CO2 molecules. The C=O bond distance in P is 1.17 Å; but the same bond distances in R and TS2 are 1.204 Å and 1.27 Å respectively. This is because in transition state search process molecule has to go through with inter-atomic stretching and bending until first order of energy gradient is not becoming zero in all the directions except any one. After donating hydrogen atom (7H), oxygen (6O) atom forms a double bond with carbon atom (1C) to produce CO2. Similar to prior process, an IRC calculation has been performed on the optimized transition state structure, TS2, to get the minima in both directions i.e., IM and P. The minima, IM and P, are the local minima with TS2 as the highest energy state in the minimum energy path of IM to P. This elementary reaction step, i.e., IM → P, is high kinetic demanding compared to previous reaction. It requires activation barriers of 63.38 kcal/mol and 66.72 kcal/mol due to B3LYP/6-31g(d) and M06-2X/6-31g(d) level of theories, respectively. Comparing the barrier heights of the decarboxylation reaction of M06-2X theory with the B3LYP theory; it is observed that M06-2X theory offers slightly higher energetics. The relative energies of IM and TS1 structures using M06-2X theory are 0.10 kcal/mol and 0.48 Kcal/mol higher compared to B3LYP theory. On the other hand, the relative energies of structures TS2 and P from M06-2X theory are 3.24 kcal/mol and 5.12 kcal/mol higher than B3LYP theory. The activation energy requirements by M06-2X theory for the first and second reaction steps are 12.43 kcal/mol and 66.72 kcal/mol, respectively, are under very good agreement with experimental work of Mackie et al. [9] and numerical work due to Duan et al. [10]. The M06-2X/6-31g(d) level of theory looks more similar like B3LYP theory but differs with slight changes in the bonding distances and energetics. This theory also follows the same reaction progress as of B3LYP theory. Comparing C=O bonding distances of carbon di oxide in TS2 of M06-2X functional with B3LYP theory, there are very minute change in distances. The changes in bonding distances of the structures due to M06-2X theory are in order of 10-2 – 10-3 with B3LYP theory for all involving structures in decarboxylation reaction.

Fig. (1). Reaction pathways of decarboxylation and dehydration reactions using both level of theories. Energies are with respect to R and in kcal/mol with ZPVE correction.

The Gibbs free energies at 298 K, 300–900 K with an interval of 100 K state that the cis to trans conformer reaction of acetic acid is not spontaneous for both level of theories at each studied temperature, whereas, the reaction between trans conformer of acetic acid to product (CH4 and CO2) is spontaneous reaction for both level of theories at all temperatures. Similarly, the enthalpy analysis shows that cis to trans conformer reaction and second reaction step of decarboxylation reaction of acetic acid are endothermic and exothermic reactions, respectively, at all temperatures up to 900 K.

3.2. Dehydration Reaction

The potential energy surfaces of dehydration reaction of acetic acid using both level of theories are depicted in Fig. (1); and the corresponding molecular structures, i.e., R, TS, and P, are shown in Table 2.

Table 2. The optimized molecular structures of dehydration reaction of acetic acid.
Species Molecular Structure
B3LYP/6-31g(d) M06-2X/6-31g(d)
Dehydration Reaction:
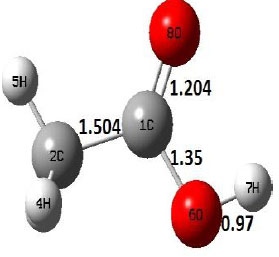
R
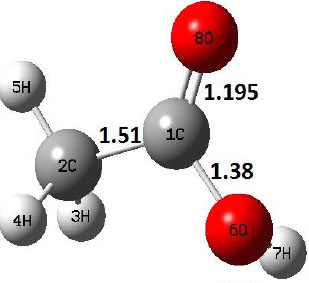
TS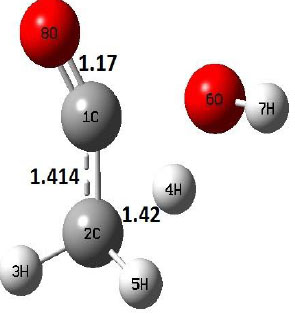
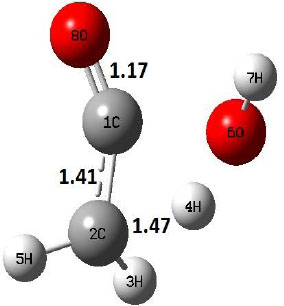P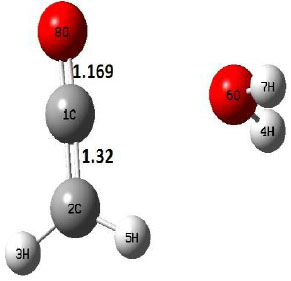

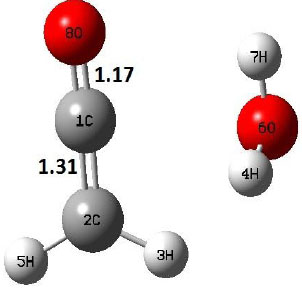The dehydration reaction proceeds from the cis structure of the acetic acid whereas the decarboxylation reaction, discussed earlier, proceeds with the trans structure of acetic acid. The PES of dehydration reaction involves only one transition state structure (TS) and it connects its both minima as P an R. The hydrogen atom of the methyl group of acetic acid forms sigma bond to OH of –COOH functional to produce water molecule. Then, after donating the hydrogen atom, methylene group (then methyl group) forms a double bond with the next carbon atom to produce ethenone. The activation barrier for this reaction using B3LYP/6-31g(d) level of theory is 75.86 kcal/mol. The relative energy of P is 40.49 kcal/mol with respect to R and this reaction is reported as an endothermic reaction. On the other hand, the relative energy of TS in M06-2X/6-31g(d) method is higher, i.e., 78.57 kcal/mol compared to the relative energy of TS due to B3LYP. Ruelle et al. [24] predicted the activation energy for this one step dehydration reaction of acetic acid as 78.4 kcal/mol which is in very good agreement with M06-2X/6-31g(d) level of theory. Duan et al. [10] predicted the activation energy for dehydration reaction of acetic acid as 76.4 kcal/mol which is in good agreement with B3LYP/6-31g(d) level of theory. The relative energy of the product of dehydration reaction, i.e., ethenone and water molecules, using M06-2X functional is 40.67 kcal/mol with respect to reactant’s energy, whereas, B3LYP functional shows the relative energy for this structure as 40.49 kcal/mol with respect to R. For dehydration reaction of acetic acid yielding ethenone and water molecules, the energetics don’t deviate significantly for product structure P comparing with both theories, whereas, the relative energies of P structures of decarboxylation reaction by both reported theories vary significantly. Comparing all molecular structures and reaction progress behaviours of M06-2X with B3LYP functional, both functionals do not deviate much in structural configurations but deviate a little in their energetics.

Using B3LYP functional at 298 K, the reaction free energy and reaction enthalpy of the dehydration reaction are reported as 39.16 kcal/mol and 41.90 kcal/mol respectively. The M06-2X/6-31g(d) level of theory predicts thermochemistry similar to B3LYP/6-31g(d) level of theory with little deviations, e.g., at 298 K, the reaction free energy and reaction enthalpy of dehydration reaction at M06-2X/6-31g(d) level of theory are 38.54 kcal/mol and 41.55 kcal/mol, respectively. However, at 900 K temperature using B3LYP functional, both thermodynamic parameters result in 31.65 kcal/mol and 44.14 kcal/mol respectively for dehydration reaction. On the other hand, at 900 K using M06-2X/6-31g(d) level of theory, the reaction free energy and reaction enthalpy are reported as 30.5 kcal/mol and 43.8 kcal/mol, respectively. Therefore, at 298 K using both level of theories, the dehydration reaction can be predicted as neither spontaneous nor exothermic reaction because of the very high positive energies of reaction free energy and reaction enthalpy. However, at elevated temperature, the reaction reaction constant (k) increases from 10-44 (298 K) to 10-6 (900 K) which means that there is an increase in reaction rate which is constructive in the context of reaction pace.

3.3. Kinetics

The reaction rate constants (sec-1) for the dehydration and decarboxylation reaction for both the theories are shown in Table 3. The linear plots of ln k versus 1/T for all reactions under each level of theory are shown in Fig. (2).

Table 3. Reaction rate constants of decarboxylation and dehydration reactions of acetic acid using both level of theories.
T (K) Decarboxylation Dehydration
B3LYP M06-2X B3LYP M06-2X
k1 (sec-1) k2 (sec-1) k1 (sec-1) k2 (sec-1) k3 (sec-1)
298 1.31E+03 1.71E-34 4.59E+03 6.40E-37 6.44E-44 8.83E-46
300 1.51E+03 3.46E-34 5.23E+03 1.34E-36 1.51E-43 2.16E-45
400 4.23E+05 1.69E-22 1.23E+06 2.53E-24 1.35E-29 5.82E-31
500 1.27E+07 1.84E-15 3.30E+07 6.18E-17 3.45E-21 2.84E-22
600 1.25E+08 9.39E-11 3.03E+08 5.37E-12 1.45E-15 1.84E-16
700 6.43E+08 2.23E-07 1.48E+09 1.84E-08 1.55E-11 2.70E-12
800 2.21E+09 7.66E-05 4.89E+09 8.41E-06 1.68E-08 3.69E-09
900 5.81E+09 7.31E-03 1.25E+10 9.93E-04 3.92E-06 1.03E-06

The k1 and k2 denote rate constants for first and second reaction steps, respectively, of the decarboxylation reaction of acetic acid. The first elementary reaction step of decarboxylation reaction is highly favourable reaction because of low activation energy and high rate constants in the order of 103-1010 sec-1 for both level of theories. At 298 K, the B3LYP/6-31g(d) theory report the rate constant as 1.31 Х 103 sec-1, whereas, M06-2X/6-31g(d) theory present this rate constant as 4.59 Х 103 sec-1. Similarly, at 900 K, k1 (B3LYP) and k1 (M06-2X) values are 5.81 Х 109 sec-1 and 1.25 Х 1010 sec-1, respectively. It is observed that the k1 (M06-2X) report higher values compared to the k1 (B3LYP). For the second step of the decarboxylation reaction of acetic acid, k2 values for both level of theories are also increasing with an increase in temperature (see Table 1). But, the second elementary reaction step of decarboxylation reaction is not likely to occur at 298 K because of very low rate constants. Further, increasing temperature improves reaction rate constants remarkably but even at 900 K, the rate constants k2 remain in the range of 10-3 and 10-4 sec-1 for B3LYP and M06-2X functionals, respectively.

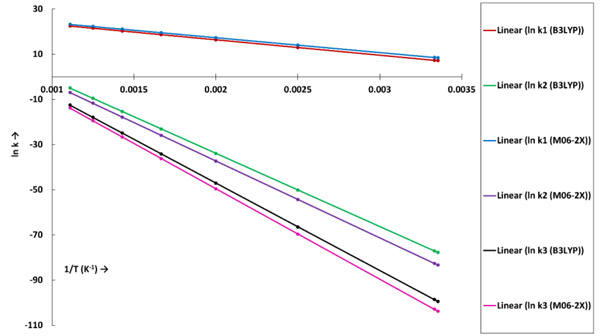Fig. (2). Plot of ln(k) vs. 1/T for decarboxylation and dehydration reactions of acetic acid using both level of theories.

The reaction rate constant of dehydration reaction of acetic acid is shown by k3 (see Table 3). The kinetic analyses of dehydration reaction using both level of theories suggest non-favourability of reaction because of much lower reaction rate constants. In addition, the values of k3 for dehydration reaction are much lower than k2 of decarboxylation reaction which suggests lower possibility of formation of ethenone and water molecules compared to the formation of methane and CO2. However, the rate constants of dehydration reaction are increasing with the temperature (see Table 1) for both level of theories but those remain close to zero even at 900 K which means reaction is not likely to occur.

The rate constant profiles of decarboxylation and dehydration reactions are linearly fitted for the values of ln k with respect to 1/T; and the plots of ln(k) vs. 1/T are shown in the Fig. (2) for both level of theories, i.e., B3LYP/6-31g(d) and M06-2X/6-31g(d). Blake et al. [7, 8] experimentally demonstrated that the decarboxylation reaction of acetic acid follows the first order reaction order for a temperature range of 530–1600 K. The profiles of ln(k) vs. 1/T are linear for all elementary reaction steps of decomposition reactions using both level of theories. Further, the Arrhenius relations are generated for each elementary reaction steps of decomposition reactions of acetic acid which are as follows:

(6) (7) (8) (9) (10) (11)

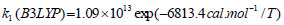
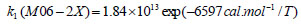
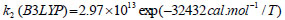
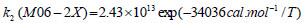
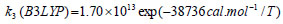
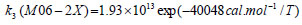
where reaction rate constants (k) are in sec-1 and temperatures (T) are in Kelvins.

CONCLUSION

The decomposition of acetic acid is performed using dehydration and decarboxylation reactions within the framework of density functional theory. Two competitive DFT functionals, i.e., B3LYP and M06-2X using 6-31g(d) basis set are employed for the analyses of barrier heights and reaction rate constants. The barrier heights for dehydration reaction are found as 75.86 kcal/mol and 78.57 kcal/mol for B3LYP and M06-2X functionals, respectively. The activation energies of decarboxylation reaction are 69.59 kcal/mol and 72.83 kcal/mol for B3LYP/6-31g(d) and M06-2X/6-31g(d) level of theories, respectively. These activation energies are in very good agreement with literature values. The kinetic analyses of decomposition reaction of acetic acid suggest non-favourability of both decomposition mechanisms in the temperature range of 298-900 K; however, decarboxylation reaction of acetic acid is slightly advantageous compared to dehydration reaction.

CONSENT FOR PUBLICATION

Not applicable.

CONFLICT OF INTEREST

The authors declare no conflict of interest, financial or otherwise.

ACKNOWLEDGEMENTS

Authors do not acknowledge any funding agency or any individual for this study.

REFERENCES

[1] G.W. Huber, S. Iborra, and A. Corma, "Synthesis of transportation fuels from biomass: chemistry, catalysts, and engineering", Chem. Rev., vol. 106, no. 9, pp. 4044-4098, 2006.
[2] H. Wang, J. Male, and Y. Wang, "Recent advances in hydrotreating of pyrolysis bio-oil and Its oxygen-containing model compounds", ACS Catal., vol. 3, pp. 1047-1070, 2013.
[3] C.A. Mullen, and A.A. Boateng, "Chemical composition of bio-oils produced by fast pyrolysis of two energy crops", Energy Fuels, vol. 22, pp. 2104-2109, 2008.
[4] M.T. Nguyen, D. Sengupta, G. Raspoet, and L.G. Vanquickenborne, "Theoretical study of the thermal decomposition of acetic acid: Decarboxylation versus dehydration", J. Phys. Chem., vol. 99, pp. 11883-11888, 1995.
[5] I.P. Moreira, "Performance of simplified G2 model chemistry approaches in the study of unimolecular mechanisms : Thermal decomposition of acetic acid in gas phase", J. Mol. Struct. THEOCHEM, vol. 466, pp. 119-126, 1999.
[6] C.H. Bamford, and M.J. Dewar, "The thermal decomposition of acetic acid", J. Chem. Soc., vol. 0, pp. 2877-2882, 1949.
[7] P.G. Blake, and G.E. Jackson, "The Thermal Decomposition of Acetic Acid", J. Chem. Soc. B, vol. 0, pp. 1153-1155, 1968.
[8] P.G. Blake, and G.E. Jackson, "High- and low-temperature mechanisms in the thermal decomposition of acetic acid", J. Chem. Soc. B, vol. 0, pp. 94-96, 1969.
[9] J.C. Mackie, and K.R. Doolan, "High-temperature kinetics of thermal decomposition of acetic acid and its products", Int. J. Chem. Kinet., vol. 16, pp. 525-541, 1984.
[10] X. Duan, and M. Page, "Theoretical investigation of competing mechanisms in the thermal unimolecular decomposition of acetic acid and the hydration reaction of ketene", J. Am. Chem. Soc., vol. 117, pp. 5114-5119, 1995.
[11] A.D. Becke, "Density-functional thermochemistry.III. The role of exact exchange", J. Chem. Phys., vol. 98, pp. 5648-5652, 1993.
[12] R.G. Parr, and Y. Weitao, Density-Functional Theory of Atoms and Molecules., Oxford University Press, 1994.
[13] Y. Zhao, and D.G. Truhlar, "The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other function", Theor. Chem. Acc., vol. 120, pp. 215-241, 2008.
[14] Y. Zhao, and D. G. Truhlar, "Density functional for spectroscopy: No long-range self-interaction error, good performance for Rydberg and charge-transfer states, and better performance on average than B3LYP for ground states", J. Phys. Chem., vol. 110, pp. 13126-13130, Novermber 2006.
[15] P. Hohenberg, and W. Kohn, "Inhomogeneous electron gas", Phys. Rev., vol. 136, pp. B864-B871, 1964.
[16] W. Kohn, and L. Sham, "Self-consistent equations including exchange and correlation effects", Phys. Rev., vol. 385, pp. A1133-A1138, 1965.
[17] F. Jensen, Introduction to Computational Chemistry., 2nd edJohn Wiley & Sons Ltd., 2007.
[18] R. Ditchfield, W.J. Hehre, and J.A. Pople, "Self Consistent Molecular Orbital Methods. IX. An Extended Gaussian Type Basis for Molecular‐Orbital Studies of Organic Molecules", J. Chem. Phys., vol. 54, pp. 724-728, 1971.
[19] W.J. Hehre, R. Ditchfield, and J.A. Pople, "Self—Consistent molecular orbital methods. XII. further extensions of gaussian—type basis sets for use in molecular orbital studies of organic molecules", J. Chem. Phys., vol. 56, pp. 2257-2261, 1972.
[20] H.P. Hratchian, and H.B. Schlegel, "Accurate reaction paths using a Hessian based predictor-corrector integrator", J. Chem. Phys., vol. 120, no. 21, pp. 9918-9924, 2004.
[21] M.J. Frisch, G.W. Trucks, H.B. Schlegel, G.E. Scuseria, M.A. Robb, J.R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G.A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H.P. Hratchian, A.F. Izmaylov, J. Bloino, G. Zheng, J.L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J.A. Montgomery, J.E. Peralta, F. Ogliaro, M. Bearpark, J.J. Heyd, E. Brothers, K.N. Kudin, V.N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J.C. Burant, S.S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J.M. Millam, M. Klene, J.E. Knox, J.B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R.E. Stratmann, O. Yazyev, A.J. Austin, R. Cammi, C. Pomelli, J.W. Ochterski, R.L. Martin, K. Morokuma, V.G. Zakrzewski, G.A. Voth, P. Salvador, J.J. Dannenberg, S. Dapprich, A.D. Daniels, Ö. Farkas, J.B. Foresman, J.V. Ortiz, J. Cioslowski, and D.J. Fox, Gaussian 09, Revision B.01., Gaussian, Inc.: Wallingford, CT, 2009.
[22] R. Dennington, T. Keith, and J. Millam, GaussView, Version 5., Semichem Inc.: Shawnee Mission, KS, 2009.
[23] H. Eyring, "The activated complex in chemical reactions", J. Chem. Phys., vol. 3, pp. 107-115, 1935.
[24] P. Ruelle, "Ab initio quantum-chemical study of the unimolecular pyrolysis mechanisms Of acetic acid", Chem. Phys., vol. 110, pp. 263-274, 1986.