Modeling an Airlift Reactor for the Growing of Microalgae

All published articles of this journal are available on ScienceDirect.

RESEARCH ARTICLE

Modeling an Airlift Reactor for the Growing of Microalgae

Gustavo A. Lara1 Luis Moreno2 , 3 Yendery Ramírez2 , 4 Luis A. Cisternas2 , * Open Modal
Authors Info & Affiliations
The Open Chemical Engineering Journal • 28 Sep 2018 • RESEARCH ARTICLE • DOI: 10.2174/1874123101812010080

Abstract

Objective:

The flow dynamics of an airlift reactor for the growing of microalgae is modeled using Computational Fluid Dynamics (CFD). The model is applied to the operation and optimization of the reactor, giving a valuable picture of the liquid movement and carbon dioxide trajectory at different air injection flow rates.

Methods:

A novel aspect of the model is that air and carbon dioxide are injected at separated locations. Air is injected at the bottom of the reactor and CO2 injection takes place in the downcomer region of the reactor to obtain longer CO2 paths, improving its transference.

Results:

The results show modeling is a useful tool in the control of the reactor operation; for example, in avoiding the sedimentation of microalgae or for detecting the existence of zones with extremely low CO2 concentrations.

Keywords: Photo-bioreactor, Microalgae, Biofuel, Modeling, CFD, Fluent, Bubble column reactor.

1. INTRODUCTION

Bubble column reactors are widely used in the chemical and biochemical industries due to their high mass and heat transfer rates [1]. These reactors are usually formed by a cylindrical or rectangular vessel which has an air injection at the bottom, causing the generation of bubbles [2-6]. In this type of reactor, the flow is completely driven by gravity [7]. Because these reactors do not have moving parts, the maintenance and operation costs are small [3, 4, 6, 8]. An important application for bubble column reactors is in bioreactors that grow microorganisms [9-12], which are used in the production of valuable industrial products. An example of these bioreactors includes the photo-bioreactors used for the growth of microalgae, which are used as a raw material in the production of biodiesel.

An important process in a photo-bioreactor is the absorption of solar energy [13-15], which may occur by using a device to concentrate the solar radiation or, as in our case, by the direct absorption of solar radiation. To distribute the radiation in a uniform way, microalgae need to be maintained in continuous motion. Agitation is useful to improve the mass transfer between the microalgae and the liquid and to avoid the deposition of microalgae at the reactor bottom [5], [16, 17]. In most cases, the agitation is performed using an air bubbly system, since mechanical agitation could damage the microorganisms. The growth of microalgae requires the addition of carbon, which may be added by means of solutions of carbonate or bicarbonate, or as CO2 gas injected mixed with the air used for agitation or as small gas bubbles in a different location to that used by the air injection. The latter method is used in this work. The optimization and control of algae growth are of vital importance in improving the process from technical and economic perspectives [18]. Simulations are used to optimize the design and its operation.

The hydrodynamic behavior of the bioreactor is crucial for its satisfactory operation [2-4, 6, 19-24]; it should include a uniformly distributed absorption of the solar radiation, a high mass transfer, and the microalgae permanently suspended in the alga-liquid mixture. Therefore, the understanding of these mechanisms is of vital importance in the design and operation of photo-bioreactors. The modeling of the three-phase system formed by the alga-water mixture, the air bubbles, and the CO2 bubbles may be performed in different ways depending on the objective, as well as on the software availability.

Several models exist for bioreactors [2, 3, 23-30], but due to their complexity they are used only for specific problems, or important simplifications would need to be introduced to obtain solutions in a suitable timeframe. For instance, a compartment photo-bioreactors model exists which includes fluid dynamics, mass transfer, and algae growth kinetics [31]. However, due to its complexity, the model is first solved for the flow field and the system is then divided into large compartments; the resulting compartment model is then finally solved. Another existing model is one for microalgae growth and lipid production [32]. To solve this model, it is assumed that no coupling exists between growth and photosynthesis when the nitrogen is depleted. In another work [33], a three-phase photo-catalytic reactor is modeled, in which the coupling in the reactor is carried out through the equation for radiation. It is assumed that the overall reaction rate is directly proportional to the local volumetric rate of energy absorption.

Computational Fluid Dynamic (CFD) modeling using the software Fluent [26, 28, 30, 33, 34] has been widely applied in mechanical and chemical engineering as a valuable tool, not only to understand fluid dynamics but also to reduce associated costs [34, 35].

For the numerical solutions of the models, some simplifications may be applied depending on the flow conditions. For example, in a system with low Reynolds numbers, such as the liquid in bubble column reactors, a Large Eddy Simulation (LES) may be more suitable for describing the liquid motion [36, 37] than the Reynolds-averaged Navier-Stokes equations [38]. A comparison of both approaches found that the two models are in agreement. The Algebraic Slip Mixture (ASM) model assumes that slip can be modeled using a simple algebraic formula, and this can simplify the full multiphase flow model. The ASM model is implemented using Fluent software [39]. Fluent is also used for simulating the ferrous bio-oxidation in a bubble column reactor, combining the hydrodynamics with kinetics [40]. In another work, CFX software was used for studying the flow pattern in a bubble column reactor and compared the k-ε model with the Reynold Stress Model (RSM), finding that both give similar results [41].

In airlift reactors used for the growing of microalgae, air bubbles are injected at a section of the bottom for the purpose of maintaining the fluid in movement and avoiding the sedimentation of the microalgae [16, 17, h19-23]. The movement of the fluid homogenizes the system, allowing uniform absorption of the radiation and removing the oxygen and other gases from the system. In these reactors, the introduction of carbon dioxide is required for the growth of the algae, which is dissolved in the liquid and consumed by the microalgae. Carbon dioxide is usually introduced together with the air, forming a mixture; however, this is not a convenient technique since different bubble sizes would ideally be used for the air and carbon dioxide to improve the system. The air should be introduced using bubbles of a size that is sufficiently large to obtain high enough rise velocities for generating a good mixing of the liquid. On the other hand, carbon dioxide should be injected as small bubbles to increase the transference of CO2 from the bubble into the water; the mass transfer rate is proportional to the bubble specific area, which is inversely proportional to its diameter. Since the biological conditions change with time, the model is focused on the hydrodynamics of the system and the results are combined with microalga parameters obtained from the literature, such as the activity, density, and particle size. In the bubbly flow regimen of a down-flow jet loop reactor, various hydrodynamic parameters have been characterized [42]; experiments were carried out studying the gas holdup, bubble sizes and distribution, mass transfer area, and mass transfer coefficient. A multipurpose laboratory apparatus was developed for the optimization of the microalgae experimental conditions [43]. Using this apparatus, the influence on the process variables such as the temperature, CO2 concentration, and radiation was evaluated.

The use of algae as a raw material in the production of valuable substances requires a reduction of the associated costs. This is particularly valid when they are used for biodiesel production, in order to be competitive with other energy sources and because biodiesel profitability is sensitive to biomass production costs [44]. CFD-based modeling provides a solid method for optimizing the algae production.

The aim of this paper is to develop a model to be used in the operation and optimization of reactors used in the growing of microalgae; for example, those used for biodiesel production. The model should provide a clear picture of the hydrodynamics of the reactor and the carbon dioxide trajectory as a function of the air-injection flow rate. This would facilitate the control of the operation of the reactor, avoiding the sedimentation of the microalgae and the existence of zones with extremely low CO2 concentration. The satisfactory operation of an air bubbly reactor would be characterized by the maintenance of a uniform distribution of the microalgae in the reactor, and long paths for the carbon dioxide bubbles to increase the mass transfer of CO2 into the liquid.

2. MATERIALS AND METHODS

2.1. Reactor Geometry and Meshing

The primary motivation of this paper is the simulation of photo-bioreactors for the growth of microalgae used as a raw material in the production of biodiesel. The reactors are built using polyethylene bags supported by a metallic structure, as shown in Fig. (1).

Fig. (1). Photo-bioreactor used in the growth of microalgae for the production of biodiesel.

The modeled reactor is a rectangular box with dimensions of 1.5 m in height, 1.0 m in width, and 0.25 m in depth, as shown in Fig. (2). For the CFD model, an unstructured mesh is used with the computational domain discretized in 136813 elements.

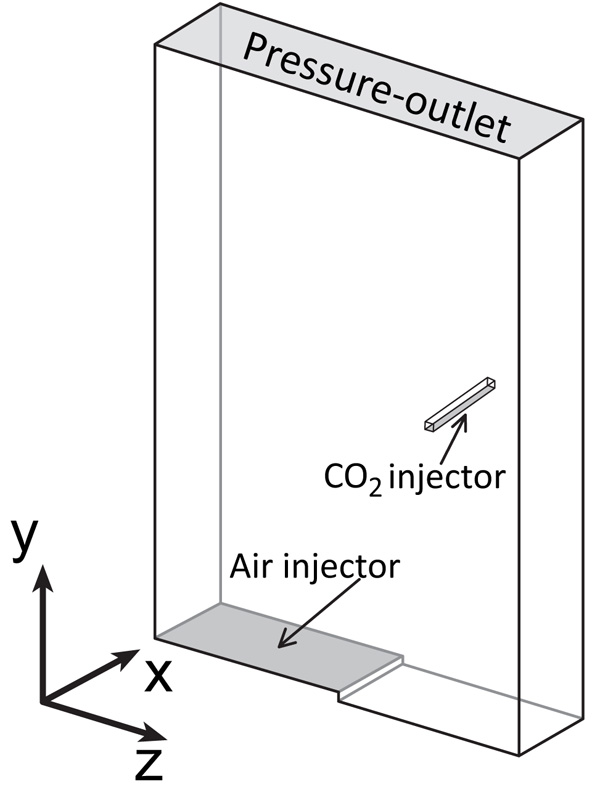
Fig. (2). Reactor geometry. Dimensions 1.5 m×1.0 m×0.25 m.

The air-injector is located at the bottom of the reactor and has a length of 0.50 m. It is adjusted to the left side at a distance of 0.01 m from the bottom, constituting an internal-loop airlift reactor. The injection of carbon dioxide occurs through a rectangular tube located at 0.75 m height and 0.25 m from the right wall in the downcomer region. This location is chosen to obtain longer paths for the CO2 before leaving the reactor, improving the mass transfer of CO2 into the liquid. The shape and direction of the diffuser of the CO2 were chosen to reduce interference with the liquid flow and to obtain a homogeneous injection of CO2.

2.2. Modeling

Several types of modeling exist. The most complex models are used when we are interested in how the locations of specific bubbles change with time. In this case, the Navier-Stoke equations are applied for the liquid and bubbles in detail. When the location of the given bubbles is not important, as in our case, the model calculates the average volume fraction occupied by the gas phases instead of determining the location of each phase in detail [45].

We use the Multiphase Eulerian model with three phases: a) the water phase, b) the air-bubbles phase, and c) the CO2-bubbles phase. Therefore, three different velocity-fields are considered; one for each phase. They are solved for the velocity-fields, the pressure, and the gas-volume fractions. To solve the model, Fluent 14.5.7 software is used. The three phases are treated as interpenetrating continua and are described by phasic volume fractions. The inlet boundary conditions are the inlet air velocity and the inlet CO2 mass rate. The outlet boundary condition is the pressure (atmospheric) at the top of the bioreactor, without backflow of gases, but with backflow of liquid. The implicit scheme is used to solve the model.

The primary phase (water including microalgae) is the continuous phase with an assumed temperature of 25 ºC, and with a density of 998.2 kg/m3 and viscosity of 0.001 kg/(m s). Since the microalgae concentration is small, it was assumed that the properties of the mixture (microalgae-water-bubbles) are similar to those of the water. The secondary phases are air and CO2 bubbles with Sauter mean diameters of 10 mm and 0.5 mm, respectively. Photographing was used for determining the diameter of the air bubbles in the reactor. From these photographs, which show a narrow size distribution, the mean bubble diameter was estimated. A similar technique was used for the CO2 particles, but its determination presents larger measurement error due to the small diameter of the bubbles.

In the Viscous Model we consider turbulence for a single-phase fluid, which is a mixture of the three phases, and apply the RNG k-ε model with near-wall scalable wall functions using the differential viscosity model, swirl dominated flow, and curvature correction. The effectiveness of the RNG model is achieved for both high and low Reynolds numbers. The mass and momentum conservation equations, together with the turbulence RNG k-ε model, are shown in Appendix.

2.3. Modeled Cases

The most important process for a given reactor’s geometry is the injection of air, because this controls water circulation and its agitation in the reactor. Air injection determines the occurrence of alga sedimentation, the distribution of the carbon-dioxide bubbles, the transference of CO2 into the water, and the removal of the oxygen produced by the algae. Low air injection flow rates imply low water circulation rates that may cause microalga sedimentation, low CO2 transfer rates into the water, and insufficient oxygen removal. However, high injection flow rates have a high-energy cost, and the CO2 bubbles may not have sufficient time to dissolve in the liquid before they leave the reactor. In the simulations, the air injection flow rate was varied within a wide interval-from 0.5–60 L/min. The main parameters used in the simulations are shown in Table 1.

Table 1.
Main parameters used in the simulations.
Entity Value
Air injection flow rate, L/min 0.5–60.0
Air bubble diameter, mm 10
CO2 injection mass rate, g/h 5
CO2 bubble diameter, mm 0.5

The mass transfer of CO2 from the bubbles into the liquid is complex since it is determined by the mass transfer coefficient, the concentration of CO2 in the liquid at the bubble surface, and the concentration of CO2 in the liquid bulk. The two first entities may be directly addressed: the mass transfer coefficient is determined by the liquid properties and the relative velocity between the bubbles and the liquid, while the CO2 concentration in the liquid, at the bubble surface, is given by the CO2 solubility in water. However, the CO2 concentration in the liquid bulk is determined by the balance between the CO2 mass-transfer rate from the bubbles into the liquid and the CO2 consumption rate by the microalgae, which depends on several factors such as the number of microalgae, the radiation absorption rate, and the existence of nutrients. The CO2 mass transfer rate is small when the number of microalgae is small since this causes an increase in CO2 concentration in the liquid phase, decreasing the driving force for the mass transfer. In the opposite situation, a high number of microalgae decreases the concentration of CO2 in the liquid, increasing the mass transfer due to the higher driving force.

In this work, the microalgae activity is not modeled; therefore, experimental values from the literature are used. In this particular work values obtained for the growing of the algae Botryococcus braunni were used [46]. The production mass rate of 0.114 g/L/d of dry biomass was reported; since 1 kg of dry algal biomass needs about 1.83 kg CO2, the mass transfer from the CO2 phase to the liquid phase must be 0.209 g/L/d [47]. The bioreactor in our case has a volume of 374 L and is fed with CO2 bubbles at a mass rate of 5 g/h, so that on average the injection rate per unit volume is 0.32 g/L/d. This injection mass rate is about 50% greater than the CO2 consumption for conditions like those of the algae Botryococcus braunni. Therefore, similar experiments are required in each case. The mass transfer rate per unit volume is, where is considered a constant throughout the reactor volume, and its value can vary from zero when the water is saturated with CO2 due to the low population of microorganisms, up to a maximum that depends on the capacity of CO2 capture by the algae. We have used the value = 4 10-5 s-1, with which it is possible to reach mass transfer rates similar to the algae Botryococcus braunni [46].

3. RESULTS

The system was modeled for different air injection flow rates. Because the system is turbulent, the results may be shown as a picture taken at a given instant of time, or as an average value during a certain time interval. Fig. (3) shows the water velocity vector at a given instantaneous time for an air injection of 5 L/min. The water rotates clockwise approximately in a vertical plane due to the air injection being in the reactor bottom, through a perforated plate located in the left half. Therefore, the liquid flows upward along the left side of the reactor and downward along the opposite side. At the bottom and top of the reactor, the flow is mainly horizontal-from the right to the left at the reactor bottom, and in the opposite direction at the top. The velocities perpendicular to the main plane of the reactor are smaller.

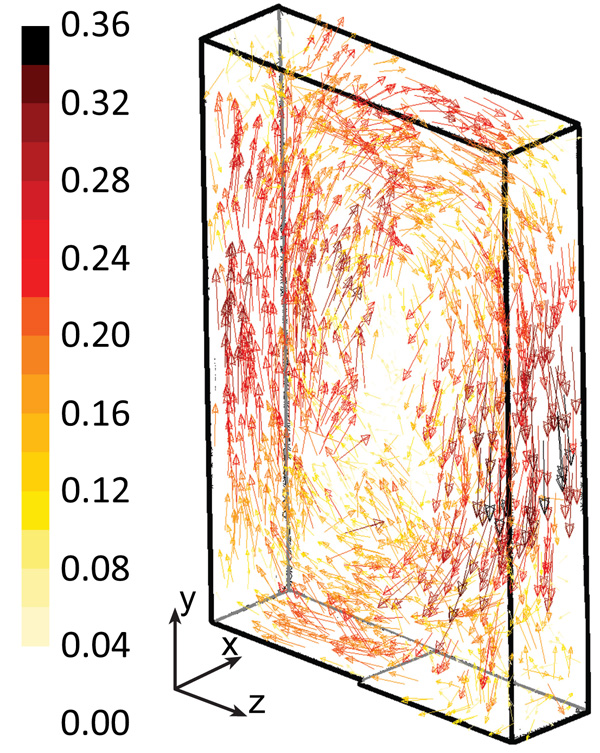
Fig. (3). Water velocity vector (m/s) for an air injection flow rate of 5 L/min.

The flow pattern in the reactor may be also visualized by plotting the velocity magnitude or the velocity components. Fig. (4) shows the water-velocity magnitude averaged on a time interval of 600 s, for an air injection flow rate of 5 L/min. High water velocities are mainly grouped along the vertical walls (left and right sides) at half height. In addition, relatively high velocities are found at the central part of the reactor’s top and bottom. The instantaneous water velocity (not shown) is more asymmetric when compared with the average values, since the averaging-process smooths the velocity. Turbulence plays an important role in some circumstances since the water does not flow in a plane, however, the component of the velocity that is perpendicular to the main plane (x-axis) is not negligible, which increases the agitation in the reactor. The instantaneous water velocity along the x-axis varies notably, reaching large values in both directions-from 0.14 m/s in one direction to 0.14 m/s in the opposite direction. These velocity values of 0.14 m/s correspond to about 50% of the maximum velocity magnitude. However, the x-velocities averaged at a time of 600 s are very small; most values are less than 0.02 m/s. Therefore, large differences are observed between the instantaneous and averaged velocities along the x-axis.

This shows the importance of considering turbulence, since large instantaneous water velocities are found in both directions along the x-axis; in spite of this, the average velocities are very small along this axis. If turbulence were neglected the model would be a poor description of the reality, specifying an agitation much smaller than that observed in the actual model. This also emphasizes the importance of using 3-D modeling for this type of system. The use of 2-D modeling is not adequate because it ignores the mixing in the x-direction caused by the turbulence, which improves the mass transfer in the reactor. In the y- and z-direction, turbulence is less important since advective forces dominate the water flow.

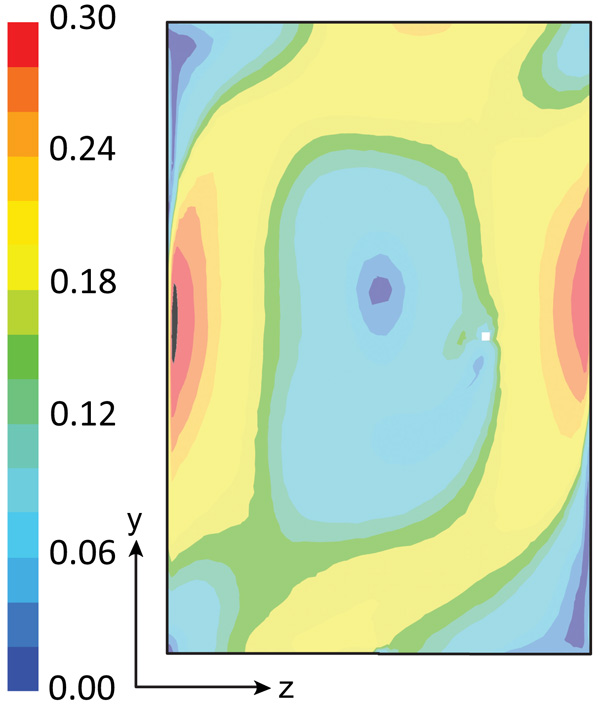
Fig. (4). The magnitude velocity (average) in m/s at the middle plane for an air injection flow rate of 5 L/min.

The carbon dioxide gas is injected 25 cm from the right wall and at a height of 75 cm. Since the injection of CO2 is done in the downcomer zone, the gas bubbles have long trajectories before they leave the reactor through the top. Therefore, more gas is dissolved into the liquid in the reactor. The trajectory of the gas bubbles is determined by a force balance between the upward buoyant force on the gas bubbles and the drag force of the flowing water around the gas bubbles. If the water velocity is very small, the gas bubbles may escape directly to the top of the reactor and be lost to the atmosphere. However, if the water velocity is extremely high the gas bubbles follow the water flow, showing long trajectories before they reach the top of the reactor. In this case, the contact time between the gas bubbles and the liquid will be very short due to the high-water velocity, and only a small amount of CO2 will be transferred from the gas bubbles into the liquid.

Fig. (5) shows the CO2 concentration profile, expressed as a volume fraction at the middle plane of the reactor for values averaged at a time of 600 s. Very high concentrations are observed around the injection device. However, high carbon dioxide values are also observed at the center of the reactor (volume fractions of about 0.0001) while in other zones, the volume fraction is several orders of magnitude lower. Low CO2 concentrations are observed at the top and bottom of the reactor and very low values in locations close to the left wall. The CO2 volume fraction close to the right wall is relatively high. The scale is logarithmic because the concentration of CO2 in the reactor varies by several orders of magnitude. For example, locations close to the left wall show volume fractions approximately three orders of magnitude less than the values in the central part of the reactor. Some critical zones exist in which the CO2 concentration is extremely low, such as at the lateral edges at the reactor bottom. Therefore, edges-where the planes intersect perpendicularly-should be avoided. Rounded edges should be used in these locations if possible, because low CO2 concentrations dominate in zones with stagnant water.

Fig. (5). CO2 volume fraction (average) in the middle plane for an air injection flow rate of 5 L/min.

Another aspect that was studied was the coalescence and break of the bubbles. A bubble size distribution exists for the bubbles emerging from the sparger. However, in the simulations, a constant bubble diameter was assumed, which is specified by an experimental correlation [48]. Therefore, one question that can arise is whether the phenomena of coalescence and bubble breaks are important. We performed simulations using Population Balance Modeling with discrete inhomogeneous phases [49]. Bubbles were injected with a specified diameter of 10.0 mm and 0.5 mm for air and CO2, respectively. The results show that coalescence and break are insignificant for the air and CO2 bubbles.

4. DISCUSSION

4.1. Impact of the Air Injection Flow Rate on the Water Velocity Distribution

The determining factor in the movement of the microalgae is the difference between the water velocity and the microalgae sedimentation velocity. If the water velocity is significantly greater than the sedimentation velocity, the microalgae follow the water flow. The microalgae sediments if the water velocity is smaller than the sedimentation velocity. This velocity is specific for each microalga type and depends on its size and density. To maintain the problem independent of the microalgae type, the calculations are reported for several sedimentation velocity levels (from 0.02–0.10 m/s) and, therefore, these results could be applied to different microalgae.

The water velocity distribution in the reactor is addressed by determining the fraction of the reactor volume with a water velocity higher than a certain value for different air injection flow rates. Fig. (6) shows the reactor volume fraction with water velocities higher than 0.02, 0.04, 0.06, 0.08, and 0.10 m/s for different air injection flow rates. For example, if a water velocity of 0.06 m/s is required in the reactor to avoid alga sedimentation, only 65% of the reactor volume will show velocities greater than 0.06 m/s for an air injection flow rate of 1 L/min (35% of the reactor volume algae may sediment). To reach 90% of the reactor volume with a water velocity greater than 0.06 m/s, the air injection flow rate would need to be about 3 L/min. It is also shown that, for an air injection flow rate greater than 10 L/min, the fraction of the reactor volume with a velocity greater than a given value is only slightly improved when the air injection flow rate is increased.

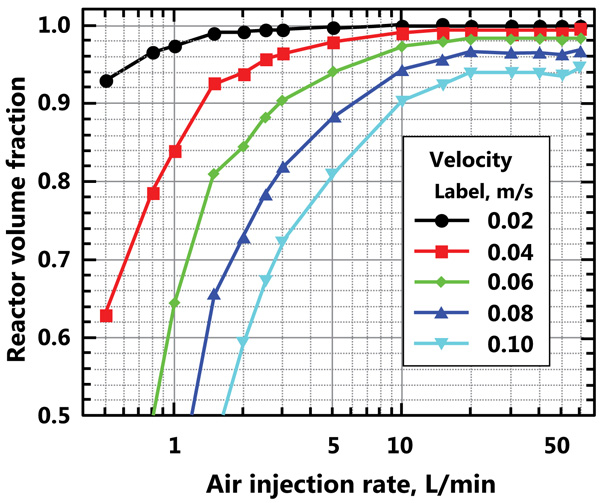
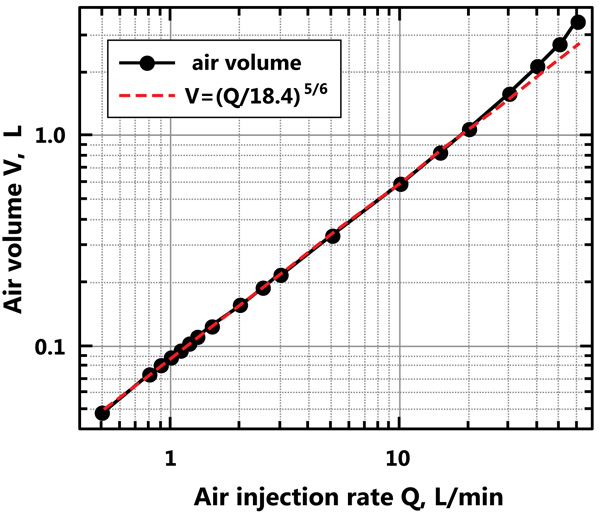
Fig. (6). Reactor volume fraction with a water velocity higher than a given level for different air injection flow rates.

The volume fraction of the air bubbles in the reactor, as a function of the air injection flow rate, was determined. A power relationship was fitted to the resulting data;, where is the air volume fraction in the reactor and Q is the air injection flow rate in L/min. Considering that the volume of the reactor is 374 L, the air volume in the reactor may be determined. Fig. (7) shows the volume of the air bubbles in the reactor and the fitted curve. The residence time of the air in the reactor is then calculated; this varies from approximately 6 s for an air injection flow rate of 0.5 L/min to approximately 3.5 s for an air injection flow rate of 60 L/min.

Fig. (7). The volume of air in the reactor as a function of the air injection flow rate.

4.2. Impact of the Airflow Injection Flow on the Carbon Dioxide Distribution

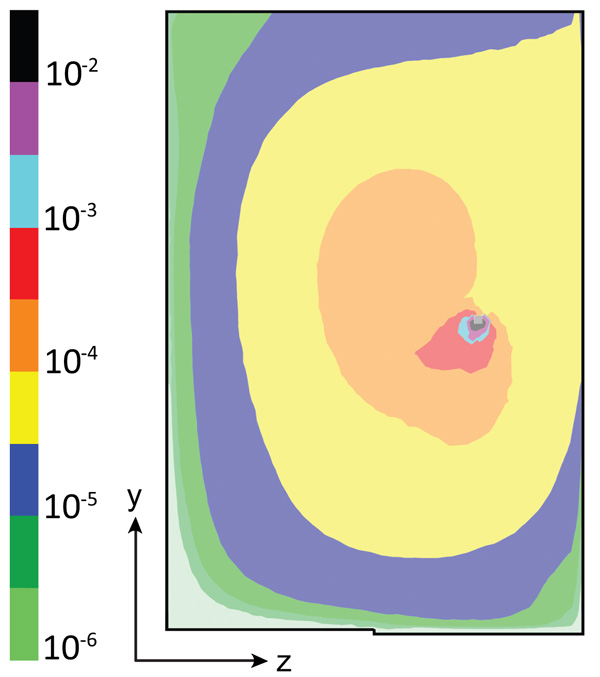
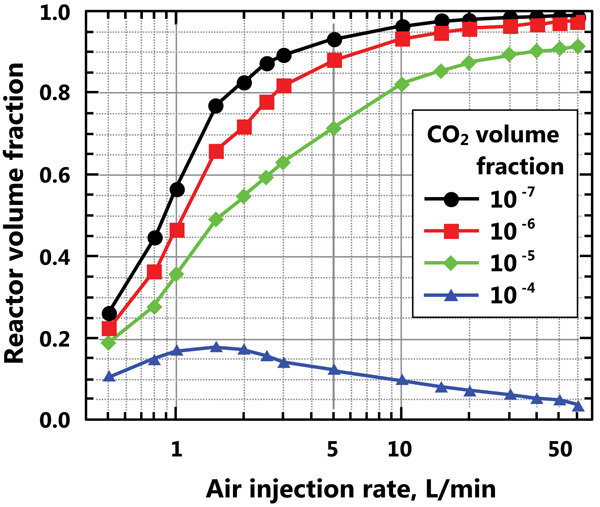
In the simulations, the injection flow rate of CO2 was maintained as a constant, and only the air injection flow rate (the agitation) was varied (from 0.5-60 L/min). For a very low air injection flow rate, the CO2 bubbles were concentrated in some zones of the reactor and very low CO2 concentrations were observed in large zones. Fig. (8) shows the reactor volume fraction where the carbon dioxide concentration is higher than a given level. For the lowest air injection flow rate (0.5 L/min), approximately 80% of the reactor volume shows negligible CO2 concentrations. By increasing the air injection flow rate, the extent of the zone with low CO2 concentration is significantly decreased; for instance, for an air injection flow rate of 5 L/min, 72% of the reactor volume achieves CO2 concentrations higher than 10-5, and only 12% of the reactor has CO2 concentrations less than 10-6. The curve for a volume fraction of 10-4 shows a different pattern, since this corresponds to very high concentrations which are obtained only around the CO2 injector.

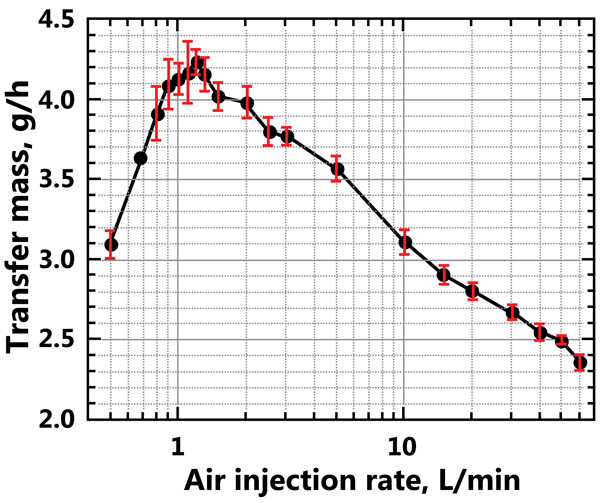
Fig. (8). Reactor volume fraction with a carbon dioxide concentration higher than a given level.

The mass transfer from the CO2 bubbles into the liquid is shown in Fig. (9). The transference of CO2 is small for the two extreme cases: for the lowest air injection flow rate and for the highest air injection flow rate, as shown in the figure. At the lowest air injection flow rate the paths for the CO2 bubbles are the shortest, while for the highest injection flow rate the residence time for the CO2 bubbles is the shortest; both conditions cause small CO2 mass transfer rates. For the conditions used in the simulations, the maximum mass transfer rate of CO2 into the water is 4.2 g/h for an air injection flow rate of approximately 1-2 L/min. The mass transfer rate decreases to a value of 2.4 g/h for the highest air injection flow rate of 60 L/min. The average residence time of the CO2 bubbles is determined by the mass of CO2 in the reactor and the CO2 injection mass rate, the latter of which is constant in these simulations and has a value of 5 g/h. The mass of CO2 in the gas bubbles is 0.029 g for the highest air injection flow rate, and 0.052 g for the maximum mass transfer rate of CO2. Therefore, the residence time for the CO2 is 21 s for the highest air injection flow rate used in the simulations (60 L/min) and 37 s for the maximum mass transfer rate of CO2, which occurs at an air injection flow rate of approximately 1–2 L/min. The injection of CO2 in the downcomer region increases the CO2 residence time by a factor of approximately six compared with injecting the CO2 with the air. Therefore, the CO2 injected in this distinct location is dissolved into the water phase to a larger extent.

Fig. (9). The carbon dioxide mass transfer rate from the CO2 bubbles into the water in the reactor for different air injection flow rates.

CONCLUSION

The aim of this work was to develop a model for the optimization of the operation of photo-bioreactors used for growing of microalgae, in which agitation and the accessibility of the carbon source are the most important factors (in addition to the solar radiation). This paper focuses on the hydrodynamics of the reactor in order to ensure adequate agitation and good access to CO2 in most parts of the reactor.

The simulations show that water circulates in a wide swirl in the reactor main plane. Low water velocities are found in the reactor center and at the reactor’s four lateral edges. The low water velocities at the lateral edges at the reactor bottom are critical because the microalgae could sediment at these locations. However, low water velocities in the reactor’s center and top are not important because, if sedimentation occurs, microalgae will encounter high water velocities during the sedimentation process. The lateral edges at the reactor bottom could be rounded to avoid low water velocities in these zones, however, the cost of the process must be kept low because microalgae for biodiesel are relatively low value and have economic difficulties in competing with other energy sources. On the other hand, if the reactor were used for the growing of other microalgae with a higher worth, the economic situation would be more favorable to the investment in a change of geometry to avoid zones where algae may deposit.

The physical characteristics of the microalgae (size and density) and liquid viscosity determine the lowest limit for the air injection flow rate in order to avoid or reduce the sedimentation. Therefore, the sedimentation velocity sets the lowest limit for the air injection flow rate.

The instantaneous velocities perpendicular to the reactor’s main plane (x-axis) show large values and large variations. This shows that turbulence plays an important role in the movement of microalgae in the reactor, which increases the mass transfer between the microalgae and the water. This also shows that simulations should be carried out in 3-D since important information would be lost if a 2-D system were used. The average velocities in this direction are very small; therefore, instantaneous velocities should be considered when the effect of turbulence is considered. For velocities in the other directions, no large differences exist between the instantaneous and average velocities since they are mainly determined by advective forces and turbulence is less important.

Injecting the CO2 in a distinct location at the downcomer region significantly increases the transference of carbon dioxide into the water phase. For the values used in the simulations, the residence time for the CO2 is increased by a factor of about six when compared with the injection of CO2 together with the air. The residence time for the air in the reactor is in the range of 3.5–6 s, while the residence time for the CO2 is between 21-37 s. Therefore, separation of the air injection and CO2 injection is more efficient because the residence time of the CO2 bubbles in the reactor significantly increases, thus improving the mass transfer of CO2 into the liquid phase. Injecting air with very small or very large flow rate leads to a decrease of CO2 transfer in the reactor. Therefore, the optimal air-injection flow rate could be determined in each case. The location of the CO2 injection was chosen to maximize the CO2 transference; in this zone the water goes down, ensuring a long path for the CO2 in the reactor which in turn increases the CO2 residence time in the reactor.

CONSENT FOR PUBLICATION

Not applicable.

CONFLICT OF INTEREST

The authors declare no conflict of interest, financial or otherwise.

ACKNOWLEDGMENTS

The authors wish to thank CONICYT for support through the projects MEL 81105010, ACT 1201 and Fondecyt 1180826.

APPENDIX

Governing Equations

Mass Conservation Equation

The continuity equations are:

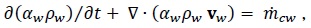(1)
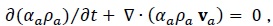(2)
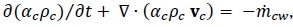(3)

where 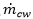is the mass transfer from CO2 bubbles into the water.

Momentum Conservation Equations

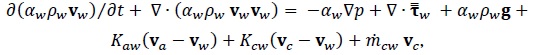(4)
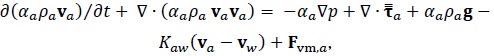(5)
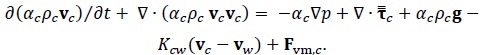(6)

Turbulence RNG k-ε Model

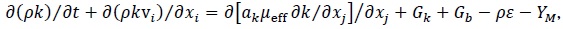(7)
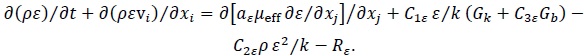(8)

Where

Fvm,i   Virtual mass force on phase i N/m3
g   Gravity vector m/s2
k   Turbulent kinetic energy m2/s2
Kij   Interphase exchange momentum coefficient between i and j phases Pa s/m2
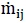  Mass transfer between i and j phases kg/s/m3
p   Pressure Pa
t   Time s
Vi   Volume of phase i m3
vi   Velocity vector of phase i m/s
x   Distance m
a, C, G, Y, R   Parameters in turbulence equation
αi   Volume fraction of phase i
ε   Dissipation rate of turbulent kinetic energy m2/s3
ρ   Density of mixture kg/m3
ρi   Density of phase i kg/m3
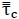  Stress Tensor Pa

REFERENCES

1
P. Kováts, D. Thévenin, and K. Zähringer, "Investigation of mass transfer and hydrodynamics in a model bubble column", Chem. Eng. Technol., vol. 40, no. 8, pp. 1434-1444.
2
J. Behin, and A. Ahmadi, "Mixing parameters for an airlift bioreactor considering constant cross sectional area of riser to downcomer: Effect of sparging gas location", Korean J. Chem. Eng., vol. 27, no. 4, pp. 1226-1232.
3
J. Behin, "Modeling of modified airlift loop reactor with a concentric double-draft tube", Chem. Eng. Res. Des., vol. 88, no. 8, pp. 919-927.
4
J. Behin, and N. Farhadian, "Residence time distribution measurements in a two dimensional rectangular airlift reactor by digital image processing", Exp. Therm. Fluid Sci., vol. 51, pp. 244-250.
5
J. Behin, N. Farhadian, M. Ahmadi, and M. Parvizi, "Ozone assisted electrocoagulation in a rectangular internal-loop airlift reactor: Application to decolorization of acid dye", J. Water Process Eng., vol. 8, pp. 171-178.
6
J. Behin, and N. Farhadian, "Digital image processing technique to investigate the hydrodynamics of an airlift reactor with double downcomer", Chem. Eng. Technol., vol. 38, no. 12, pp. 2207-2216.
7
R.F. Mudde, "Gravity-driven bubbly flows", Annu. Rev. Fluid Mech., vol. 37, no. 1, pp. 393-423.
8
N. Kantarci, F. Borak, and K.O. Ulgen, "Bubble column reactors", Process Biochem., vol. 40, no. 7, pp. 2263-2283.
9
M. Gavrilescu, and R.V. Roman, "Performance of airlift bioreactors in the cultivation of some antibiotic producing microorganisms", Acta Biotechnol., vol. 18, no. 3, pp. 201-229.
10
H.P. Luo, and M.H. Al-Dahhan, "Verification and validation of CFD simulations for local flow dynamics in a draft tube airlift bioreactor", Chem. Eng. Sci., vol. 66, no. 5, pp. 907-923.
11
N. Mahler, S. Tschirren, S. Pflügl, and C. Herwig, "Optimized bioreactor setup for scale-up studies of extreme halophilic cultures", Biochem. Eng. J., vol. 130, pp. 39-46.
12
A. Mota, "Customization of an optical probe device and validation of a signal processing procedure to study gas-liquid-solid flows. Application to a three-phase internal-loop gas-lift Bioreactor", Chem. Eng. Sci., vol. 138, pp. 814-826.
13
L. He, A. B. Chen, Y. Yu, L. Kucera, and Y. Tang, "Optimize Flue Gas Settings to Promote Microalgae Growth in Photobioreactors via Computer Simulations", J. Vis. Exp., vol. 80, .
14
M. Morita, Y. Watanabe, and H. Saiki, "Evaluation of photobioreactor heat balance for predicting changes in culture medium temperature due to light irradiation", Biotechnol. Bioeng., vol. 74, no. 6, pp. 466-475.
15
C. Posten, "Design principles of photo-bioreactors for cultivation of microalgae", Eng. Life Sci., vol. 9, no. 3, pp. 165-177.
16
S. Dhanasekaran, and T. Karunanithi, "Statistical analysis of effects of experimental variables on mass transfer coefficient in a novel hybrid bubble column using Box-Behnken design", Can. J. Chem. Eng., vol. 91, no. 5, pp. 843-854.
17
E. Olmos, N. Mehmood, L. Haj Husein, J.L. Goergen, M. Fick, and S. Delaunay, "Effects of bioreactor hydrodynamics on the physiology of Streptomyces", Bioprocess Biosyst. Eng., vol. 36, no. 3, pp. 259-272.
18
S.K. Jayaraman, and R.R. Rhinehart, "Modeling & control policy optimization of algae growth", Proc. Am. Control Conf., pp. 1995-2000.
19
Z. Chen, Z. Jiang, X. Zhang, and J. Zhang, "Numerical and experimental study on the CO2gas-liquid mass transfer in flat-plate airlift photobioreactor with different baffles", Biochem. Eng. J., vol. 106, pp. 129-138.
20
X. Guo, L. Yao, and Q. Huang, "Aeration and mass transfer optimization in a rectangular airlift loop photobioreactor for the production of microalgae", Bioresour. Technol., vol. 190, pp. 189-195.
21
D.J. Hernández-Melchor, R.O. Cañizares-Villanueva, and J.R. Terán-Toledo, "P. A. López- Pérez, and E. Cristiani-Urbina, “Hydrodynamic and mass transfer characterization of flat-panel airlift photobioreactors for the cultivation of a photosynthetic microbial consortium", Biochem. Eng. J., vol. 128, pp. 141-148.
22
O.N. Manjrekar, Y. Sun, L. He, Y.J. Tang, and M.P. Dudukovic, "Hydrodynamics and mass transfer coefficients in a bubble column photo-bioreactor", Chem. Eng. Sci., vol. 168, pp. 55-66.
23
A. Sadeghizadeh, R. Rahimi, and F. Farhad Dad, "Computational fluid dynamics modeling of carbon dioxide capture from air using biocatalyst in an airlift reactor", Bioresour. Technol., vol. 253, pp. 154-164.
24
S.B. Pawar, "Computational fluid dynamics (CFD) analysis of airlift bioreactor: Effect of draft tube configurations on hydrodynamics, cell suspension, and shear rate", Bioprocess Biosyst. Eng., vol. 41, no. 1, pp. 31-45.
25
A. Amani, E. Jalilnejad, and S.M. Mousavi, "Simulation of phenol biodegradation by Ralstonia eutropha in a packed-bed bioreactor with batch recycle mode using CFD technique", J. Ind. Eng. Chem., vol. 59, pp. 310-319.
26
H. Azargoshasb, S.M. Mousavi, O. Jamialahmadi, S.A. Shojaosadati, and S.B. Mousavi, "Experiments and a three-phase computational fluid dynamics (CFD) simulation coupled with population balance equations of a stirred tank bioreactor for high cell density cultivation", Can. J. Chem. Eng., vol. 94, no. 1, pp. 20-32.
27
F. Calvo, A. Bula, L. Di Mare, and S. Garcia, "CFD simulation of multiphase (liquid–solid–gas) flow in an airlift column photobioreactor", Acta Mech., vol. 228, no. 7, pp. 2413-2427.
28
O.M. Hernández-Calderón, M.D. González-Llanes, E.Y. Rios-Iribe, and S.A. Jiménez-Lam, "M. de. C. Chavez-Parga, and E. M. Escamilla-Silva, “Hydrodynamics and Mass Transfer Simulation in Airlift Bioreactor with Settler using Computational Fluid Dynamics", Int. J. Chem. React. Eng., vol. 15, no. 4, .
29
M. Yang, Y. Wei, X. Zheng, F. Wang, X. Yuan, J. Liu, N. Luo, R. Xu, D. Yu, and Y. Fan, "CFD simulation and optimization of membrane scouring and nitrogen removal for an airlift external circulation membrane bioreactor", Bioresour. Technol., vol. 219, pp. 566-575.
30
T. Zhang, "H. zhen Wu, C. hua Feng, and C. hai Wei, “Modified airlift reactor with a cross-shaped internal and its hydrodynamic simulation by computational fluid dynamic method", Biotechnol. Biotechnol. Equip., vol. 32, no. 1, pp. 194-203.
31
E.K. Nauha, and V. Alopaeus, "Modeling method for combining fluid dynamics and algal growth in a bubble column photobioreactor", Chem. Eng. J., vol. 229, pp. 559-568.
32
A. Packer, Y. Li, T. Andersen, Q. Hu, Y. Kuang, and M. Sommerfeld, "Growth and neutral lipid synthesis in green microalgae: A mathematical model", Bioresour. Technol., vol. 102, no. 1, pp. 111-117.
33
V.K. Pareek, S.J. Cox, M.P. Brungs, B. Young, and A.A. Adesina, "Computational Fluid Dynamic (CFD) simulation of a pilot-scale annular bubble column photocatalytic reactor", Chem. Eng. Sci., vol. 58, no. 3–6, pp. 859-865.
34
C. Montoya-Pachongo, S. Laín-Beatove, P. Torres-Lozada, C.H. Cruz-Vélez, and J.C. Escobar-Rivera, "Efecto de la configuración de entrada de agua en un tanque de compensación aplicando modelación CFD", Ing. Invest., vol. 36, no. 1, pp. 31-40.
35
C. Biscarini, "Computational fluid dynamics modelling of landslide generated water waves", Landslides, vol. 7, no. 2, pp. 117-124.
36
Z. Liu, and B. Li, "Scale-adaptive analysis of Euler-Euler large eddy simulation for laboratory scale dispersed bubbly flows", Chem. Eng. J., vol. 338, no. 3, pp. 465-477.
37
L. Wang, and X.Y. Lu, "Large eddy simulation of stably stratified turbulent open channel flows with low- to high-Prandtl number", Int. J. Heat Mass Transfer, vol. 48, no. 10, pp. 1883-1897.
38
M.T. Dhotre, B. Niceno, B.L. Smith, and M. Simiano, "Large-Eddy Simulation (LES) of the large scale bubble plume", Chem. Eng. Sci., vol. 64, no. 11, pp. 2692-2704.
39
M. Blažej, G.M. Cartland Glover, S.C. Generalis, and J. Markoš, "Gas-liquid simulation of an airlift bubble column reactor", Chem. Eng. Process. Process Intensif., vol. 43, no. 2, pp. 137-144.
40
S.M. Mousavi, A. Jafari, S. Yaghmaei, M. Vossoughi, and I. Turunen, "Experiments and CFD simulation of ferrous biooxidation in a bubble column bioreactor", Comput. Chem. Eng., vol. 32, no. 8, pp. 1681-1688.
41
M.K. Silva, M.A. D’avila, and M. Mori, "Study of the interfacial forces and turbulence models in a bubble column", Comput. Chem. Eng., vol. 44, pp. 34-44.
42
A. Mandal, "Characterization of gas-liquid parameters in a down-flow jet loop bubble column", Braz. J. Chem. Eng., vol. 27, no. 2, pp. 253-264.
43
G. Gris, A.C. Paim, M. Farenzena, and J.O. Trierweiler, "Laboratory apparatus to evaluate microalgae production", Braz. J. Chem. Eng., vol. 30, no. 3, pp. 487-497.
44
C. Santander, P.A. Robles, L.A. Cisternas, and M. Rivas, "Technical-economic feasibility study of the installation of biodiesel from microalgae crops in the Atacama Desert of Chile", Fuel Process. Technol., vol. 125, pp. 267-276.
45
G.C. Buscaglia, F.A. Bombardelli, and M.H. García, "Numerical modeling of large-scale bubble plumes accounting for mass transfer effects", Int. J. Multiph. Flow, vol. 28, no. 11, pp. 1763-1785.
46
V. Ashokkumar, and R. Rengasamy, "Mass culture of Botryococcus braunii Kutz. under open raceway pond for biofuel production", Bioresour. Technol., vol. 104, pp. 394-399.
47
Y. Chisti, "Biodiesel from microalgae", Biotechnol. Adv., vol. 25, no. 3, pp. 294-306.
48
T. Miyahara, Y. Matsuba, and T. Takahashi, "The size of bubbles generated from perforated plates", Int. Chem. Eng., vol. 23, no. 517, .
49
L. Hagesaether, H.A. Jakobsen, and H.F. Svendsen, "A model for turbulent binary breakup of dispersed fluid particles", Chem. Eng. Sci., vol. 57, no. 16, pp. 3251-3267.