All published articles of this journal are available on ScienceDirect.
Experimental Study and Modeling of Solid-liquid Equilibrium for Binary and Ternary Pharmaceutical and Food Systems
Abstract
Background:
The experimental measurement of the solubility of a solute in a given solvent is a difficult task; hence, there is a need for reliable thermodynamic models for its prediction. However, these models require either molecular or group interaction parameters, which are not always available.
Objective:
The objective of the present study is to measure experimentally the solubility of different solutes in solvents selected from pharmaceutical or food fields on the basis that not all the required model interaction parameters are available to use the obtained experimental data for their determination.
Methods:
The experimental study of solid-liquid equilibrium for chosen binary and ternary systems at different temperatures was carried out using differential scanning calorimetry to determine the essential thermophysical properties like melting temperature and enthalpy. The modeling of these phase equilibrium data was performed using thermodynamic models like Random Two Liquids (NRTL) and Universal Functional Activity Coefficient (UNIFAC).
The required NRTL interaction parameters were determined by minimizing a well-defined objective function using the simplex method.
Results:
The solubilities of the solutes in the different considered solvents at different temperatures obtained experimentally provided the required NRTL molecular interaction parameters. Solute solubilities were obtained using NRTL, UNIFAC, and ideal models. The comparisons showed an excellent agreement between the experimental values and the NRTL results, contrary to UNIFAC and ideal case models.
Conclusion:
This study shows the importance of thermodynamic modeling to predict solubility data that may be difficult, time-consuming, and costly to obtain experimentally.
1. INTRODUCTION
The crystallization process may be regarded as a key step in the pharmaceutical industry. It depends upon the solubility of the considered compounds in the used solvents, either organic or inorganic, like supercritical carbon dioxide. However, the experimental measurements of solubility may not be an easy task; hence, there is a need for eveloping reliable predictive correlations and models or improving existing ones. The knowledge of this parameter, i.e., the solubility of a given compound in a pure solvent or mixture of solvents, is essential for the design or calculation of any process involving crystallization. The other major concern is the selection and choice of the most appropriate solvent to use in the crystallization process to develop new pharmaceutical compounds. However, testing experimentally every single potential solvent or mixture of solvents at different operating conditions is an arduous, tedious, and costly task. All these arguments are motivating factors to develop or test solubility in predictive and theoretical calculation ways.
A great number of research works dealing with the solubility of various solutes in different selected solvents are regularly reported in the literature. For instance, Nordström and Rasmussen considered the solubility of salicylic acid in methanol, acetic acid, acetone, water, and ethyl acetate at temperatures in the range of 10 to 50°C [1], and the Differential Scanning Calorimetry (DSC) technique was used to determine the melting properties of salicylic acid. The results showed a correlation between solubility and the Van't Hoff equation [1, 2].
Matsuda et al. used high-performance liquid chromatography (HPLC) to measure the solubility of salicylic acid in the water, methanol, ethanol, ethyl acetate, and in various mixtures of binary solvents, such as methanol + water and ethanol + water. The experimental solubility data were correlated by the two local composition concept models of modified Wilson and Random Two liquids (NRTL) [3].
The determination of the solubility of pharmaceutical compounds in water or organic solvents, mainly alcoholics, has been considered, either experimentally or by modeling in several research works as reported in the literature.
Ninni et al. measured the water activities of binary and ternary mixtures containing polyols like D-sorbitol, D-mannitol, xylitol, meso-erythritol, and glycerol, in the range of 10 to 35°C, using an electronic hygrometer. The concentrations of the mixtures varied according to the solubility limit for each polyol compound. Group contribution-based models like ASOG and UNIFAC were used with interaction parameters from the literature to predict water activity and polyol solubility, but the agreement with experimental values was poor, probably due to the strongly polar hydroxyl groups bounded to consecutive carbon atoms in the polyol molecule. However, improved results were obtained by adjusting the interaction parameters where the UNIFAC-Larsen model achieved an average relative deviation of 0.9% for water activity and solubility data [4].
This literature review showed that different experimental and theoretical methods exist for the determination of solubility data in solvents of different natures. The experimental measurement of such data is a complex task; therefore, using thermodynamic models for its prediction is essential. This has encouraged the present study by considering liquid-solid systems, mainly focusing on compounds with possible pharmaceutical or food applications [4, 5].
Binary and ternary systems were considered to determine experimentally the solute solubility in the solvent and its variation with temperature. As a second part of this work, the modeling of solid-liquid equilibria and the solubility of solutes in the considered various solvents was performed using two different thermodynamic models, such as NRTL and UNIFAC.
2. SOLID-LIQUID EQUILIBRIUM MODELING
Deviations from ideal behavior can be quantified straightforwardly by activity coefficients. Classically, activity coefficients are a common way to link activity to concentration, and for a binary mixture composed of components i = 1, 2, they are related to the molar Gibbs mixing energy ΔGmix, the ideal Gibbs energy ΔGid, and the Gibbs excess energy ΔGE [6] as follows:
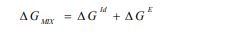 |
(1) |
Therefore, reliable thermodynamic models are needed for the calculation of the activity coefficient, where the well-known ones, namely, UNIFAC and NRTL, are tested in the present work. A brief description is given in the following section.
Generally, the solubility of a solute in a solvent is calculated by means of the following Van’t Hoff relationship [7, 8]:
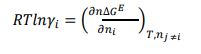 |
(2) |
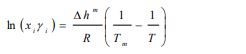 |
(3) |
With xi is the solubility of solute i, γi is the activity coefficient of constituent i, ∆hm is the melting enthalpy, Tm is the melting temperature, T is the temperature, and R is the universal gas constant.
For the ideal case, γi and Van’t Hoff relationship becomes:
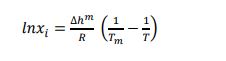 |
(4) |
2.1. Activity Coefficient Model
An activity coefficient is a factor used in thermodynamics to account for deviations from ideal behavior in a mixture of chemical substances [9], and most of the proposed approaches are based on rigorous and robust thermodynamic models considering the non-ideality which prevails in the great majority of systems. They differ in the proposed way to express the excess free Gibbs energy function (GE) in terms of the concentration at a constant temperature for non-ideal liquid mixtures. Some of these models can be regarded as semi-predictive, requiring the knowledge of a number of experimental data.
2.1.1. NRTL (Non-Random Two Liquids) Model
The non-random two-liquid (NRTL) model is frequently applied in chemical engineering to calculate phase equilibria [10]. It is one of the most well-known local composition models for thermodynamic excess functions. These expressions basically are an extension of Wilson’s equations [11, 12], including a non-randomness parameter α [12].
The non-randomness arises from the difference in the interaction energy of the central molecule with the molecules of its own kind and that with molecules of the other kind. It is noted that the assumption made in both the Wilson and the original NRTL equations (with α taken as a constant) that the local compositions around the central molecules i and j are independent of each other leads to an inconsistency in the overall composition of the mixture [11].
The NRTL model involves considering a mixture of n constituents, consisting of n different elementary cells according to the molecule occupying its center [11], thus introducing local molar fractions. It can be generalized to a higher-order two-component mixture and generally gives a good representation of the equilibrium data for all types of mixtures.
According to this model, the activity coefficient for constituent i is expressed as follows:
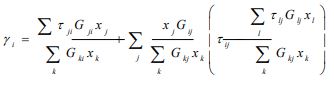 |
(5) |
with
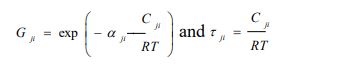 |
(5a) |
with αji the randomness parameter and Cji =gji-gii, gij is the molar free energy due to the interaction between molecules i and j.
2.1.2. NRTL interaction parameters calculation
As mentioned previously, phase equilibrium data are not always available and are not easy to measure for most systems. The prediction of such data is mainly based on the use of reliable thermodynamic models. However, most of these models, like the NRTL, require interaction parameters that are not always available and have to be calculated from experimental values.
Therefore, in the present study, these interaction parameters were determined by minimizing the objective function defined as follows:
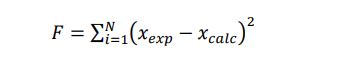 |
(6) |
With xexp and xcalc, the experimental and the calculated solid solute solubilities in the solvent, respectively.
The minimization of the objective function was performed using the simplex method Nelder-Mead version, which is described in detail in the literature [6].
2.2. UNIFAC Model (UNIQUAC Functional –group Activity Coefficient)
The UNIFAC model was proposed by Fredenslund et al., where a molecule was considered a set of functional groups. Binary or ternary systems are then regarded as groups rather than molecular mixtures [2]. According to this model, the activity coefficient was supposed to be the sum of two contributions: a combinatorial part, essentially due to the difference in the size and shape of the molecule in the mixture and a residual part related to the interaction energy [12].
The link between the structural groups and the main groups was defined by Fredenslund et al. mainly based on experiments [12].
According to the UNIFAC model, the activity coefficient is defined as follows [12]:
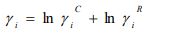 |
(7) |
with:
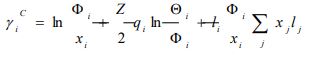 |
(7a) |
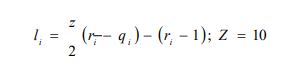 |
(7b) |
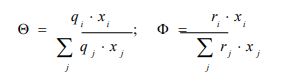 |
(7c) |
xi represents the molar fraction of constituent i, and the summations are all over the constituents; and are the surface area and volume fractions, respectively, ri and qi are the molecular volume and surface area, respectively, and can be calculated as follows:
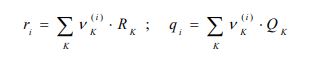 |
(7d) |
where is the number of type k groups in molecule I; Rk and Qk are the group volume and surface parameters which are readily available in standard table or can be calculated from the following relationships:
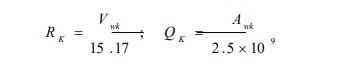 |
(7e) |
With and are the volume and surface area of group k, respectively.
The residual term is given as follows:
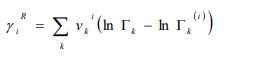 |
(7f) |
Where and are the residual activity coefficients of group k in the mixture and pure liquid i, respectively. The residual activity coefficient of group k is then expressed as follows:
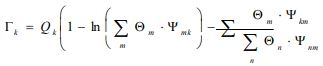 |
(7g) |
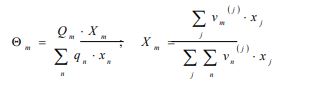 |
(7h) |
With and are the group surface and molar fractions, respectively, in the solution mixture.
The interaction parameter between groups m and n is then calculated from the following:
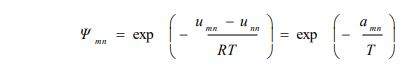 |
(8) |
is the Boltzmann factor corresponding to the binary system.
To illustrate these applications, the prediction of the solubility of a pharmaceutical compound in selected solvents was considered in the present work, using the UNIFAC and the NRTL models for the activity coefficient calculations, and the results are shown in the following section.
3. MATERIALS AND METHODS
Generally, the techniques of solubility determination of a solute in a solvent are relatively simple. However, they require great care due to the difficulty of reaching a complete state of equilibrium of the solid in the liquid solution. Therefore, it is necessary to maintain intimate and prolonged contact between both phases.
The current experimental study concerns measurements of liquid-solid phase equilibrium for binary and ternary systems, using the Differential Scanning Calorimetry technique (DSC92 of SETARAM) for the determination of key properties like melting temperature and enthalpy.
3.1. Chemicals
The solutes, such as salicylic acid used in the present study, were provided by LABOSI (France), Vanillin and D-Mannitol by ALDRICH (Sigma-Aldrich .ca), D-Sorbitol by VWR- BDH PROLABO, Ethanol by PANREAC Quimica SA (PRS Spain), and Formamide by BIOCHEM CH Emopharma. Water was bi-distilled locally using a GFL 2001/4 distillation unit.
3.2. Experimental Procedure
Solutions were prepared in a jacketed glass beaker using tap water to keep a constant temperature. The solutions were magnetically agitated at a constant speed of 200 rpm for 30 minutes to ensure good mixing of the dissolved solids and liquid solvent. The solutions were then left at rest and gently decanted, allowing sufficient time to solidify. Solid compounds were then encapsulated in standard aluminium sealed pans with a pierced cover lid for DSC analyses. The reference pan used for each experiment was empty and identical to the one used on the measuring side. Temperature scans were performed over the temperature range of 0 to 200°C with an average heating rate q = 1°C min-1 [5]. The temperature calibration was made using three reference standards, indium, zinc, and lead. The obtained deviations were negligible [5].
3.2.1. Calibration
For the present study, a SETARAM DSC92 calorimeter was used and a priori calibrated with indium. The samples were analyzed over a temperature range from 0 to 180ºC, with a heating rate of 1ºC / min. Three successive passages were performed for each sample. For this, three tests were carried out, with three samples of equivalent mass equal to 23.4 mg. The results are shown in the following Table 1.
| Run | Enthalpy of Melting (J/g) | Melting Temperature (°C) |
|---|---|---|
| 1 | 28.25 | 158.66 |
| 2 | 28.35 | 158.88 |
| 3 | 28.20 | 158.85 |
The onset temperature for melting was around 156.6 and 157.6°C [5] for a melting enthalpy between -26.8 and -30.2 J/g [5]. Therefore, the results are given as mean values throughout this study.
The obtained experimental results for the different considered solutes using the DSC technique are shown in the following Table 2.
4. RESULTS AND DISCUSSION
4.1. Binary Systems
4.1.1. Experimental Equilibrium Data
The obtained experimental results for the three considered binaries: D-Mannitol-Water, D-Mannitol-Trehalose, and D-Mannitol-Lactose, are shown in Table 3.
| System | T [K] | x(1) Exp |
| D-Mannitol(1) – Water (2) | 368.10 | 0.101 |
| 372.27 | 0.240 | |
| 409.38 | 0.400 | |
| 427.21 | 0.560 | |
| 438.64 | 0.810 | |
| 438.98 | 1.000 | |
| System | T [K] | x(1) Exp |
| D-Mannitol (1) – Trehalose (2) | 476.15 | 0.000 |
| 472.15 | 0.090 | |
| 469.15 | 0.173 | |
| 465.15 | 0.249 | |
| 464.15 | 0.320 | |
| 428.15 | 0.738 | |
| 430.15 | 0.814 | |
| 436.15 | 0.944 | |
| 438.98 | 1.000 | |
| D-Mannitol (1) - Lactose (2) | 481.35 | 0.004 |
| 481.02 | 0.089 | |
| 478.97 | 0.173 | |
| 458.48 | / | |
| 446.35 | / | |
| 432.58 | 0.7367 | |
| 433.56 | 0.8839 | |
| 436.27 | 0.9459 |
These experimentally measured data were used to determine the required interaction parameters for the NRTL model, as shown in the next section.
4.1.2. Interaction Parameters
The minimization of the objective function defined in Equation 6 for the three considered binaries led to the following NRTL binary interaction parameters.
These parameters were used to calculate the solubility of D-Mannitol in water, trehalose, and lactose with NRTL as the activity coefficient model. From Table 4, it can be seen that these parameters have shown a certain dependence on temperature, where different interaction parameters were obtained in two different temperature ranges.
| System | A12 | A21 |
|---|---|---|
| D-Mannitol (1) - Water (2) T ϵ [375, 409 K] T ϵ [410, 440 K] |
-243.450 314.250 |
278.470 - 275.440 |
| D-Mannitol(1) -Trehalose (2) | -201.771 | 225.537 |
| D-Mannitol (1) - Lactose (2) | -169.499 | 186.570 |
For the UNIFAC model, the involved functional groups are shown in the following Table 5.
The UNIFAC interaction parameters and the volume and surface parameters (Equation 5) are obtained from previously reported table [12].
The calculated solubilities of D-Mannitol in water, trehalose, and lactose using the three models (UNIFAC, NRTL, and Ideal case), as well as their comparison with experimentally measured values, are shown in the following Fig. (1a-c).
For the UNIFAC and the IDEAL models, the solubilities of D-mannitol can be calculated at any temperature because the required data consisting of group interaction parameters and thermophysical properties, respectively, are always available. However, this is not possible for the NRTL model, which requires molecular and not group interaction parameters, which are not available and have to be calculated from experimental data. The solubilities of D-Mannitol in water at the different experimental temperatures are shown in Fig. (1a) and also in the following Table 6.
| T (K) | Experimental | UNIFAC | IDEAL | NRTL |
|---|---|---|---|---|
| X(1) | X(1) | X(1) | X(1) | |
| 376.10 | 0.1010 | 0.1548 | 0.1225 | 0.1072 |
| 378.27 | 0.2400 | 0.1681 | 0.1346 | 0.2527 |
| 409.38 | 0.4000 | 0.4150 | 0.4100 | 0.3808 |
| 427.21 | 0.5610 | 0.6500 | 0.7050 | 0.5610 |
| 438.64 | 0.8110 | 0.9100 | 0.9460 | 0.8110 |
| 438.98 | 1.0000 | 0.9490 | 0.9670 | 1.0000 |
Fig. (1a-c) show that the results obtained using the NRTL model for the solubility of D-mannitol in the three solvents, water, trehalose, and lactose, were in a very good agreement with the experimental values, contrary to those obtained using UNIFAC and the IDEAL models. This confirms the reliability of the optimization technique based on the Simplex method used for the determination of NRTL molecular interaction parameters that are available for further calculations of solubility data.
For the D-mannitol-water system, it is found that the solubility increases with the increase in temperature. D-mannitol is a polyol having several alcohol functions. Therefore, it showed good solubility in water, and the modeling by assuming an ideal case gave reasonable results. This can be explained by the similarity between the interactions of D–mannitol and water molecules; both are characterized by hydrogen bonding. Moreover, for this solute, the results obtained by UNIFAC and the ideal case were quite close.
The other two binary systems, D-mannitol-trehalose and D-mannitol-lactose, exhibited different solubilities than those reported for D-mannitol-water. They both showed their respective eutectic points, which are generally difficult to determine experimentally and therefore are very often predicted using thermodynamic models [13]. Table 7 shows the results for the two binaries as follows:
The two branches of the solid-liquid equilibria must finish at the eutectic points. Fig. (1b and c) show that for the NRTL model, both the experimental data and the predicted results, the temperatures did not cross the corresponding horizontal dashed lines going through the respective eutectic points. However, the predictions obtained by the UNIFAC and the IDEAL models showed that two branches went below the dashed lines, hence below the respective eutectic points. This confirmed the reliability of NRTL and the weakness of the two other models (Ideal and UNIFAC).
| Method | Eutectic Point (K) | Solubility |
|---|---|---|
| D-Mannitol (1) Trehalose (2) | ||
| Experimental | 428.15 | 0.738 |
| UNIFAC | 430.57 | 0.753 |
| NRTL | 428.10 | 0.738 |
| Ideal | 430.20 | 0.751 |
| D-Mannitol (1) -Lactose (2) | ||
| Experimental | 432.90 | 0.743 |
| UNIFAC | 426.51 | 0.710 |
| NRTL | 432.25 | 0.740 |
| Ideal | 431.22 | 0.7527 |
Moreover, the results obtained using NRTL were very close to the experimental values for both systems (D-Mannitol –Trehalose and D-Mannitol-Lactose), comparatively to the other two models (UNIFAC and the ideal case model). These results confirmed the fact that a group contribution-based model remains approximately contrary to a molecular-based model.
4.2. Ternary Systems
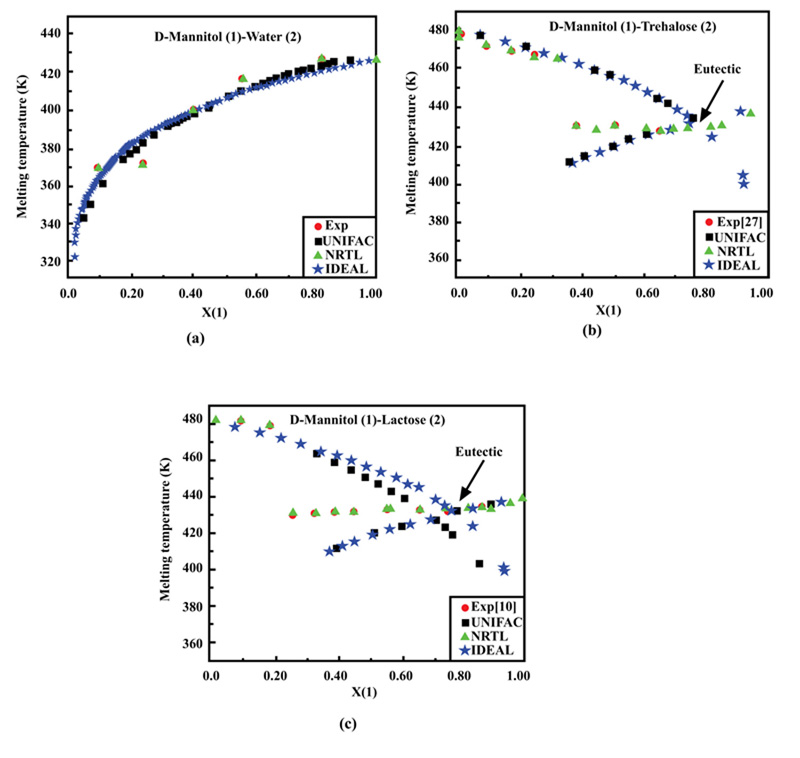
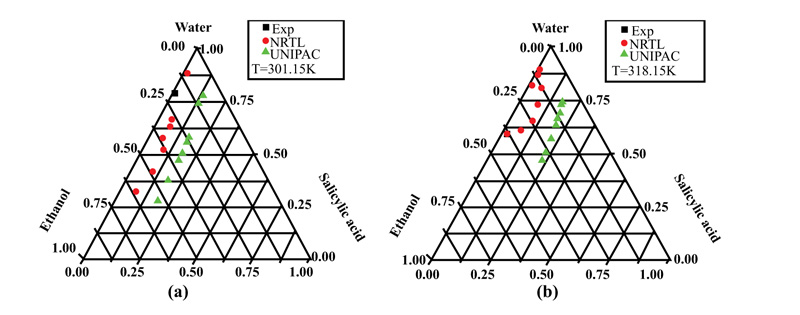
Ternary systems of a solute in a binary mixture of solvents were selected for solubility calculations using the UNIFAC and NRTL models. Four solutes, salicylic acid, vanillin, D-sorbitol, and D-mannitol, were considered in mixtures of ethanol or formamide with water at different fixed temperatures.
The minimization of the objective function expressed by Equation 6 led to the NRTL interaction parameters,as shown in Table 8.
These parameters were used to predict the solid-liquid equilibria, and the obtained results concerning these systems are shown in Figs. (2-5).
The results for all considered ternary systems at different temperatures confirmed the reliability of the NRTL model to predict different solubilities, whereas the UNIFAC model led to important deviations for certain conditions, confirming the limitations of the group contribution concept.
Some interesting results can also be observed from the above Figures. For instance, in Fig. (2a and b), the different data points representing ternary solutions are close to the water-ethanol side and far from the apex representing salicylic acid. This confirms that this solute is generally slightly soluble in water and ethanol.
Fig. (3a and b) show the behavior of vanillin in the mixture of solvents (Water + Ethanol) at two different temperatures of 315.15 and 319 K. The molecule of this solute represents an important class, where three functional groups (hydroxyl, aldehyde, and methoxy) are present on the aromatic ring. From these figures, it can be seen that vanillin was soluble in the presence of ethanol. Regarding the influence of temperature, the solubility was greater at 319 than at 315.15 K
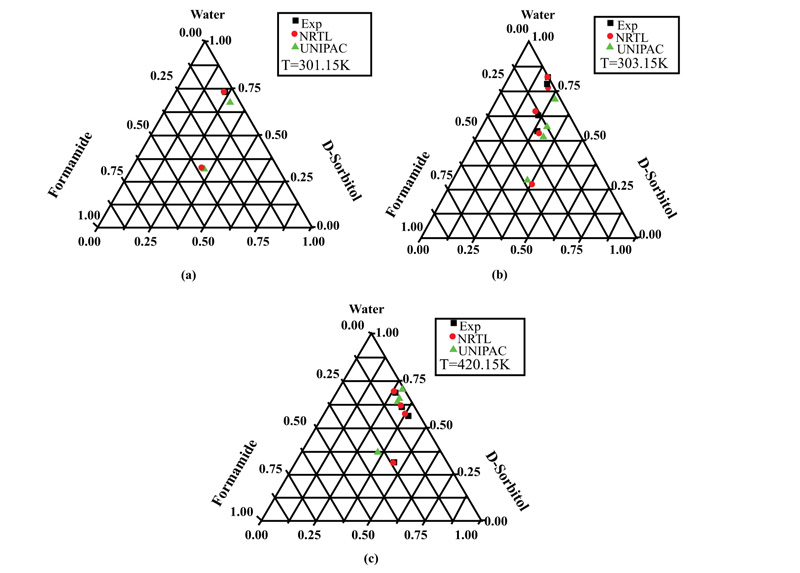
For the D-Sorbitol-Water-Formamide system, the results are shown in Fig. (4a-c) at temperatures of 301.15, 303.15, and 420.15K, respectively. Moreover, it can be seen that the results obtained using NRTL were very close to the experimental values, independently of temperature. However, the results showed that the solubility of D-sorbitol in the solvent mixture increased with increasing temperature.
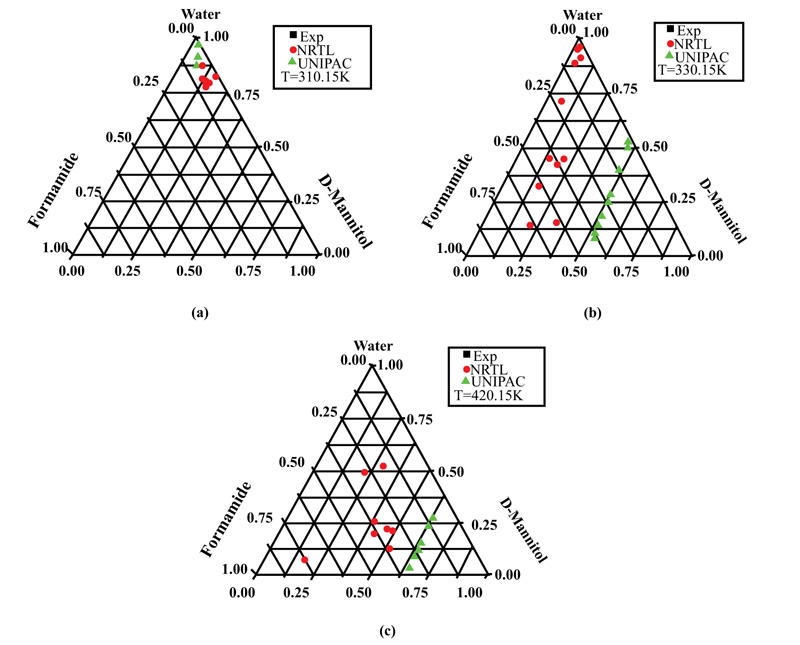
Fig. (5a-c) show the results for the D-Mannitol-Water-Formamide system at 310.15, 320.15, and 420.15K, respectively. It can be seen that at the lowest temperature (310.15K), water was the main constituent of the ternary solution, the D-Mannitol solubility values were around 0.125, and the fractions were low, around 6%. As the temperature increased to 320.15 or 420.15 K, D-mannitol solubility values increased in the ternary solutions but were spread out over the triangular plane.
This can be explained by the fact that the solubility of D-mannitol in water and formamide is low compared to that of D-sorbitol. Some results, like those in Fig. (4a), show the appearance of a solid phase in equilibrium with pure formamide.
This result confirms the reliability of the optimization technique based on the simplex method, which made it possible to determine the molecular interaction parameters, thus becoming available for calculating the equilibrium data.
| Systems | T[K] | Interaction Parameters | |||||
|---|---|---|---|---|---|---|---|
| A12 | A13 | A21 | A23 | A31 | A32 | ||
| Water (1)-Ethanol(2)- Salicylic acid (3) |
300.15 | -1.083 | 4.090 | 0.000 | 3.792 | 18.803 | 0.000 |
| 318.15 | 1.268E-007 | 6.789 | 0.000 | 51.852 | 96.801 | 0.000 | |
| Water (1)-Ethanol(2)-Vanillin(3) | 315.15 | 1.267E-007 | 6.789 | 0.000 | 51.852 | 96.801 | 0.000 |
| 319.15 | -7.749E-007 | 2.866 | 0.000 | -38.554 | -49.863 | 0.000 | |
| Water(1)- Formamide(2)- D-Sorbitol (3) |
301.15 | 8.634 | 3.118 | -1.004 | -3.703 | -1.859 | 5.433 |
| 303.15 | 96.809 | 152.257 | -91.024 | -237.995 | -138.447 | 289.503 | |
| 308.25 | 97.774 | 121.932 | -92.032 | 87.625 | -47.900 | 9525.010 | |
| Water (1)- Formamide (2) D-Mannitol (3) |
310.15 | 1.239 | -5.538 | 0.000 | -793.403 | -876.119 | 0.000 |
| 330.15 | -2.5E-006 | -0.287 | 0.000 | -4.689 | 3.620 | 0.000 | |
| 420.10 | 3.260 | 2.864 | 0.000 | 1.626 | 4.988 | 0.000 | |
CONCLUSION
The fundamental objective of this work was to consider the determination of the solubility of different solutes in various solvents related to systems of pharmaceutical and agro-food interest. The choice of solvent is also a very difficult task and is not always obvious. Generally, it would require great, long, and expensive experimental work, in particular during the development of a new active ingredient, where the quantity available in the active molecules is limited.
To circumvent these difficulties and solve this problem, reliable predictive methods for the determination of solubility in different solvents are needed. Therefore, research work should focus on the improvement of existing thermodynamic models and/or the development of new ones.
The obtained results clearly showed the great reliability of NRTL compared to UNIFAC. This outlined the reliability of molecular models over the group contribution ones when used for the representation of liquid-solid equilibria. However, the major drawback of the molecular thermodynamic models is the non-availability of the required molecular interaction parameters, which have to be calculated from experimentally measured data.
Generally, differential scanning calorimetry is very reliable for the determination of relevant thermophysical properties for solubility calculations, like the melting temperature and enthalpy. This was confirmed in the present study, where the obtained results were very accurate in comparison with the literature and permitted the calculation of solubility and molecular interaction parameters for the exploitation of models like NRTL.
Finally, the results can be regarded as encouraging for the study of specific systems belonging to the pharmaceutical and food fields, where crystallization depends upon the solubility of the solute in the used solvent and may be frequently involved in the corresponding processes.
LIST OF ABBREVIATIONS
| UNIFAC | = Universal Functional Activity Coefficient |
| NRTL | = Random Two Liquids |
CONSENT FOR PUBLICATION
Not applicable.
AVAILABILITY OF DATA AND MATERIALS
The data supporting the findings of the article is available within the article.
FUNDING
None.
CONFLICT OF INTEREST
Dr. Abdeslam-Hassen Meniai is on the editorial advisory board of The Open Chemical Engineering Journal.
ACKNOWLEDGEMENTS
Declared none.


