Prediction of Filtration Properties of Portland Cement Concrete Based on the Results of Calibration of the Basic Hydration Simulation

All published articles of this journal are available on ScienceDirect.

RESEARCH ARTICLE

Prediction of Filtration Properties of Portland Cement Concrete Based on the Results of Calibration of the Basic Hydration Simulation

Ekaterina A. Tyupina1 , * Open Modal iD Pavel P. Kozlov1 iD Kirill A. Boldyrev2 iD Victoria V. Krupskaya3 iD
Authors Info & Affiliations
The Open Chemical Engineering Journal • 27 Mar 2025 • RESEARCH ARTICLE • DOI: 10.2174/0118741231367631250313070739
Previous Article

Abstract

Introduction

Ordinary Portland cement-based materials are considered in many concepts of geological isolation of Radioactive Waste (RW) for the design of Engineered Safety Barriers (ESB). The safety functions of cement-based EBS consist of limiting the access of groundwater to the near zone of the Geological Disposal Facility (GDF) of RW and reducing the rate of migration of radionuclides due to diffusion. These factors can be described by the hydraulic conductivity and effective diffusion coefficient values, mainly determined by the porosity of the barrier material.

Methods

The article presents experimental data used to calibrate the basic hydration simulation of Ordinary Portland Cement (OPC) concrete considered as a potential material for an engineered barrier in the GDF in the “Yeniseisky” site of the Nizhnekansky crystalline rock massif in the Krasnoyarsk region based on the simulation results using PhreeqC 3.7.3 software.

Results

As the result of the current work phase composition of the initial binder and concrete, as well as the chemical composition of water added to the concrete mixture, were established. The obtained data were used for the parameterization of the basic simulation of OPC concrete mixture hydration.

Conclusion

OPC concrete porosity, hydraulic conductivity, and pH of the pore solution were calculated. Obtained values wereconsistent with the analytical data collected during the experiments, and the values of the effective diffusion coefficients of the radionuclides that pose the greatest threat to the biosphere and are expected to be isolated in the GDF were predicted.

Keywords: Concrete, Ordinary portland cement, Hydration, Hydraulic conductivity, Effective diffusion coefficient, Radionuclide migration, Simulation, Radioactive waste.

1. INTRODUCTION

RW class 1 and 2 are High-Level Waste (HLW) with high heat release (more than 100 W/m3) and low-heat-release (less than 100 W/m3) or Intermediate-Level Waste (ILW) containing long-lived radionuclides, respectively [1]. In accordance with the requirements of Federal Law No. 190-FL and Federal Norms and Rules NP-055-14 [2, 3], such RW must be isolated in a GDF at a distance of more than 100 m below the ground surface. For this purpose, the Russian Federation plans to construct a GDF at the “Yeniseisky” subsoil area in the Krasnoyarsk region, located at a depth of about 500 meters in a crystalline rock massif [4-6]. The list of radionuclides potentially posing the greatest threat to the biosphere, which are part of the RW class 1 and 2 considered for isolation in the GDF, includes iodine-129, technetium-99, cesium-135, americium-243, plutonium-239, uranium-238, and selenium-79 [7, 8]. Also, when disposing off spent graphite from RBMK-1000 reactors with possible isolation in the GDF, the possibility of radionuclides such as chlorine-36 and carbon-14 getting into groundwater should be taken into account [9-15].

Safety during operation of the GDF is ensured by creating an Engineered Barrier System (EBS) – a complex of several independent levels of environmental protection from the ingress of radionuclides [5, 7]. Cement-based materials are one of the universal options that have found their application in the creation of EBS in the worldwide practice of long-term disposal of RW in deep geological formations, as the following ESB components [16-22]: matrices for ILW localization, lining and engineered plugs/seals of tunnels/boreholes made of concrete in the host rock. Based on the current proposed EBS layout in the GDF at the “Yeniseisky” subsoil area, it is planned to use concrete for the creation of borehole lining in the host rock with vertical placement of RW containers [5].

One of the safety functions of concrete as an ESB material is physical localization, i.e., limiting the access of significant volumes of groundwater with RW due to low values of the filtration properties (hydraulic conductivity) of the host rock and EBS components [23].

Due to the relatively low hydraulic conductivity of concrete (< 8×10-7 m/day), the rate of migration of radionuclides during failure of RW containers will be determined mainly by diffusion mass transfer, similar to clay barrier materials [24-26].

The Swedish concept of RW disposal in deep geological formations KBS-3 considers the following safety functions of cement-based ESB [27]:

• Fixation of the bentonite buffer layer inside the tunnel for a period of time corresponding to the saturation of the bentonite with groundwater to prevent it from leaking outside the tunnel due to swelling.

• Elimination of advection mass transfer of bentonite buffer, which leads to a decrease in the dry density and, consequently, a decrease in swelling pressure

• Creating a chemical environment that prevents the bentonite buffer's key properties from being negatively impacted (creating a pH of the media during filtration of groundwater through the ESB material that is several values lower than when using conventional OPC concrete) [28].

Thus, an important parameter of concrete when used in GDF as ESB in contact with a buffer layer of compacted bentonite is the pH of the pore solution. pH value determines the potential negative impact on the insulating properties of the clay material when exposed to groundwater from the host rock massif [29-32].

According to the data in the paper,, the characteristics of the filtration properties of ESB in the GDF include effective diffusion coefficients of radionuclides (De) and hydraulic conductivity (k) [33]. The determination and prediction of De and k is part of a series of studies aimed at the reliable isolation of the most dangerous classes of radioactive waste in the “Yeniseisky” subsoil area of the Nizhnekansky massif of crystalline rocks.

Prediction of the hydraulic conductivity values depending on the microstructure of the material is the subject of many studies. One of the known methods for estimating the values of hydraulic conductivity as a function of porosity is the use of the Kozeny-Carman equation [34, 35]. In the report, based on this equation, the hydraulic conductivity was predicted relative to the characteristics obtained for reference concrete using the following equation (1) [36]:

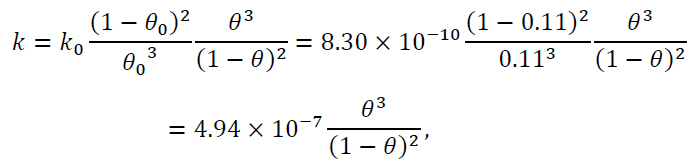(1)

where k is the predicted hydraulic conductivity, m/s; k0 is the hydraulic conductivity obtained for the reference material, m/s, θ is the porosity obtained to predict the filtration coefficient of the concrete under study, and θ0 is the porosity of the reference material.

A number of papers are devoted to predicting the values of the effective diffusion coefficient of chloride ions in concrete as a characteristic of the long-term resistance of reinforced concrete structures to the impact of seawater [37, 38]. The application of this equation in a previous study to predict the diffusion coefficients is limited to chloride ions only [37]. However, for the equation obtained in the article [38], it is possible to use it to estimate the De of other elements, but this fact must be experimentally confirmed. In various reports [36, 39], the diffusion coefficients were calculated based on the obtained data on the porosity of various concretes as a result of simulation of the hydration of the concrete mixture, as well as the host rock massif to assess the long-term safety of geological isolation of RW using the following equation (2) and reference values from Table 1:

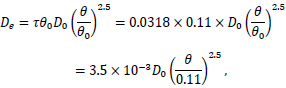(2)

where De is the effective diffusion coefficient, m2/s, τ is the tortuosity of the pore space of the reference material, and D0 is the diffusion coefficient in free water m2/s [39].

Therefore, the aim of this work is to create a basic simulation of Portland cement concrete hydration to predict the values of the hydraulic conductivity of groundwater and the effective diffusion coefficients of radionuclides as characteristics of filtration properties for a long period of operation.

2. MATERIALS AND METHODS

2.1. Materials

The composition of concrete for the study was selected based on the data in the report of the Swedish Nuclear Fuel and Waste Management Company SKB (Svensk Kärnbränslehantering Aktiebolag) [40]. The binder used in the study was ordinary Portland cement grade CEM I 52.5N (GOST 31108-2003). Quartz sand with a fraction of > 200 μm served as a filler for the concrete mixture. The Water-Cement ratio (W/C) was 0.67. The concrete samples were cured in a desiccator for 28 days at a relative humidity of ~ 95%, according to GOST 10180–2012 [41].

2.2. Methods

X-Ray phase Diffraction (XRD) patterns of the initial cement binder and concrete based on it were obtained using a Rigaku Ultima-IV (Cu-Kα) diffractometer in the range of 3°–65° 2θ with a step of 0.02° and a scanning speed of 3° 2θ/min. The phase composition was analyzed from the obtained diffraction patterns using MDI Jade 6.5 software and the ICDD PDF-2 database. The quantitative phase composition of Portland cement was analyzed using the Rietveld method in Profex Software for BGMN 5.2 with the COD and ICSD databases [42, 43].

The chemical composition of the water added to concrete mixture was determined using a ThermoScientific iCAP-Qc Inductively Coupled Plasma Mass Spectrometer (ICP-MS).

The density of concrete was measured by weighing samples on an Ohaus PR224 analytical balance and calculating the volume based on their geometric dimensions.

Table 1.
Recommended values of diffusion coefficients in free water [39].
Element/specie D 0 × 10 9 , m 2 /s
НТО 2.4
C/CO3 1.2
Cl 2
I 0.83
Cs 2.1
Sr 0.79
Other 1.0
Fig. (1).

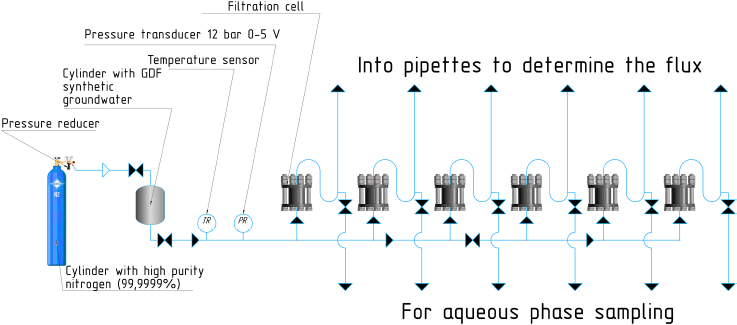
The schematic image of the laboratory setup.

The pore volume was determined on a Quadrasorb SI/Kr setup by adsorption of high-purity nitrogen (99.9999%) and calculations using the Barrett-Joyner-Halenda (BJH) model according to the recommendations in a previous study [44] The isotherms obtained were analyzed using QuadraWin software. . Porosity was calculated as the product of the pore volume and the sample density. Degassing of the samples before analysis was carried out at 105°C on a FloVac Degasser setup until the vacuum required for measurements was achieved.

The pH of the concrete pore solution was determined using the Cold Water Extraction (CWE) method, described in detail in another study [45], and by direct measurement of the supernatant obtained by centrifuging the concrete mixture that had hydrated for 2 hours (based on the method presented in [46]) using an Anion-4100 laboratory pH meter and an ESLK-01.7 combined electrode with a glass electrolytic key.

The hydration simulation was performed using the PhreeqC 3.7.3 [47] calculation code and the CEMDATA18.1-16-01-2019-phaseVol.dat and llnl.dat databases. The following ratios were used to create the simulation: hydraulic binder - 1000 g, filler - 1663 g, and water - 667 g. Quartz sand was specified during the simulation parameterization as a material inert to dissolution with a solubility constant Ksp = 1 10-30.

The schematic image of the setup for determining the filtration coefficient of Portland cement concrete is shown in Fig. (1). The operating principle of the setup consists of feeding synthetic groundwater under a pressure of 1 MPa, selected on the basis of data from the underground research laboratory Grimsel Test Site (Switzerland) [19], through filtration cells containing cylindrical concrete samples with a diameter of 47 mm and a height of 31 mm. The pressure and temperature in the system were recorded using an analog pressure transducer and a digital temperature sensor. The value of the Portland cement concrete hydraulic conductivity was established earlier in a previous study [48].

2.3. Sample Size and Statistical Justification

The sample size in this study was determined based on the following considerations:

2.3.1. Representativeness of the Material

The concrete samples were prepared using a standardized mix design, as specified in the report of the Swedish Nuclear Fuel and Waste Management Company (SKB) [ 40 ]. This mix design is representative of the concrete intended for use in engineered barriers for radioactive waste isolation. Given the homogeneity of the concrete mixture and the controlled conditions under which the samples were prepared, a smaller number of samples was deemed sufficient to capture the material's properties.

2.3.2. Experimental Constraints

The study involved extensive experimental procedures, including X-Ray Diffraction (XRD), Inductively Coupled Plasma Mass Spectrometry (ICP-MS), and pore size distribution analysis using nitrogen adsorption. These methods require significant time and resources, which limits the number of samples that could be processed. However, the samples were carefully selected to ensure they were representative of the material's behavior under the studied conditions.

2.3.3. Previous Studies and Standards

The sample size was also informed by previous studies on cement hydration and filtration properties, where similar sample sizes were used to achieve reliable results [ 36,39]. Additionally, the sample preparation and testing procedures followed established standards (e.g., GOST 10180-2012 [41]), which provide guidelines for the number of samples required to obtain statistically valid results.

To ensure the reliability and statistical significance of the results, the following steps were taken:

2.3.4. Replication of Measurements

Each experimental measurement (e.g., XRD, ICP-MS, pore size distribution) was performed in triplicate to account for variability and ensure reproducibility. The average values and standard deviations were calculated to assess the consistency of the results.

2.3.5. Error Analysis

The relative error between experimental and simulated results was calculated for key parameters such as porosity, pH, and hydraulic conductivity. The small relative errors (ranging from 0.32% to 13.09%) indicate that the sample size was adequate to achieve reliable results.

2.3.6. Comparison with Literature Data

The results obtained in this study were compared with literature data [ 36,39,49], and the close agreement further supports the adequacy of the sample size. The predicted effective diffusion coefficients of radionuclides were consistent with previously reported values, indicating that the sample size was sufficient to capture the material's behavior.

2.3.7. Power Analysis

Although a formal power analysis was not conducted due to the exploratory nature of the study, the consistency of the results across multiple measurements and the agreement with literature data suggest that the sample size was appropriate for the objectives of this study.

In conclusion, the sample size was selected based on the representativeness of the material, experimental constraints, and adherence to established standards. The replication of measurements, error analysis, and comparison with literature data provide statistical justification for the adequacy of the sample size in achieving reliable and statistically significant results.

3. RESULTS AND DISCUSSION

As a result of the XRD, an X-ray diffraction pattern of the initial cement binder was obtained (Fig. 2). The present phases were identified based on the detected reflexes, and the quantitative composition was calculated, presented in Table 2.

For further calibration and parameterization of the simulation, an analysis was made of the qualitative composition of the concrete samples obtained on the basis of the initial binder. The X-ray diffraction pattern of the obtained concrete sample is presented in Fig. (3), as well as the phase composition, presented in Table 3.

The pore size distributions calculated from the desorption isotherm using the BJH model, according to a previous study [44] are shown in Fig. (4).

The obtained results demonstrated that the pore size of Portland cement concrete is 4 nm. Also, the analysis of the integral pore size distribution curve shows that the pore volume of the Portland cement concrete sample is 0.078 cm3/g.

The chemical composition obtained as a result of ICP-MS and the pre-measured characteristics of distilled water used for mixing the binder-filler mixture, used for parameterization of the basic simulation of Portland cement concrete hydration, are presented in Table 4.

Fig. (2).

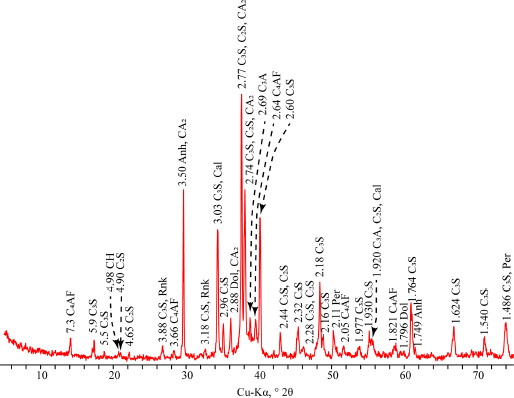
X-ray diffraction pattern of a sample of cement grade CEM I 52.5N: C4AF – ferrite, C3S – alite; C2S – belite, C3A – tricalcium aluminate, CA2 – grossite, CH – portlandite; Rnk – rankinite, Cal – calcite, Per – periclase, Dol – dolomite, Anh – anhydrite..

Table 2.
The quantitative phase composition of cement binder grade CEM I 52.5N.
Phase Chemical Formula Content, % Wt.
Alite (С3S) 3CaO·SiO2 55.5
Belite (C2S) 2CaO·SiO2 14.1
Anhydrite (Anh) CaSO4 2.4
Calcite (Cal) CaCO3 4.0
Portlandite (CН) Ca(OH)2 0.8
Dolomite (Dol) CaMg(CO3)2 4.4
Tricalcium aluminate (С3А) 3CaO·Al2O3 6.3
Ferrite (C4AF) 4CaO·Al2O3·Fe2O3 9.4
Grossite (СА2) 2CaO·2Al2O3 1.1
Rankinite (Rnk) Ca3Si2O7 1.4
Periclase (Per) MgO 0.6
Fig. (3).

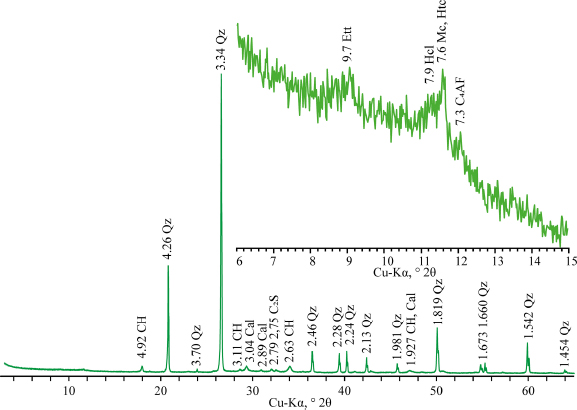
X-ray diffraction pattern of a sample of portland cement concrete. CH – portlandite, Qz – quartz, Cal – calcite, C2S – belite, C4AF – ferrite, Ett – ettringite, Hcl – hydrocalumite (“Friedel’s salt”), Htc – hydrotalcite, Mc – calcium monocarbonate.

Table 3.
Phase composition of the analyzed concrete sample.
Phase Chemical Formula
Belite (C2S) 2CaO·SiO2
Ettringite (Ett) Ca6Al2(SO4)3(OH)12·26H2O
Calcite (Cal) CaCO3
Portlandite (CН) Ca(OH)2
Ferrite (C4AF) 4CaO·Al2O3·Fe2O3
Quartz (Qz) SiO2
Hydrocalumite (Hcl) Ca8Al4(OH)24(CO3)Cl2·9,6H2O
Hydrotalcite (Htc) Mg2Al(OH)6(CO3)0,5·1,5H2O
Calcium monocarbonate (Мс) Ca4Al2(OH)12CO3·5H2O

Based on the results of the quantitative phase composition of the initial cement and the qualitative phase composition of the Portland cement concrete, the input data for the basic simulation of Portland cement concrete hydration were formed and are presented in Table 5. The C-S-H phase was not detected by the X-ray phase analysis of the obtained Portland cement concrete. The theoretical assumption on the type of the C-S-H phase was made as a result of preliminary calibration of the simulation by the maximum value of the Saturation Index (SI), which is a characteristic of the precipitation of the phase available in the databases used for the calculation. Also, during the calibration of the simulation, excess iron content in the equilibrium liquid phase was established, for which iron hydroxide was used as a secondary phase in the input parameters, the thermodynamic and dissolution equations of which were taken from the llnl.dat database.

Thus, the parameterization of the basic simulation of hydration of Portland cement concrete was performed. Further calibration was performed based on the results of determining the density of concrete, the pH of the pore solution, and the filtration coefficient obtained during the experiments. A summary table containing a comparison of experimental data and calculations based on the simulation results is presented in Table 6.

Based on the combination of experimental and calculated data, it was found that the simulation of hydration of Portland cement concrete showed values of porosity, pH of the pore solution, and filtration coefficients close to the experimental ones, which confirms its correctness for predicting the initial characteristics. Minor differences from the experimental data are explained by the lack of consideration of the hydration kinetics of the original cement, which is planned to be taken into account when optimizing the simulation.

The results of calculating the predicted effective diffusion coefficients of potentially hazardous radionuclides intended for isolation in the GDF at the “Yeniseisky” subsoil area are presented in Table 7.

Fig. (4).

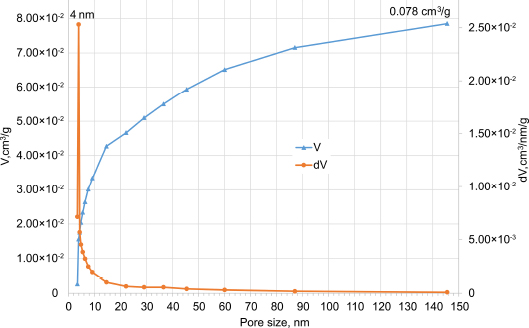
Differential and integral pore size distribution calculated for Portland cement concrete sample.

Table 4.
Input data of the added to concrete mixture water used in the simulation was obtained as the result of the analyses.
Parameter Temperature, °С рН Amount of Water, kg Concentration C×10 2 , mg/L
Al Ca Mg K Na Fe Cl
Measured value 25 7.23 0.67 10.40 68.90 3.62 44.90 23.40 2.30 5.00
Table 5.
Input data of the initial and resulting hydration solid phases of Portland cement concrete used in the basic simulation.
Primary Phases Chemical Formula in the Database Content, Moles Secondary Phases Chemical Formula in the Database Content, Moles
С3S (CaO)3SiO2 2.37 С4AClH10 Ca4Al2Cl2(OH)12(H2O)4 0***
C3A (CaO)3Al2O3 0.23 Hydrotalcite Mg4Al2O7(H2O)10 0.06
Anh CaSO4 0.18 Portlandite Ca(OH)2 4.18
Cal CaCO3 0.42 Ettringite ((H2O)2)Ca6Al2(SO4)3(OH)12(H2O)24 0.06
Dis-Dol CaMg(CO3)2 0.23 CSH3T-T2C ((CaO)0.75(SiO2)0.5(H2O)1.25)2 3.26
C4AF (CaO)4(Al2O3)(Fe2O3) 0.38 Monocarbonate Ca4Al2CO9(H2O)11 0.57
CA2 CaO(Al2O3)2 0.04 Fe(OH)3-llnl* Fe(OH)3 0.76
Portlandite Ca(OH)2 0.11 Cal CaCO3 0.31
Rankinite-llnl* Ca3Si2O7 0.05 [Neutral]** SiO2 27.21
C2S (CaO)2SiO2 0.80
[Neutral]** SiO2 27.21
* – database LLNL was used (for other – CEMDATA 18.1); ** – quartz sand filler is considered inert for dissolution during hydration; *** – less thermodynamically stable than other AFm-phases.
Table 6.
Characteristics of portland cement concrete were determined as a result of analyses and using the basic hydration simulation.
Obtained Parameters Experiment Simulation Relative Error, %
Density, g/cm3 1.91 2.16 13.09
Pore volume, cm3/g 0.078 0.081 3.85
Porosity θ 0.149 0.175 10.07
pH CWE 12.43 12.47 0.32
Direct measurement of the supernatant 12.38 0.73
Hydraulic conductivity, m/s 4.14×10-11 [34] 3.89×10-11 6.04
Table 7.
Predicted values of effective diffusion coefficients for Portland cement concrete obtained from simulation results.
Effective Diffusion Coefficient De×1012, m2/s
14С/14СО3 36Cl 135Cs 129I Other
13.44 22.40 23.52 9.30 11.20

The predicted values of effective diffusion coefficients of radionuclides obtained in Table 7 agree in order of magnitude with the literature data, and their deviations are associated with differences in the composition of concrete, porosity, and curing conditions. To confirm the obtained values and adjust the simulation, further studies are planned to experimentally determine the effective diffusion coefficients of radionuclides through the diffusion method using the “Yeniseisky” site synthetic groundwater as the aqueous phase.

CONCLUSION

As a result of this study, the phase composition of the cement binder and the concrete derived from it, along with the chemical composition of the water added to the mixture, were thoroughly analyzed. These data were essential for the parameterization of the basic hydration simulation of Portland cement concrete, which is being considered as a material for engineered barriers in the geological disposal facility. The simulation was developed to predict key filtration properties, such as porosity, hydraulic conductivity, and the pH of the pore solution, which are critical for ensuring the long-term safety and performance of the engineered barrier system.

The developed simulation of Portland cement concrete hydration demonstrated values for porosity, pH of the pore solution, and hydraulic conductivity that were in close agreement with the experimental data. This confirms the applicability of the simulation for predicting the initial characteristics of the filtration properties of the concrete. The minor discrepancies observed between the simulated and experimental results can be attributed to the lack of consideration of the hydration kinetics of the original cement. These discrepancies are primarily due to the presence of unreacted clinker minerals and variations in the phase composition, which were not fully accounted for in the current simulation. Addressing these factors will be the focus of future research, particularly in the context of predicting long-term changes in the EBS under the conditions of the GDF in the “Yeniseisky” subsoil area.

The predicted values of the effective diffusion coefficients for radionuclides, which pose the greatest threat to the biosphere, were calculated using the developed simulation. These values are consistent with the literature data, further validating the simulation's accuracy. However, to refine the simulation and confirm the predicted values, additional experimental studies are planned. These studies will involve the determination of effective diffusion coefficients using the through-diffusion method, with synthetic groundwater from the “Yeniseisky” site as the aqueous phase.

The findings of this study contribute to the broader understanding of the behavior of cement-based materials in the context of radioactive waste isolation. The ability to accurately predict the filtration properties of concrete is crucial for the design and optimization of engineered barriers in GDFs. The results also highlight the importance of considering the long-term interactions between the concrete and the surrounding geological environment, particularly in terms of chemical and physical changes that may occur over extended periods.

STUDY LIMITATIONS

It is important to acknowledge that this study has certain limitations, including the relatively small sample size, simplified hydration simulation, and the use of controlled laboratory conditions that may not fully represent the complex environment of a deep geological repository. Additionally, the focus on a specific set of radionuclides and short-term experimental data may affect the generalizability of the results. Future research should address these limitations by incorporating kinetic models, expanding the range of radionuclides, and conducting long-term experiments under more realistic conditions.

In conclusion, this work provides a solid foundation for further research into the long-term performance of cement-based barriers in GDFs. The developed simulation, while already showing promising results, will be further refined to account for the kinetics of cement hydration and the long-term evolution of the concrete's microstructure. This will enhance the accuracy of predictions regarding the filtration properties and overall performance of the engineered barriers, ultimately contributing to the safe and effective isolation of radioactive waste in geological disposal facilities.

AUTHORS’ CONTRIBUTION

It is hereby acknowledged that all authors have accepted responsibility for the manuscript's content and consented to its submission. They have meticulously reviewed all results and unanimously approved the final version of the manuscript.

LIST OF ABBREVIATIONS

BJH = Barrett-Joyner-Halenda model
CWE = Cold Water Extraction method
EBS = Engineered Barrier System
ESB = Engineered Safety Barrier
GDF = Geological Disposal Facility
HLW = High-level Waste
ICP-MS = Inductively Coupled Plasma Mass Spectrometry
ILW = Intermediate Level Waste
OPC = Ordinary Portland Cement
RW = Radioactive Waste
SKB = Svensk Kärnbränslehantering Aktiebolag
W/C = Water-to-Cement Ratio
XRD = X-ray Diffraction

CONSENT FOR PUBLICATION

Not applicable.

AVAILABILITY OF DATA AND MATERIALS

The data and supportive information are available within the article.

FUNDING

This study was funded by Rasotom State Atomic Energy Corporation, Rumia (50110008687).

CONFLICT OF INTEREST

The authors declare no conflict of interest, financial or otherwise.

ACKNOWLEDGEMENTS

Experimental studies were partially performed using equipment acquired with the funding of Moscow State University Development Program (X-ray Diffractometer Ultima-IV, Rigaku). The authors are grateful to I. Morozov (IGEM RAS) and S. Garanina (MSU) for their help in carrying out the study.

REFERENCES

1
"On the criteria for classifying solid, liquid and gaseous waste as radioact. waste, the criteria for classifying radioact. waste as special radioact. waste and as disposable radioact. waste, and the criteria for classifying disposable radioact", Available from: https://base.garant.ru/70247038/ [Accessed Oct. 21, 2024
2
"“On the handling of radioact. waste and on amendments to certain legislative acts of the Russian Federation.”", Available from: https://base.garant.ru/12187848/ [Accessed Oct. 21, 2024
3
"Disposal of radioact. waste. Principles, criteria and basic safety requirements", Available from: https://docs.secnrs.ru/ documents/nps/%D0%9D%D0%9F-055-14/%D0%9D%D0%9F-055-14_ris_%D0%BF%D1%80%D0%B8%D0%BA%D0%B0%D0%B7.pdf [Accessed Oct 21, 2024
4
K.V. Martynov, and E.V. Zakharova, "The analysis of localization and the scenario of evolution of DGDF for RW at the yeniseisky site (krasnoyarsk region)", Radioact. Waste, vol. 2, no. 2, pp. 52-62.
5
V. V. Krupskaya, E. A. Tyupina, S. V. Zakusin, O. A. Ilina, and E. A. Saveleva, "On the feasibility assessment of clay material application in the development of engineered safety barrier designs for deep geological RW disposal at the yeniseiskiy site", Radioact. Waste, vol. 2, no. 23, pp. 98-112.
6
B.T. Kochkin, V.I. Mal’kovskij, and S.V. Yudintsev, Nauchnye osnovy ocenki bezopasnosti geologicheskoj izolyacii dolgozhivushchih radioaktivnyh othodov (Enisejskij proekt)., IGEM RAS: Moscow, p. 384.
7
V.G. Rumynin, "Experience of Studying the Clay Masses and Crystalline Core-areas as Geological Environment for RW Final Isolation", Radioact. Waste, vol. 1, pp. 42-53.
8
IAEA, Disposal of radioact. waste. specific safety requirements no. SSR-5, . Available from: https://www-pub.iaea.org/ MTCD/Publications/PDF/Pub1449_web.pdf [Accessed Oct. 21, 2024
9
A. O. Pavliuk, S. G. Kotlyarevsky, R. I. Kan, A. G. Volkova, E. V. Zakcharova, A. N. Dorofeev, B. S. Zinnurov, and E. A. Komarov, "The dynamics of 14C and 36Cl radionuclide leaching from irradiated RBMK-1000 graphite in aqueous media and its analysis", Radioact. Waste, vol. 2, no. 19, pp. 35-48.
10
A. O. Pavliuk, S. G. Kotlyarevsky, R. I. Kan, A. G. Volkova, E. V. Zakcharova, M. A. Ilyukhina, V. B. Gorshkov, A. N. Dorofeev, B. S. Zinnurov, and E. A. Komarov, "Approaches to the characterization of graphite ugr blocks based on beta-emitting 14c and 36CL radionuclides testing at rbmk-1000-type reactors", Radioact. Waste, vol. 2, no. 15, pp. 21-32.
11
A.O. Pavlyuk, S.G. Kotlyarevskiy, R.I. Kan, A.G. Volkova, D.A. Zolotov, A.V. Pakhnevich, E.V. Zakharova, and A.A. Shiryayev, "Parameters of the porous irradiated graphite structure affecting the mechanisms associated with the release of long-lived radionuclides when exposed to liquid media and their identification", Radiochemistry, vol. 62, no. 6, pp. 526-535. [http://dx.doi.org/1031857/S003383112006009X
12
A.O. Pavlyuk, S.G. Kotlyarevskiy, R.I. Kan, A.G. Volkova, and E.V. Zakharova, "Experimental research on the longlived 14C and 36Cl radionuclide leaching from irradiated graphite", Radiochemistry, vol. 63, no. 2, pp. 149-159.
13
A. V. Talitskaya, E. V. Zakharova, N. D. Andryushchenko, and V. V. Bochkarev, "Long-term safety assessment for a radioactive waste disposal facility established during uranium graphite reactor decommissioning", Nucl. Radiat. Saf., vol. 2, no. 84, pp. 54-60.
14
C. Bucur, C. Ichim, and I. Florea, "14 C Release from TRIGA irradiated graphite", Radiocarbon, vol. 60, no. 6, pp. 1819-1829.
15
D. Grigaliuniene, P. Poskas, R. Kilda, and A. Narkuniene, "Preliminary investigation of 14 C migration from RBMK-1500 reactor graphite disposed of in a potential geological repository in crystalline rocks in Lithuania", Radiocarbon, vol. 60, no. 6, pp. 1839-1848.
16
N.S. Tsebakovskaya, S.S. Utkin, I.V. Kapyrin, N.V. Medyantsev, and A.V. Shamina, Review of foreign practices for disposal of spent nuclear fuel and radioact. waste., Komtechprint: Moscow, p. 208.
17
E.A. Tyupina, P.P. Kozlov, and V.V. Krupskaya, "Application of cement-based materials as a component of an engineered barrier system at geological disposal facilities for radioactive waste—a review", Energies, vol. 16, no. 2, p. 605.
18
K.A. Boldyrev, "Aspects of modeling of the degradation of engineered safety barriers based on portland cement in radionuclide migration problems", Radiochemistry, vol. 66, no. 2, pp. 253-267.
19
D.E. González-Santamaría, R. Fernández, A.I. Ruiz, A. Ortega, and J. Cuevas, "Bentonite/CEM-II cement mortar INTERFACE EXPERIMENTS: A proxy to in situ deep geological repository engineered barrier system surface reactivity", Appl. Geochem., vol. 117, p. 104599.
20
M.C. Alonso, G.J.L. Calvo, J. Cuevas, M.J. Turrero, R. Fernández, E. Torres, and A.I. Ruiz, "Interaction processes at the concrete-bentonite interface after 13 years of FEBEX-Plug operation. Part I: Concrete alteration", Phys. Chem. Earth Parts ABC, vol. 99, pp. 38-48.
21
R. Fernández, E. Torres, A.I. Ruiz, J. Cuevas, M.C. Alonso, G.J.L. Calvo, E. Rodríguez, and M.J. Turrero, "Interaction processes at the concrete-bentonite interface after 13 years of FEBEX-Plug operation. Part II: Bentonite contact", Phys. Chem. Earth Parts ABC, vol. 99, pp. 49-63.
22
G.J.L. Calvo, A. Hidalgo, C. Alonso, and F.L. Luco, "Development of low-pH cementitious materials for HLRW repositories", Cement Concr. Res., vol. 40, no. 8, pp. 1290-1297.
23
V.S. Gupalo, "Technological issues of increasing the safety of historical radioact. waste storage facilities", Mount. Infor. Analyt. Bull., vol. 9, pp. 112-116.
24
L.O. Höglund, and A. Bengtsson, "Some chemical and physical processes related to the long-term performance of the SFR repository", Available from: https://inis.iaea.org/collection/NCLCollectionStore/_Public/31/008/31008587.pdf [Accessed Oct. 21, 2024].
25
V. V. Krupskaya, D. V. Biryukov, P. E. Belousov, V. A. Lekhov, A. Yu. Romanchuk, and S. N. Kalmykov, "The use of natural clay materials to increase the nuclear and radiation safety level of nuclear legacy facilities", Radioact. Waste, vol. 2, no. 3, pp. 30-43.
26
V. V. Krupskaya, S. V. Zakusin, V. A. Lekhov, O. V. Dorzhieva, P. E. Belousov, and E. A. Tyupina, "Buffer properties of bentonite barrier systems for radioact. waste isolation in geological repository in the nizhnekanskiy massif", Radioact. Waste, vol. 1, no. 10, pp. 35-55.
27
"Safety functions, performance targets and technical design requirements for a KBS-3V repository Conclusions and recommendations from a joint SKB and Posiva working group", Available from: https://skb.com/publication/2485568/Posiva+SKB+Report+01.pdf [Accessed Oct. 21, 2024].
28
S. A. Bogatov, "HLW disposal of in verticale deposition holes with cement backfill — pro and contra with regard to long term safety of geological disposal facility", Radioact. Waste, vol. 1, no. 2, pp. 21-33.
29
C. Bao, G. Jiaxing, and Z. Huixin, "Alteration of compacted GMZ bentonite by infiltration of alkaline solution", Clay Miner., vol. 51, no. 2, pp. 237-247.
30
O. Karnland, S. Olsson, U. Nilsson, and P. Sellin, "Experimentally determined swelling pressures and geochemical interactions of compacted Wyoming bentonite with highly alkaline solutions", Phys. Chem. Earth, Parts., vol. 32, no. 1-7, pp. 275-286.
31
W.M. Ye, Z.J. Zheng, B. Chen, Y.G. Chen, Y.J. Cui, and J. Wang, "Effects of pH and temperature on the swelling pressure and hydraulic conductivity of compacted GMZ01 bentonite", Appl. Clay Sci., vol. 101, pp. 192-198.
32
M.C. Alonso, G.J.L. Calvo, C. Walker, M. Naito, S. Pettersson, I. Puigdomenech, M.A. Cunado, M. Vuorio, H. Ueda, and K. Fujisaki, "Development of an accurate PH measurement methodology for the pore fluids of low PH cementitious materials", Available from: https://skb.se/upload/publications/pdf/R-12-02.pdf [Accessed Oct. 21, 2024].
33
A.N. Dorofeev, L.A. Bolshov, I.I. Linge, S.S. Utkin, and E.A. Saveleva, "Strategic master plan for R&D demonstrating the safety of construction, operation and closure of a deep geological disposal facility for radioact. waste,", Radioact. Waste, vol. 1, pp. 32-41.
34
L. Wissmeier, and D.A. Barry, "Effect of mineral reactions on the hydraulic properties of unsaturated soils: Model development and application", Adv. Water Resour., vol. 32, no. 8, pp. 1241-1254.
35
V. Picandet, D. Rangeard, A. Perrot, and T. Lecompte, "Permeability measurement of fresh cement paste", Cement Concr. Res., vol. 41, no. 3, pp. 330-338.
36
A. Idiart, J. Olmeda, and M. Laviña, Modelling of concrete degradation – influence of concrete mix design. Report for the safety evaluation SE-SFL, . Available from: https://www.skb.com/publication/2493347/R-19-14.pdf [Accessed Oct. 21, 2024].
37
F. Deby, M. Carcassès, and A. Sellier, "Probabilistic approach for durability design of reinforced concrete in marine environment", Cement Concr. Res., vol. 39, no. 5, pp. 466-471.
38
G. Sun, Y. Zhang, W. Sun, Z. Liu, and C. Wang, "Multi-scale prediction of the effective chloride diffusion coefficient of concrete", Constr. Build. Mater., vol. 25, no. 10, pp. 3820-3831.
39
J. Liu, M. Löfgren, and I. Neretnieks, "Data and uncertainty assessment. matrix diffusivity and porosity in situ", Available from: https://inis.iaea.org/collection/NCLCollectionStore/_Public/38/088/38088526.pdf [Accessed Oct. 21, 2024].
40
B. Allard, S. Eliasson, S. Höglund, and K. Andersson, "Sorption of Cs, I and actinides in concrete systems", Available from: https://skb.com/publication/3189/TR84-15_OCR.pdf [Accessed Oct. 21, 2024].
41
"Methods for strength determination using reference specimens", Available from: https://www.russiangost.com/p-71067-gost-10180-2012.aspx. [Accessed Oct. 21, 2024].
42
J.E. Post, and D.L. Bish, "Rietveld refinement of crystal structures using powder X-ray diffraction data", Mod. Powd. Diffract., vol. 20, pp. 277-308.
43
N. Doebelin, and R. Kleeberg, "Profex : A graphical user interface for the Rietveld refinement program BGMN", J. Appl. Cryst., vol. 48, no. 5, pp. 1573-1580.
44
K. Scrivener, R. Snellings, B. Lothenbach, Eds., A practical guide to microstructural analysis of cementitious materials., Crc Press: Boca Raton, FL, USA, p. 540.
45
G. Plusquellec, M.R. Geiker, J. Lindgård, J. Duchesne, B. Fournier, and D.K. Weerdt, "Determination of the pH and the free alkali metal content in the pore solution of concrete: Review and experimental comparison", Cement Concr. Res., vol. 96, pp. 13-26.
46
E.M. Gartner, F.J. Tang, and S.J. Weiss, "Saturation factors for calcium hydroxide and calcium sulfates in fresh Portland cement pastes", J. Am. Ceram. Soc., vol. 68, no. 12, pp. 667-673.
47
P.H.R.E.E.Q.C. Version, "PHREEQC version 3 | U.S. geological surve", Available from: https://www.usgs.gov/software/phreeqc-version-3 [Accessed Oct. 21, 2024].
48
P.P. Kozlov, and E.A. Tyupina, "Development of a laboratory setup for determining the filtration coefficient and mineral transformations of advanced concretes when organizing engineered safety barriers in the conditions of the GDF",
49
Z. Szántó, É. Svingor, M. Molnár, L. Palcsu, I. Futó, and Z. Szűcs, "Diffusion of 3H, 99Tc, 125I, 36Cl and 85Sr in granite, concrete and bentonite", J. Radioanal. Nucl. Chem., vol. 252, no. 1, pp. 133-138.