All published articles of this journal are available on ScienceDirect.
Heat Transfer Modeling in Bone Tumour Hyperthermia Induced by Hydroxyapatite Magnetic Thermo-Seeds
Abstract
Background:
Hyperthermia is an adjuvant oncologic thermal therapy. In the case of deep-seated bone cancers, the interstitial hyperthermia treatment can be performed using thermo-seeds, implanted biomaterial components that are able to convert external electromagnetic power into thermal one. Several magnetic biomaterials have been synthesized for thermal treatments of cancer. However, less attention has been paid to the modeling description of the therapy, especially when the bio-heat transfer process is coupled to the electromagnetic heating.
Objective:
In this work, a comparison between the available analytical and numerical models is presented.
Methods:
A non-linear multiphysics model is used to study and describe the performance of cylindrical magnetic hydroxyapatite thermo-seeds to treat residual cancer cells of bone tumours.
Results:
The thermal dynamics and treatment outcome are carefully evaluated. Under the exposure of a magnetic field of 30 mT, working at 300 kHz, it was found that magnetic hydroxyapatite implants with a size of 10 mm × 10 mm could increase the temperature above 42 °C for 60 min.
Conclusion:
The proposed model overcomes the limitations of the available theoretical frameworks, and the results reveal the relevancy of the implant geometry to the effectiveness of the hyperthermia treatment.
1. INTRODUCTION
Bone cancers are neoplasms that can affect relatively young subjects (with age between 10 and 25 years old) with an incidence and survival rate of about 35% [1]. Bone tumours are classified depending on the tissue of origin. The preferred sites of origin are the extremities of long bones. Among the malignant neoplasms, two of the most relevant targets in orthopedic oncology are the Osteosarcomas (OS) and the Fibrosarcomas (FS). These aggressive cancers cause impairment and pain to the patients, thus ruining their quality of life [1, 2]. Furthermore, their pathologic, chaotic and fast growth damages lead to healthy bone tissue fracturing. Hence, following the diagnosis, early and effective countermeasures must be sought to prolong the patient prognosis [1]. Currently, surgical intervention is the gold-standard. In particular, osteotomies and resection procedures are carried out to try to directly eliminate cancer cells [2]. However, since the margin of the tumours is often not well defined, the recurrence rate can be around 15% [1, 2]. Moreover, as a consequence of osteoteomies, additional damages to the bone are produced, and a surgical gap is seen after the intervention. From a clinical perspective, an auto- or allogeneic graft, or a synthetic biomaterial (e.g. bone cement, bioglasses, a bioceramic or a polymer) is required to restore the functionality of the bone tissue [1, 2].
All these limitations lead to the investigation and testing of innovative and less invasive therapies [3]. As preferred for other kinds having tumours, the so-called neo-adjuvant chemotherapy and radiotherapy have been studied [2, 3]. However, the high systemic toxicity of drugs and the radio-resistance of bone cancers, especially OS, limit the effectiveness of these novel approaches [1, 2]. Therefore, in order to improve the aforementioned clinical strategies, hyperthermia treatment (HT) was proposed [3]. HT is a thermal therapy used in oncology and its goal is to increase the temperature of the given cancer tissue from 37 °C to 42 °C-45 °C for at least 60 min [3-5]. The effect of this temperature increase is the damaging of cell proteins, and the irreversible modification of the DNA repair mechanisms, while the local blood flow and sensitivity to chemotherapy and radiotherapy are also increased [3]. Hyperthermia can be induced in several ways, e.g. using ultrasounds (US) or electromagnetic (EM) energy [6]. In the case of bone tumours, the use of US is discouraged by their poor effectiveness, which is due to the less penetration depth and the significant reflection at the bone interface [6]. Regarding EM-based hyperthermia devices for orthopaedic oncology purposes, applicators working in the microwave frequency bands for medical application (i.e. 434 MHz, 915 MHz, 2.45 GHz) demonstrated poor effectiveness and drawbacks [6], even though the target tumour tissue was directly exposed to the radiation during the intervention [5-7]. However, the possibility of using radio-frequency (RF) magnetic fields (MF) to perform the hyperthermia treatments is now widely investigated [8]. Indeed, given a working frequency of hundreds of kHz, and the transparency of the body tissues, magnetic hyperthermia (MHT) ensures a higher penetration depth of the field and allows to treat deep-rooted tumours, with reduced overheating of the non-target healthy tissues [5-9]. Considering the urgent and fundamental clinical requirement of having a prosthetic implant, and given the potentialities and advantages of MHT, the possibility of implanting a magneto-responsive material, to be used both as tissue scaffold and as thermo-seed to perform the interstitial and local thermal therapy, was investigated [4]. A schematic representation of the rationale of such an approach is presented in Fig. (1). In particular, at first, the use of ferromagnetic cylindrical bars, inserted in the operated tumour margins, and heated under the action of an external MF, was tested [10]. However, poor biocompatibility may limit this form of MHT. Therefore, a plethora of magnetic biomaterials has been developed [4, 5, 9]. The synthesis of nanocomposites of magnetic nanoparticles (MNPs), polymers or ceramics (for example, using dip-coating or impregnation methods), or the manufacturing of iron-doped bioceramics, is currently under study [9]. Magnetic implants for bone tumour hyperthermia were developed using ferromagnetic or superparamagnetic nanoparticles [5]. The former kind of MNPs has an average particle radius higher than 250 nm, it presents a non-zero coercive field, and its heat losses are related to the hysteresis phenomenon [4, 10]. On the other hand, the latter kind of particles has typical dimensions below 25 nm, does not present a residual magnetization, and the heat is generated by the fluctuations of the dipole moment in response to a time-varying magnetic field [5]. The superparamagnetic MNPs are the most suitable candidates for the synthesis of magnetic thermo-seeds [4, 5]. Moreover, considering the in vivo implantation, the long-term stability and the mechanism of interaction with the tissue are pivotal aspects [4]. The magnetic bioactive ceramic, which was considered in this work, is an osteoconductive biomaterial, which means that, when implanted, it is capable of releasing ions which create a firm apatite layer at the interface with the surrounding tissues, as already experimentally demonstrated in the literature [11-13]. Furthermore, the presence of iron increases the porosity, which can act as a topological stimulus for the osteogenic cells, and can enhance the stiffness of the biomaterials, i.e. increasing their Young’s modulus. All these properties allow estimating the in-vivo life span of the implant to be longer than 12 weeks [13].
Despite the research interest in the morphological, chemical and biochemical characterization of such a functional nanocomposite, the theoretical and engineering aspects, related to its possible (and optimal) use as an interstitial hyperthermia agent, have not yet been fully investigated. Recently, the heat dissipation mechanism of magnetic implants, produced using superparamagnetic MNPs, was investigated at working frequencies from 100 kHz to 700 kHz [5, 11]. The non-linear nature of the HT was first elucidated [14-16]. The authors highlighted, through the multi-physics simulations of a spherical magnetic implant, exposed to a RF magnetic field, that as the temperature of the system at the nanoparticles location increases, their magnetic susceptibility decreases, due to the enhancement of the thermal energy barrier increases. Therefore, the tendency of the thermo-seed to dissipate heat decreases as the system temperature increases, reaching a quasi-steady state regime. Even though peculiar anatomical cases were numerically investigated by Lodi et al. [17], the implant geometry has been considered in a simplified way. It should be pointed out that for clinical and practical cases, the synthetic bone grafts can have complex forms and shapes, but the minimal and most fit shape for an orthopaedic application is that of a cylinder [4, 10]. Therefore, in this paper, the non-linear and multiphysics model [14, 17] is modified to account for the heat transfer aspects and solved, using a commercial Finite Element Method (FEM) software for the case of a cylindrical magnetic implant of hydroxyapatite, in order to define a set of geometric and operative parameters for the hyperthermia treatment, using these novel thermo-seeds.
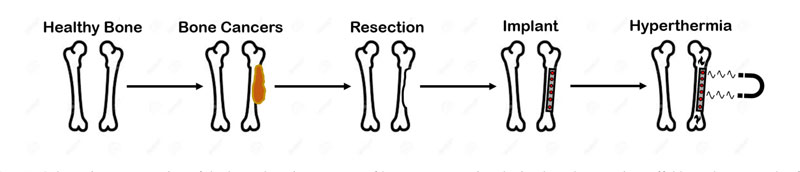
2. MATERILAS AND METHODS
2.1. Modeling the Hyperthermia Treatment
The heat transfer phenomenon in biological systems can be described by the microscopic energy balance equation in the form derived by Pennes for a perfused tissue [10, 18]:
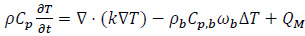 |
(1) |
where T stands for the temperature field, ρ and Cp are the tissue density (kg·m -3) and the specific heat capacity at constant pressure (Jkg -1K -1), respectively. The term Qm is the metabolic heat rate, i.e. the heat per volume unit that is dissipated by the living cells, in W·m -3. The term ρbCp,bωb ΔT models the blood perfusion in the biological tissues. The variables ρb, Cp,b and ωb indicate blood density (kg·m -3), specific heat (Jkg -1K -1) and tissue perfusion (s -1), respectively [18]. The architecture of small vessels and capillaries has a primary role in the thermal homeostasis of a tissue [18]. Indeed, if the temperature is lower than T b = 37 °C, since ΔT = T-Tb, the perfusion increases the input heat flux, trying to increase the temperature. On the other hand, if the system temperature overcomes the value of Tb, the perfusion term in Eq. (2) is negative and the capillaries act as a sink, removing the excessive heat in order to decrease the tissue temperature.
This last scenario coincides with the non-physiological conditions which are induced for therapeutic purposes during the hyperthermia treatment [5-8, 10, 14, 17, 18]. For the case of HT using magnetic implants, the dynamic and spatial evolution of the temperature distribution, in both the target and the non-target tissues, can be measured by calculating the power which is transmitted during the RF exposure. The presence of an external EM field forcing the system can be included in Eq. (1) as follows:
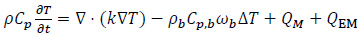 |
(2) |
where QEM includes the power per volume unit, which is dissipated by the dielectric losses in tissues (P e), due to induced RF currents, and the power which is stored and dissipated in the magnetic implant (P m). In mathematical terms:
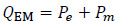 |
(3) |
From a theoretical point of view, the exact and closed-form solution of the partial differential equation (Eq. (2)) is not trivial [19]. However, under some assumptions and simplifications, the thermal field can be found. In particular, the case of a cylindrical implant with a spherical cross-section, with radius r sc and volume Vimplant, was investigated [10]. The tumour tissue was assumed to be a spherical and homogeneous region surrounding the implant. By neglecting QM, assuming ρ, C p and k to be constants, and considering the final temperature increase as the final outcome of the HT, Eq. (2) can be solved using the steady-state limit to obtain the following radial 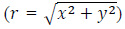 distribution outside the implant [10]:
distribution outside the implant [10]:
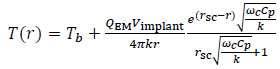 |
(4) |
A limit of this solution is that it is derived considering a constant value of QEM and neglecting the spatial distribution of the EM power losses in the implant and tumour regions. Furthermore, the steady-state solution does not allow to investigate the system evolution during the whole treatment time, which can last from 60 to 80 min. Since the goal of the HT is to increase the temperature of neoplastic cells without harming or damaging the healthy tissues, it is of interest to monitor the possible transient burst of temperature, which may occur in the non-target regions [5, 6, 8, 10]. To overcome the limitations of the model by Stauffer et al. [10], Bagaria and Johnson derived an analytical solution of the unsteady bio-heat transfer problem for a two-layered geometry (which represents the tumour and the healthy tissue) when the deposited EM power has a second-order polynomial dependence on space [19, 20]. The temperature evolution in the tumour region is a Fourier series, as follows [20]:
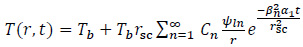 |
(5) |
where Cn, ψln, βn and α1 are functions of index n and of the implant radius r sc, and r indicates the radial position [18].
Eq. (5) is derived assuming that neither the electromagnetic properties of the tissue or implant, nor the thermal properties significantly vary with the temperature. Furthermore, another rather limiting feature is the simplified description of the implant geometry and of the pattern of the input power. Therefore, in the literature, some numerical and multi-physic approaches have been investigated in order to refine the modeling and planning of the HT of bone tumours using magnetic scaffolds [14-17]. In particular, the coupling between electromagnetic and thermal fields is a pivotal aspect of the simulation of the HT therapy. In this paper, the non-linear model from [14-17] is modified to deal with the magnetic implant of cylindrical shape.
3. THE MULTIPHYSIC MODEL
3.1. The Problem Geometry
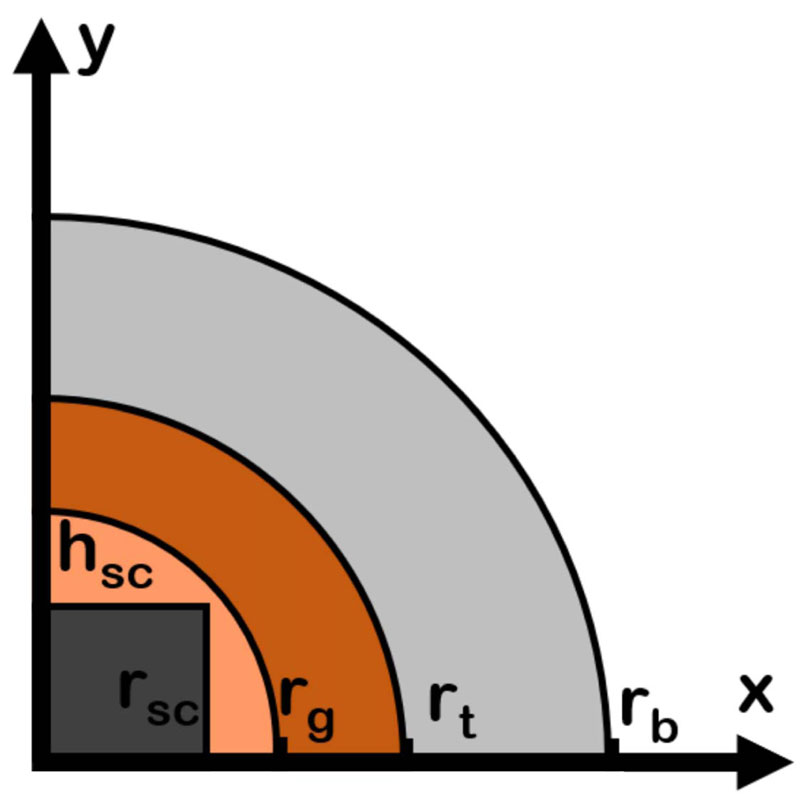
The first modification and improvement of the available literature models is the definition of geometry. A 2D cross-section of a long bone is considered since the occurrence of bone tumours in this anatomical site is relatively high.
(~40%) [1, 2]. A cylindrical scaffold of height h sc and radius r sc is supposed to be implanted as a graft following the resection of a bone tumour, as shown in Fig. (2). The typical dimension of a scaffold ranges from 2.5 mm to 10 mm [4]. Therefore, the analysis can be restricted to a narrow region around the implant since heating is a relatively local phenomenon [17]. Therefore only the main tissues are considered, as shown in Fig. (2). The center of the XY-axes reference system coincides with the scaffold center. From the center outwards, three different biological materials can be identified. Nearby the magnetic implant, a circular surgical fracture gap with radius r g = 13 mm is present [2]. The surgical gap is a heterogeneous mixture of tissues (bone and blood) and proteins. A circular area of radius r t = 13.5 mm, containing the residual bone tumour cells, is supposed to surround the fracture gap. This region models the unclear and ambiguous margin, which can be occasionally left after the surgical intervention, i.e. the cause of the high recurrence for OS and FS tumours. Finally, the healthy bone tissue with thickness r b-r t = 22 mm is considered, as shown in Fig. (2).
The geometry presented in Fig. (2), given the spatial symmetry reason, is a fourth of the entire domain, and only the first is considered to lower the computational burden due to the coupled and non-linear nature of the multiphysics problem. The proposed geometry is different from those of the cited literature, since the previous works considered a simple circular scaffold with a fixed dimension r sc = 5 mm [14-17]. The investigation of an implant with a cylindrical shape is a rather critical point for practical applications [2, 4]. However, in the literature, the influence of the geometrical parameters of the implant on the hyperthermia treatment is often neglected or poorly investigated, being [10] the only one, and not recent, exception.
3.2. Electromagnetic Aspects
Another difference between the proposed model and the previous theoretical approaches [10, 18] is in the exact computation of the input and stored EM power distributions, due to the exposure to the RF magnetic field during the hyperthermia treatment. The two-dimensional pattern of EM power losses can be derived from the computation of the magnetic field, 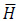 (Am -1), and of the electric field,
(Am -1), and of the electric field, 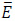 (Vm -1), which are the unknown vectors of Maxwell’s equations [7]:
(Vm -1), which are the unknown vectors of Maxwell’s equations [7]:
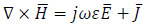 |
(6) |
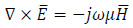 |
(7) |
where ω = 2pf is the angular frequency, ε is the dielectric permittivity of the medium, in Fm -1, which are reported in Tab. 1, and µ is the magnetic permeability of the medium, in Hm -1. The power which is stored in the tissues by the eddy currents can then be calculated by the induced electric field, according to the Faraday’s law in the low-frequency regime, i.e.
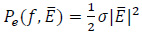 |
(8) |
where σ is the electrical conductivity, in Sm -1, of the medium or tissue. On the other hand, the heat dissipation by the magnetic implant is modeled considering that the magnetic permeability is a complex variable, i.e. that 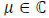 and hence µ = µ' - jµ'', where j is the imaginary unit. The imaginary or out-of-phase component of the magnetic permeability allows to calculate the power that is dissipated by the magnetic implant as follows [5, 14, 17]:
and hence µ = µ' - jµ'', where j is the imaginary unit. The imaginary or out-of-phase component of the magnetic permeability allows to calculate the power that is dissipated by the magnetic implant as follows [5, 14, 17]:
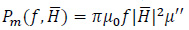 |
(9) |
In this work, Eq.s (6) and (7) are solved, considering that a homogeneous external magnetic field H0 is applied along the x-axis of the geometry in Fig. (2). It is worthy of mention that, even though a homogeneous initial field distribution is considered, the  and
and 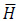 fields are not homogeneous too, due to the presence of the magnetic biomaterial and tissues with different dielectric permittivity [17]. Therefore, the total EM dissipated power (Q EM) is not homogeneously distributed and could hardly be described by a second-order polynomial function for the geometry under analysis [18-24].
fields are not homogeneous too, due to the presence of the magnetic biomaterial and tissues with different dielectric permittivity [17]. Therefore, the total EM dissipated power (Q EM) is not homogeneously distributed and could hardly be described by a second-order polynomial function for the geometry under analysis [18-24].
3.3. Non-linear Properties of Magnetic Scaffolds
When the magnetic implant is exposed to the external RF magnetic field at the frequency f, the MNPs, which are embedded in the biomaterial, dissipate heat due to the Néel relaxation [4, 5]. Such heat is conducted from the MNPs to the biomaterial matrix; then it diffuses to the surrounding tissues [15]. This power increases the temperature T to reach the therapeutic levels for the HT. As the temperature changes, the physical mechanism of the heat dissipation is no longer constant [5, 11, 14, 17]. As a consequence, any model, intended for the treatment planning, should deal with the temperature-dependent nature of the dissipation mechanism which is due to the magnetic implant that is manufactured having incorporated superparamagnetic nanoparticles [21-23], such as the magnetic hydroxyapatite implant, which was synthesized by Tampieri and colleagues [12, 13], that is the object of this study, and the properties of which are reported in Tab. 3.2.
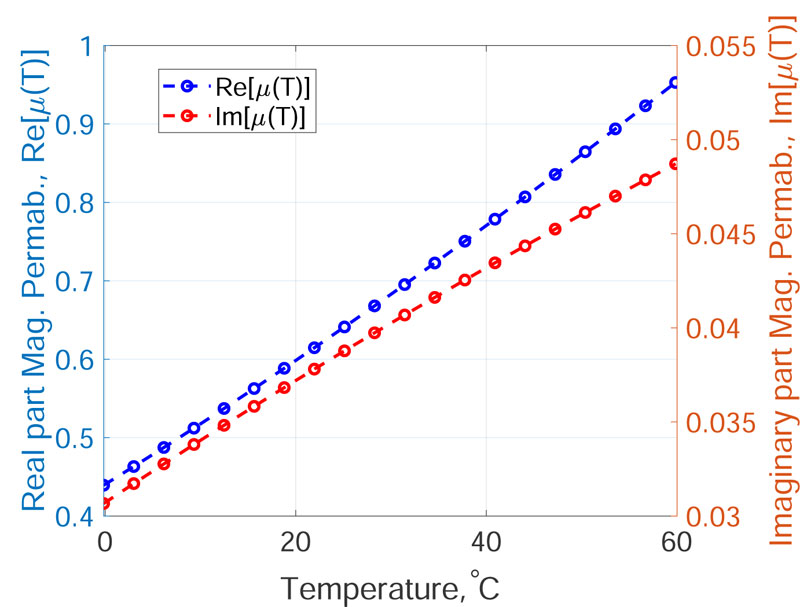
As found in some studies [14, 17], the magnetic permeability of the thermo-seeds is a function of both the working frequency of the applied MF and the system temperature, i.e.µ = µ(f,T). Regarding the frequency response of the magnetic permeability, for a fixed temperature, the in-phase and out-of-phase component can be evaluated using the Cole-Cole model [11]:
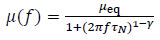 |
(10) |
where µeq is the initial or equilibrium magnetic permeability of the MNPs population, and it is inversely proportional to the system temperature [11, 17, 24]. In Eq. (10), 4N is the characteristic Néel relaxation time of the magnetic dipole moment of the nanoparticles [25]:
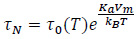 |
(11) |
where τ0 is a pre-exponential factor, which is a function of the system temperature [16, 17]. The Néel relaxation time (Eq. (11)) is also influenced by the ratio of the particles energy (i.e. the product of particle anisotropy energy per volume unit, Ka and its volume, Vm) to the thermal energy (i.e. the product of the Boltzmann’s constant, kB, and the system temperature, T) in a non-linear way. As a matter of fact, the physical framework which describes the heat dissipation of magnetic implants is a rather complex one, then the numerical simulations of the HT treatment present a relatively high computational burden.
The magnetic hydroxyapatite thermo-seeds have been tested by other researchers under simplified experimental conditions, characterized and simulated at the working frequency of 300 kHz [11, 14-17, 26, 27]. Therefore, in this paper, the working frequency was chosen to be 300 kHz; the magnetic properties are considered to be a function of the system temperature, i.e.µ = µ(T). Since the temperature-dependent variation of the magnetic permeability is described by highly non-linear relationships, and depends on several parameters, an engineering approach could reduce the computational burden, which is required to perform the multiphysics simulation of the bone tumours HT. Therefore, in order to simplify the model of the hyperthermia treatment using magnetic biomaterials, without losing any physical insight, the following empirical model for the temperature dependence of the magnetic permeability of the implant is proposed in the temperature range of the hyperthermia treatment (37 °C-60 °C):
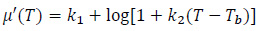 |
(12) |
where k1 = 0.3 and k2 = 0.0129 °C -1. For the imaginary (out-of-phase) part of the magnetic permeability, the variation with respect to T can be assumed to be linear, i.e.
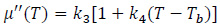 |
(13) |
where k3 = 0.002 K -1, k4 = -0.19. The coefficients of Eq.s (12) and (13) are found fitting the data shown in Fig. (1) at page 296 of the work by Fanti et al. [14], using the non-linear least square routine of Matlab (The MathWorks Inc., Natick, MA, USA). The µ'(T) and µ'' (T) curves for the magnetic hydroxyapatite scaffold with properties from Tab. 3.2 are presented in Fig. (3).
3.4. Temperature Dependence of Dielectric and Thermal Properties
According to the literature [28, 29], the dielectric and thermal properties of tissues are known to vary as a function of the temperature in the hyperthermia range, i.e. from 37 °C to 60 °C (Tables 1 and 2 ) [26]. In particular, the vascular parameters of the Pennes equation (Eq. (2)) are dependent on the temperature [18, 21, 22, 30]. This relevant feature of the physics of the thermal treatment under study adds non-linearity to the multiphysics model for the hyperthermia treatment analyzed here. To account for this dependence in the model, a linear relationship between the EM and thermal properties can be assumed [28]. Therefore, indicating Г the generic physical property (i.e. ε, σ, k, C p, ρ), the following equation form was used to compute the value for the given system temperature T [17]:
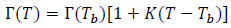 |
(14) |
| εr | η, Sm -1 | |
| Magnetic Hydroxyapatite (MHA) | 12.5 | 2·10 -3 |
| Surgical gap | 3580 | 0.55 |
| Tumour | 195 | 0.196 |
| Cortical Bone | 190 | 0.02 |
| Property | Value |
| MNPs mean radius | 10 nm |
| MNPs volumetric fraction | 3% |
| Saturation magnetization | 0.95 emu·g -1 |
| Max. Temp. | 40 °C |
| Time | 1 min |
| Magnetic field | 20 kAm -1 |
| Frequency | 300 kHz |
where Г(Tb) is the value of the property at 37 °C, as reported in Tab. 1 and 3.3. The values of the coefficients K were assumed to be equal to 3% K -1 for both the permittivity and the electrical conductivity of biological tissues. On the other hand, for thermal conductivities, K=0.5% K -1, whilst for the heat capacity, the coefficients were set to 0.33% °C -1 [16, 17]. As regards the variation of the perfusion of healthy and tumour tissues with the temperature, the piecewise model of Lodi et al. was implemented [17]. In particular, the variation in the healthy tissue blood perfusion can be normalized to its value at 37 °C in order to be applied to any tissue with the geometry of Fig. (2) [17, 18]:
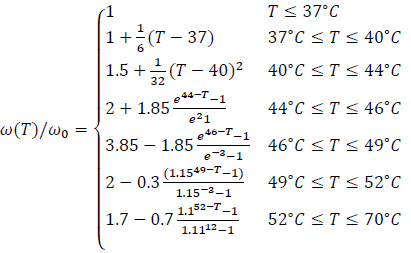 |
(15) |
For the tumour tissue, the relative temperature variation is rather different and can be evaluated using the following piecewise model [17, 18]:
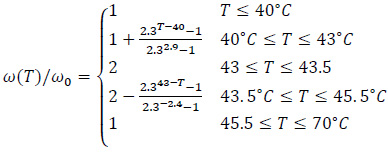 |
(16) |
3.5. Thermal Dose and Therapy Assessment
Provided that the proposed model aims at describing the heat transfer during the hyperthermia treatment of bone tumours using magnetic implants, it is necessary to introduce some figures of merit for the treatment outcome, i.e. the effectiveness of the thermal therapy under analysis. As discussed in the introduction, the temperature is a relevant parameter for the quality of interstitial HT [4, 31]. For the residual bone tumour cells, a thermal treatment at about 43 °C for 60 min is recommended [1-4, 11, 14-17]. Despite the focus on the target tissue, the temperature field and the time of exposure to the heat source must be controlled in the healthy non-target tissues, such as the surrounding bone, to avoid overheating, burns, toxicity or any embolic events [31, 32]. Bone cells undergo necrosis if the temperature of 47 °C is reached and kept for 1 min [17]. Therefore, in this work, as an outcome of the treatment, the temperature, averaged over the tissues volume of the geometry shown in Fig. (2), and over time, was investigated.
Besides the average temperature in a tissue, a clinically relevant figure of merit is the CEM43, i.e. the thermal dose, for a given time, necessary to produce damage which is equivalent to the damage which could be procured by exposing the tumour tissue at 43 °C for 60 min [33]:
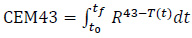 |
(17) |
where R is the cell death rate. In particular, R is equal to 0.5 when T>43 °C, whereas R = 0.25 if 39 °C≥T≥43 °C and, finally, R=0 for T<39 °C. The cell death rate is constant over the aforementioned temperature intervals. The higher the CEM43 in the target tissue, the better the treatment outcome. As a matter of fact, this physical quantity should be as lower as possible in the non-target tissues.
4. RESOLUTION SCHEME
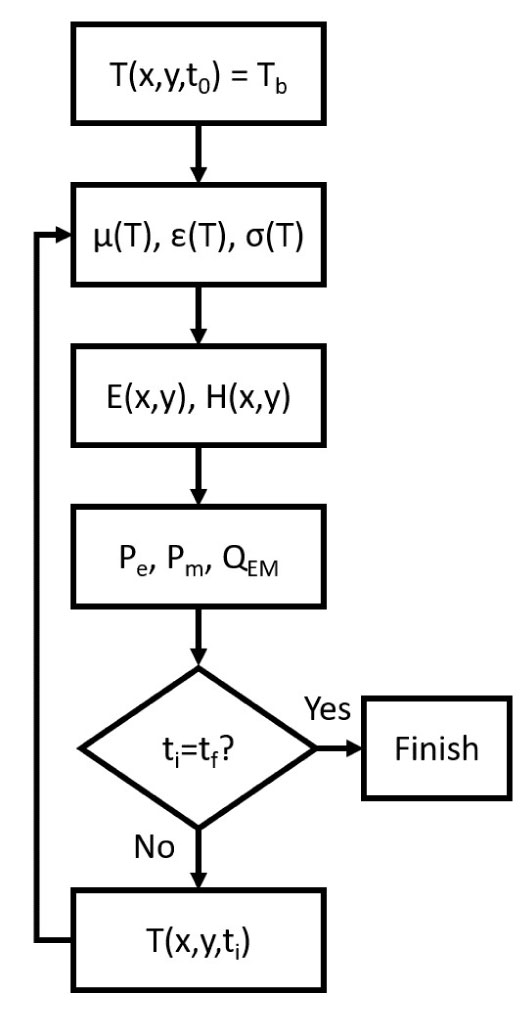
The commercial FEM software Comsol Multiphysics v5.5 (Comsol Inc., Burlington, MA, USA) was used to simulate the hyperthermia treatment of bone tumours using magnetic scaffolds as thermo-seeds. The coupled electromagnetic and thermal problems were solved, as summarized in Fig. (4).
Assuming a homogeneous initial temperature distribution, the magnetic properties of the implant and tissues were evaluated by using Eq.s (12) and (13). Then Maxwell’s equations were solved in the frequency domain using the AC/DC module [17, 34]. The power which is stored and dissipated by the magnetic implant was derived by using Eq.s (9), whilst the dielectric losses were computed using Eq. (8). The overall electromagnetic power QEM was obtained according to Eq. (3). After the evaluation of the thermal properties at the current temperature, the new temperature distribution at the following time step was evaluated through Eq. (2) by means of the Bio-Heat Transfer module. The temperature distribution was used to calculate the new value of the EM properties and then the resolution steps were repeated until the final time, t f, was reached.
By using the resolution scheme in Fig. (4), the hyperthermia treatment of the residual bone tumour cells was simulated for 100 min for a cylindrical prosthesis with variable dimensions. The volume fraction of MNPs in the biomaterial was kept at a constant value (see Tab. 3.2) and the electromagnetic properties were assumed to follow the proposed model. Considering that the biological target is a 0.5 mm thick annular region of residual tumour cells, the height (h sc) and the radius (r sc) of the implant varied from 2.5 mm to 10 mm, with a 2.5 mm interval, therefore, sixteen combinations of the possible implant size were tested.
5. RESULTS
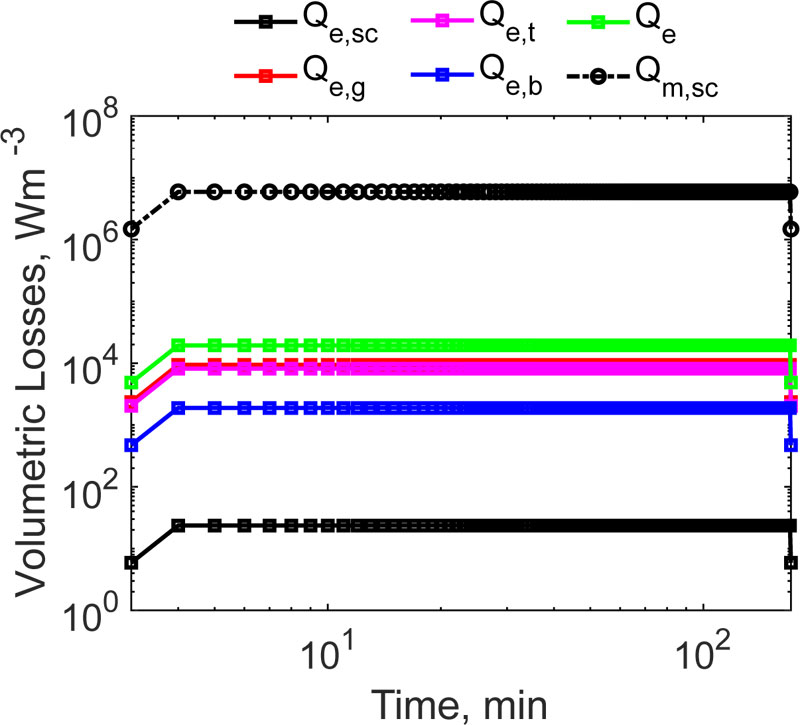
For the geometry shown in Fig. (2), a magnetic field with a strength of 12 kAm -1, working at the frequency of 300 kHz, as used earlier [27], was assumed to be applied to heat the system. The volumetric heat dissipation, due to the exposure to the RF EM field, can be distinguished in two contributions, according to Eq. (3). It is interesting to quantify which mechanism dominates, i.e. whether the dielectric losses or the power which is dissipated by the MNPs which are embedded in the implant, prevails in the heating during the HT. As a result, Qm >> Qe and QEM ~ Qm were obtained. This physical condition is due to two main reasons, namely, as usual, the induced electric field is one order of magnitude lower than the amplitude of the applied magnetic field [7], and to the huge amount of heat which is dissipated by the MNPs contained in the implant. It was demonstrated that this kind of material can produce a power per volume unit of about 10 6 Wm -3 [17], which is comparable to the calculated average value of ~6·10 6 Wm -3. Knowing the total electromagnetic power, the final outcome of the HT strongly depends on the blood tissue perfusion, as previously discussed in Sect. 2. For the magnetic implant, to produce any thermal effect, it is necessary that |QEM| > |ρbCp,bωbΔT|, taking into account that in the Pennes’ equation, the perfusion acts as a sink term (hence ΔT < 0). As can be noticed from Tab. 3.3, at the starting temperature, the power per unit volume, which is subtracted by the vascular beds of the tissues, ranges from 664 Wm -3, for the healthy bone, to a maximum of 1·10 6 Wm -3, for the tumoural region, respectively. It is worth noting that, at the initial time and temperature, the EM power, which is stored and dissipated in the target area, is higher than the energy per time and volume unit, which is removed by the system volume. At this point, a successful treatment is expected. However, the perfusion contribution in Eq. (2) is not constant. We accounted for this rather complex physiopathological condition in our simulations with Eq.s (14) and (15). Therefore, according to Eq. (15), when the temperature in the tumour volume reaches 42 °C, the perfusion doubles its value (up to 1.2 s -1), further limiting the thermal therapy. In order to assess the effectiveness of the considered magnetic hydroxyapatite thermo-seed, the spatio-temporal evolution of the system in Fig. (3) must be investigated.
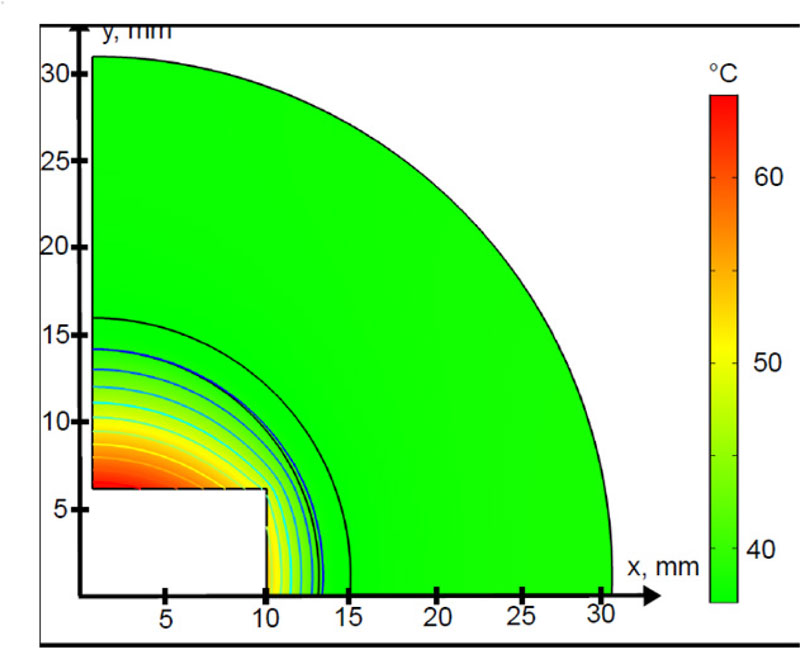
In Fig. (5) the 2D temperature profile at t=80 min is shown. The highest temperature values were found along the direction of the applied magnetic field. The power, dissipated by the MNPs embedded in the biomaterials, quickly diffuses to the surrounding fracture gap. This is due to the relatively high thermal conductivity of the hydroxyapatite material, with respect to the biological materials, as reported in Table. 3. However, the radial heating pattern presents a sudden decrease of about 3 mm away from the implant surface, tending to become homogeneous for distances higher than 20 mm. This trend resembles, from a qualitative point of view, the steady-state temperature profile, which is prescribed by Eq. (4) [10].
| ρ (kg·m -3) | k (Wm -1K -1) | C p (Jkg -1K -1) | Q M (Wm -3) | ωb (s -1) | |
| Mangetic Hydroxyapatite | 3100 | 1.3 | 700 | - | - |
| Surgical gap | 1115 | 0.6 | 2450 | 5300 | 7·10 -3 |
| Tumour | 1910 | 0.32 | 1313 | 57240 | 0.6 |
| Bone | 1900 | 0.32 | 1313 | 286.2 | 0.175·10 -3 |
| Blood | 1050 | - | 3617 | - | - |
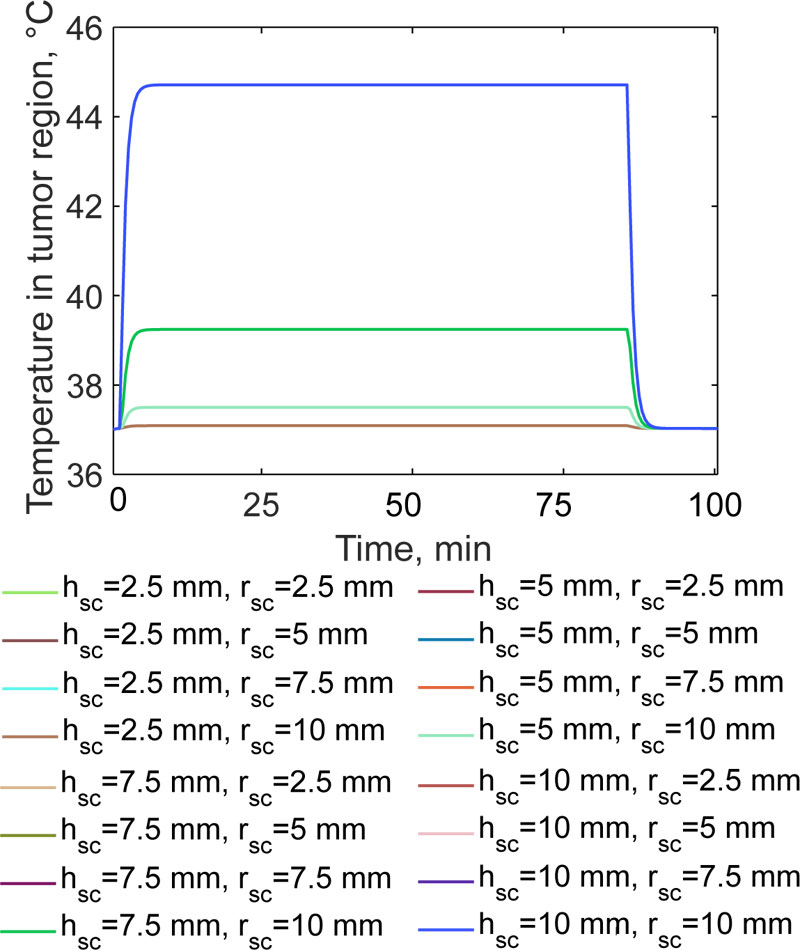
From Fig. (6) it can be noticed that the size of the implant strongly affects the average temperature in the tumour region. The quasi-steady state temperature is achieved after 13 min for each of the considered cases. For h sc=2.5 mm, the temperature is about 37.1 °C for any radius value of the implant. When the height is doubled, the temperature of the residual cells increases only up to 37.5 °C, with a very slight dependence on the radius (i.e. a variation of about 0.5 °C). When the magnetic cylinder has a height of 7.5 mm, the temperature increases to 39.24 °C ± 0.3 °C. Finally, if h sc=10 mm, the temperature in the target region is 44.71 °C, i.e. over the therapeutic threshold value of 42 °C for neoplastic cells. Such temperature level, which is maintained for 90 minutes, according to the literature, is sufficient to initiate the cascade of biological events, which could enhance the effectiveness of chemotherapy and radiotherapy [35, 36]. The average heating rates are similar to those found in previous studies [11, 14-17], but, from a quantitative point of view, are consistent with the experimental results found in other studies [26, 27]. Indeed, the magnetic hydroxyapatite implant, with properties reported
in Tab. 3.2, which was considered a case-study in this work, could reach 40 °C in 1 min of heating when exposed to the same magnetic field in a saline solution [28]. Regarding the relatively poor influence of the implant radius on the final temperature in the tumour, it must be pointed out that the external magnetic field is assumed to be applied along the y-axis of the system shown in Fig. (2), therefore, a preferred direction for the heat diffusion exists. These findings are corroborated by the temperature distribution shown in Fig. (5). Then, from the findings of Fig. (6), it is possible to infer that the design and the choice of the exposure parameters are crucial for the quality of the treatment. Therefore, the induction heating system should be designed, considering that the implant geometry strongly affects the conveyed energy and the heat transfer to the tumour region.
For all of the tested implant sizes, the temperature in the non-target tissues, the average temperature in the surgical gap and in the healthy bone is of about 39.82 °C and 37.25 °C, respectively. Despite the moderately high power, which is generated by the induced currents due to the induced electric field (see Fig. 7), the action of the magnetic implant is limited and local. The most relevant aspect is that the bone tissue is not harmed by the thermal therapy, thus ensuring possible healing of the injured body region.
However, the findings shown in Fig. (5) are not sufficient to complete the quantitative description of the quality of the hyperthermia treatment of bone tumours performed using magnetic thermo-seeds. By using the derived temperature data, the equivalent thermal dose at 43 °C was calculated using Eq. (17). The curves for the delivered therapeutic heat are shown in Fig. (8). For magnetic implants having a height of h sc < 7.5 mm, for any given radius value, r sc, the CEM43 is equal to zero, according to Eq. 17.
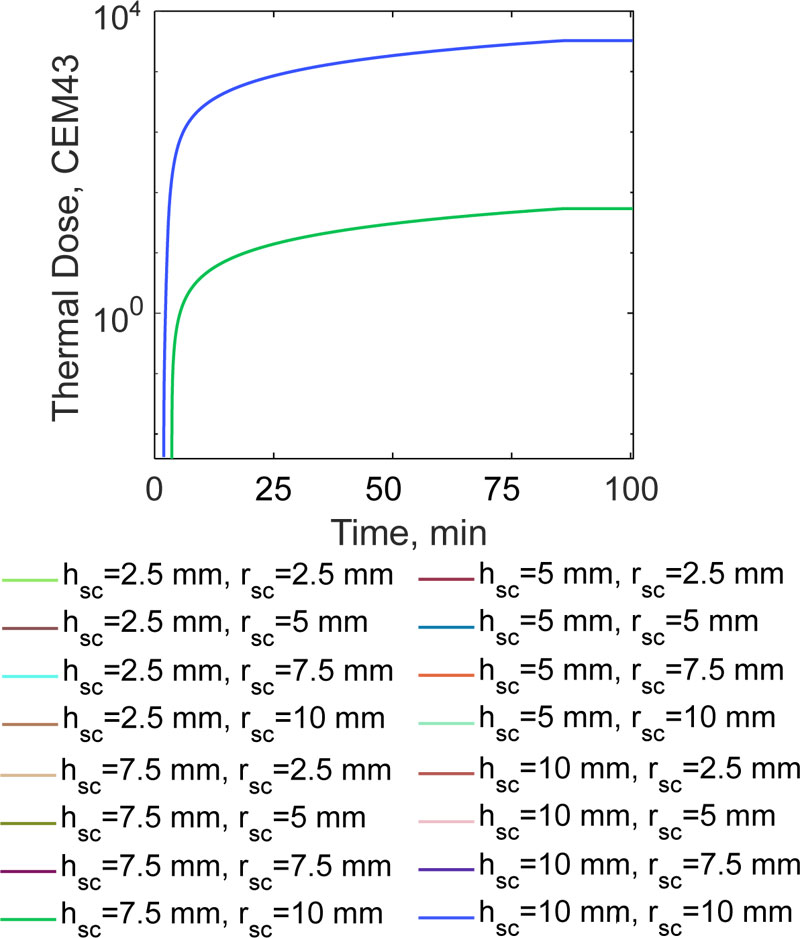
When the prosthesis height increases to 2.5 mm, coherent with the findings reported earlier (5), the CEM43 is 54.25. This value is one order of magnitude lower than the thermal dose which would be required to have the minimum biological effect [37, 38]. The highest CEM43 values, equal to 3257, for tumour tissues, were obtained when h sc= 10 mm. The range of this clinically relevant figure of merit is consistent with the previous findings reported [17, 38, 39] (i.e. from several hundred to several thousand for similar exposure times). Thanks to the proposed non-linear temperature modeling of the hyperthermia treatment, in order to treat a 0.5 mm thick region of residual bone tumour cells, it was found that the bigger the implant, the more effective the treatment.
6. DISCUSSION
This work addressed the problem of establishing a quantitative basis to simulate the hyperthermia treatment of bone tumours using magnetic thermo-seeds, taking into account the non-linear and multiphysics nature of the heat delivery and transfer during this oncologic thermal treatment. The proposed model overcomes the limitations of the available theoretical frameworks [10, 20] by providing a modified numerical resolution scheme for the coupled electromagnetic-heat transfer phenomena when both the EM and thermal properties are dependent on the system temperature. In particular, different from the model shown in a previous study [11, 14-17],the description of the magnetic properties of the implant, which determine the heat losses during the exposure to the RF field, is simplified to lower the computational burden of the numerical experiments. Furthermore, this work investigated the relevancy of the implant geometry to the effectiveness of the hyperthermia treatment.
CONCLUSION
Among the clinical advantages of the interstitial hyperthermia treatment, there is the possibility to prevent the limb amputation, thanks to the local control of the tumour recurrence, due to the improvement of the radio- and chemotherapy effectiveness, and to the possibility of operating a guided tissue regeneration. However, despite these benefits, the translation of the thermo-seeds to the clinical practice raises some issues. At first, the studied interstitial hypertermia treatment with magnetic scaffolds requires an invasive and complicated thermometry, as prescribed by the guidelines [4, 23]. Considering that potential infections and the temperature sampling would be limiting factors, it is crucial to develop non-invasive alternative methodologies for the treatment monitoring, such as magnetic resonance imaging or thermoacoustic probing with ultrasounds [37, 38]. Moreover, the long-term biocompatibility, and the possible inflammatory effects, are fundamental issues to be investigated for increasing the quality of the treatment from the biological and clinical point of views [4, 5, 34, 40-42].
Future works could investigate the crucial role of blood tissue perfusion in conditioning the outcome of the hyperthermia treatment [43-45]. The proposed non-linear model could also be used to develop a control strategy to optimize the treatment [46].
LIST OF ABBREVIATIONS
| EM | = Electromagnetic |
| FEM | = Finite Element Method |
| FS | = Fibrosarcoma |
| HT | = Hypertermia Treatment |
| MF | = Magnetic Field |
| MHT | = Magnetic Hyperthermia Treatment |
| MNPs | = Magnetic Nanoparticles |
| OS | = Osteosarcoma |
| US | = Ultrasound |
CONSENT FOR PUBLICATION
Not applicable.
AVAILABILITY OF DATA AND MATERIALS
Not applicable.
FUNDING
None.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
The authors would like to thank Mr. Matteo Bruno Lodi, Dr. Alessandro Fanti and Prof. Giuseppe Mazzarella for the help with the COMSOL model and acknowledge them for the discussion, which helped to improve this work.


