It is simple to apply and use the conventional CDY model, a system of three ordinary differential equations (ODEs), to better understand the grape production prediction over time, including any potential climatic effects. A dynamic system is created by three connected ordinary differential equations that describe the temporal evolution of the next three components:

1. The climatic effect, C(t): These are the vineyards that are not now contaminated, but might be. Vineyards that are vulnerable may get the disease or continue to be vulnerable.

2. Disease, D(t): These are the vineyards that have already contracted the disease due to the climate and can spread it to vineyards that are vulnerable. A sick grapevine may continue to grow on the infected plant or it may be removed and allowed to heal or perish.

3. Yield Y (t): These are the vineyards that are believed to have recovered from the illness.

The CDY model, which is based on these presumptions and ideas, uses the following system of ODEs, to control the rates of change in the three equations.

Assuming that the developing factors include temperature, relative humidity, rainfall, and the yield forecast model, wet days will all be regarded as climatic domain characteristics. Downy mildew disease and yield are denoted by D and  Y. The schematic diagram for the agro-climatic disease grape yield model's real-life theoretical results is presented in Fig. (1).

Fig. (1). Schematic diagram for CDY model.

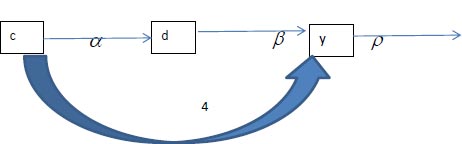
The domain's metrics include the incidence of diseases, the rate of infection, and the pace at which harvest season yield loss is eliminated. It is taken into account when creating the asymptotic analysis-based model for predicting grape yield in an agro-climatic environment. The model's fundamental structure is shown below [27]:

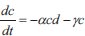(1)

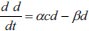(2)

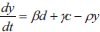(3)

Thus, the starting conditions are

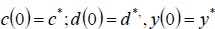(4)

Using the asymptotic method to solve equations (1-3), where c is the climatic effect, d is the downy mildew disease, y is the yield, t is the time in days, α αis the infection rate for grapes, β is the disease incidence rate for grapes, γ is the seasonality rate, and ρ is the removal rate of grape yield loss per harvest time, we can obtain the following:

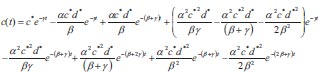(5)

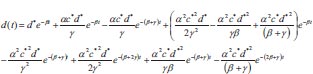(6)

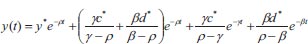(7)

An equilibrium point is a location where a system's variables are steady throughout time. The equilibrium 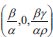can be found in equations (1)–(3), and this equilibrium point is a stable one for the system. A system will gradually return to its steady state if it is in a stable steady state and is only slightly perturbed from the steady state.

As a result, little variations in crop production will not upset the balance. This equilibrium should be seen in the natural world. In this approach, conduct that is physically viable is often determined by stability. It is established that equations (1) through (3) behave in a linearized fashion at equilibrium. To evaluate this, a Jacobian matrix is required [27].

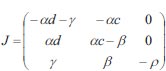At an equilibrium point

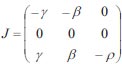Eigenvalues of the Jacobian matrix are λ₁ = 0,λ₂ = -ρ,λ₃ = -γ

In the system, Re(λ_i)< 0, so the given system is stable. It is clear to see that the system (1)-(3) has disease-free equilibrium 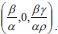. Let X = (c,d,y)^T, then the system (1)-(3) can be written as X = F(X) - V(X).

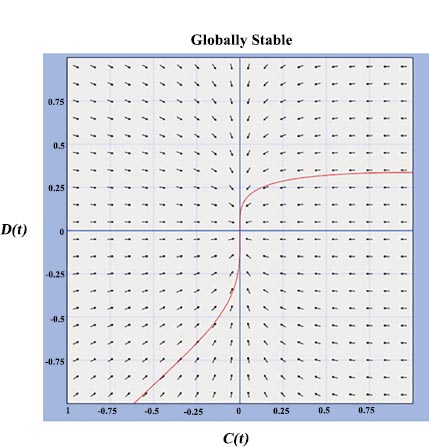
Fig. (2) shows a direction field numerical analysis of stability.

Thus, if R ₀ = spectrum(FV^-1), the system in question is globally stable. It studies the dynamic behaviour and develops a yield forecast model. Moreover, it bears the fundamental reproduction number, R ₀, which plays a crucial role. The disease-free equilibrium is reached, when the fundamental reproduction number is less than or equal to one, where disease finally dies out, demonstrating the global stability of the equilibria. Fig. (3) makes it clear that both the upper and lower positive states as well as the globally stable state are stable nodes. It is clear that the CDY model for grapes is more accurate at predicting yield and is globally stable in the disease-free equilibrium.

Fig. (2). An illustration of the climatic disease yield forecast system's phase plane. The phase fluxes of matter across the system are depicted by arrows.

Fig. (3). Site map for muscat hamburg grape cultivation. structural view of the grape model using the android app.

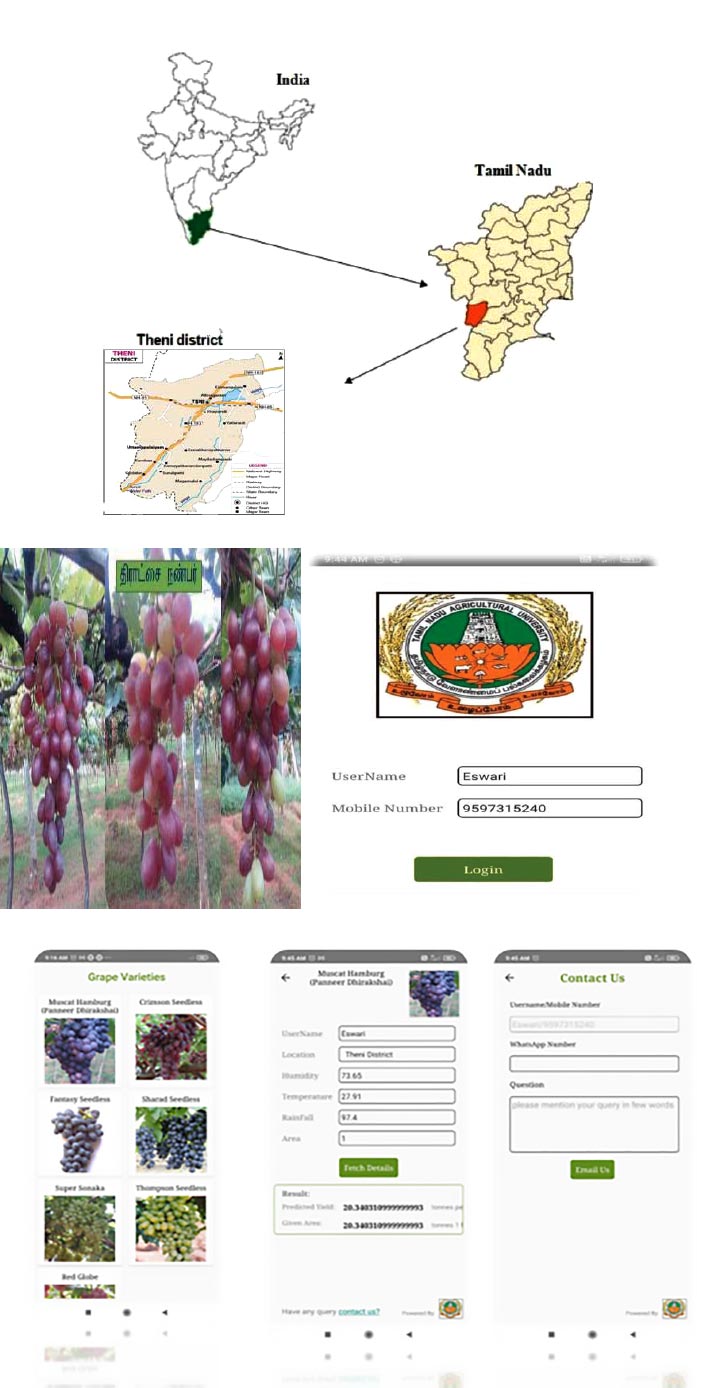
Due to their compatibility with farming's inherent mobility, low cost, and ability to produce a wide range of useful applications, Android apps have become an important tool in agriculture. Additionally, modern Android apps come with a variety of physical sensors, making them a viable tool for assisting with a range of farming duties. Applications for Android phones that fall under the agricultural category help farmers cultivate crops by monitoring their surroundings with a variety of sensors. Photographs taken at certain farm places, and notes made on the colours of the soil, water, plant leaves, and light can all be considered observations. The application's primary target users frequently work to increase farm output by examining agricultural samples, assisting with agricultural decisions and resolving task-specific issues. The data on yield, intensity of diseases, weather data on temperature, rainfall (intensity and frequency), and humidity, from 2016 to 2021, were collected from the Theni district. The developed mathematical model for yield prediction and disease forecasting under different climatic conditions in the sample area was validated using an Android app. The created model was used to assess the decline in grape output. Using this suggested model, decisions could be made to help farmers produce more grapes. The developed mobile app will be helpful for grape farmers to avoid unnecessary applications. It can be used to control disease outbreaks in grapevines. It predicts the growth and fruit development pattern of grapes. The current study was carried out to create an Android app, taking into account the aforementioned data, and validate a mathematical model for grapes with regards to climate conditions and disease incidence.

This app is a farmer-friendly app; it is easy to download this app on mobile or laptop. After downloading, the login page of this app can be opened and the username and password can be entered to login into it. In this app, the varieties of grapes are pictorially shown from the Grape research station, Theni district. Any one variety can be clicked to open the input details page related to climatic factors, such as temperature, relative humidity, and rainfall within the area. All such inputs are provided to estimate an output for grape yield prediction. Using this app, every farmer can estimate grape yield for future perspective.

The study has been conducted on established grapes vineyards with Muscat Hamburg variety in a plot size of 30 x 6 m2 (30 vines). The experiment plot involved 30 vines, which were maintained without fungicide sprays during the growing season so as to observe the development of downy mildew disease. To identify the oil spot symptom, the third or fourth leaf in a vine was marked separately using a label, and thus, a total of 75 leaves were marked per replication. The occurrence of the symptom as the oil spot was considered further for observing disease development for scoring at the scale of 1-9 and calculation of the percent disease index [14, 15].

We have surveyed the grapes growing areas to assess the incidence of downy mildew from 2016 to 2021. The disease incidence was assessed using data collected from the grapes vineyards located in the Cumbum, Chinnamanur, and Uthamapalayam blocks of the Theni district. For the purpose of gathering data on disease incidence levels, 15 vineyards have been chosen. From the chosen vineyards, observations on the disease incidence have been gathered twice weekly. The results of the survey have demonstrated downy mildew as a serious illness compared to other infections. Downy mildew has also been found to be a significant illness, particularly 0–60 days following forward (fruit) trimming. Between 2016 and 2021, the prevalence and severity of downy mildew disease at the field level have been evaluated. Using the field-level data, the proposed model could be validated, and the results are presented in Fig. (4). The rate of crop loss per harvest time, illness incidence, infection rate, and seasonality index are the new analytical representations of climate, disease, and yield, as shown in Eqs. (5-7). The fluctuating relative frequencies of infection, illness severity, and practical seasonality all have an impact. Field-level data were compared with that of the agro-climatic grape yield model and the numerical findings, the infection rate, seasonality index, and disease severity have been taken into account with respect to the time in days, as shown in Fig. (4). The chart shows that when the disease automatically increases, climate rises, and other yields initially become zero. However, after a long period, the climate declines, with increasing production, inducing a natural decline in the disease.

Fig. (4). Time in days for c* = 33,d* = 0,y* = 0,α = 23.98,β = 24.04, γ = 90, ρ = 0.2. The solid line and dotted line show the analytical and numerical results, respectively. Fig. (5) shows the plot of seasonality indices versus time in days for grapes under the influence of climatic elements, like the highest and lowest temperatures, relative humidity, and rainfall in the Theni district during the years 2016-2021. The highest seasonal index for maximum temperature has been noticed in April (1.13%), followed by May (1.09%) and March (1.08%). A seasonal index of 1.13 indicated that the season had 13% more than the seasonal average of maximum temperature in April. The lowest seasonal index for maximum temperature was noticed in December (0.93%), followed by January (0.93%) and August (0.95%). A seasonal index of 1.13 indicated that the season had 0.02% less than the seasonal average of maximum temperature in December. Similarly, all the weather indices can be interpreted in the below format.

Fig. (5). Seasonality indices versus time in days for grapes under the influence of climatic factors. a. Max. temperature, b. Min. temperature, c. Relative humidity, and d. Rainfall in the Theni district during the years 2016-2021.

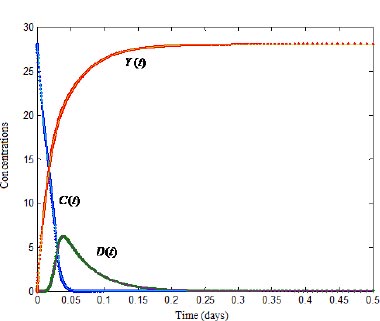
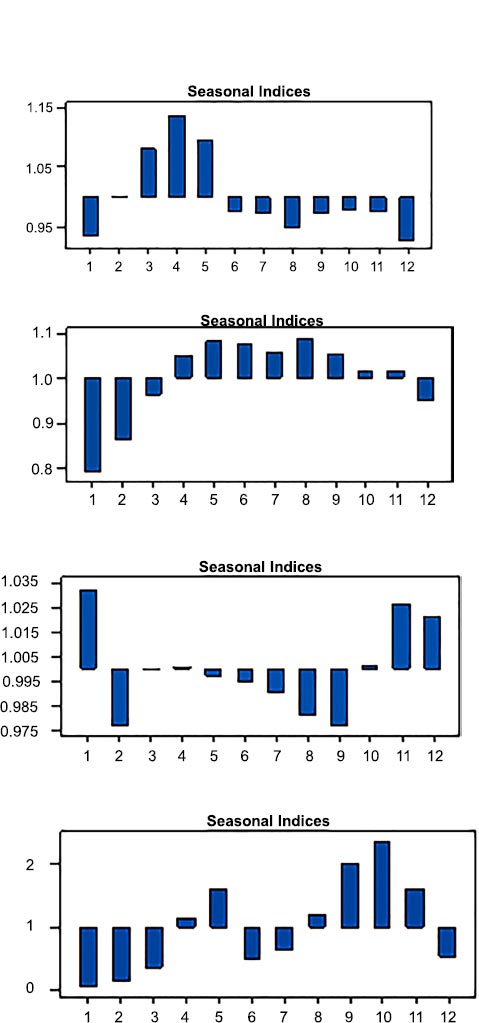
Fig. (6) depicts the three-dimensional spatial distribution of the climate for varied effective seasonality and infection rates. The climate is self-governing of both α and γ; nevertheless, C^* diminishes the climatic effect.

Fig. (6). The relationship between disease incidence β and climatic effect for different effective seasonality rates and infection rates; c* = 33, d* = 0,y* = 0.

Fig. (7). Influence of the effective seasonality rate on disease for variable infection rates and disease incidence; c* = 33, d* = 0,y* = 0.

Fig. (8). Influence on the infection rate of the yield with respect to varying effective seasonality rates and disease incidence; c* = 33, d* = 0,ρ* = 0.2.

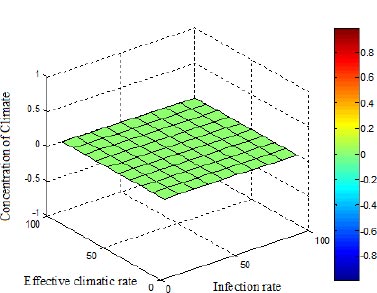
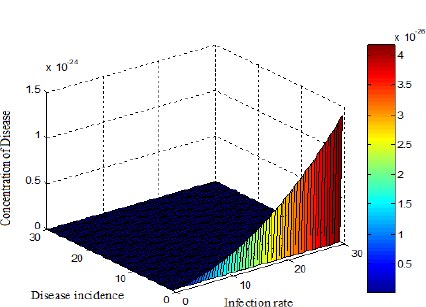
According to Fig. (7), the disease varies for high values of the infection rate and disease incidence. In this system, the disease rises as the rate of infection rises, when β < 10.

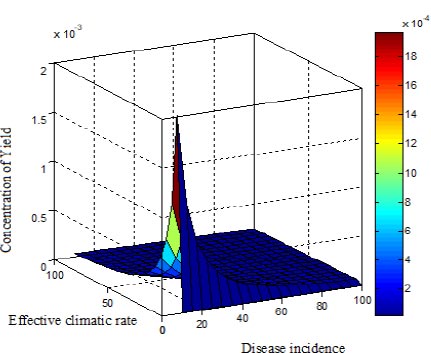
Regardless, when the yield is in a constant quantity, the sickness incidence is quite high, as shown in Fig. (8).

We can infer that when both the seasonality index and disease incidence marginally decline, the yield rises. Table 2 compares simulation findings with analytical expressions of climate, illness, and yield. In the created model, the analytical solution contributed to 0.2832%, and numerical simulations have obtained the maximum relative error. The generated model has also been subjected to a parametric Jacobian transformation stability study. It is advised to utilise the created model (Eq. 5-7) to calculate the yield of the grapes based on the results of the mathematical experiments that have been conducted. Furthermore, the algebraic approach can be used to forecast or consider both linear and non-linear systems.