The Analytical Scheme on the Inertial Drag for Buoyancy-driven Nanofluid Flow Under Convective Thermal Surface with the Soret Effect
Abstract
Introduction:
The two-dimensional mixed convection of nanofluid over a vertical expanding surface is analysed in the current discussion. The expanding surface is embedded in a permeable medium.
Methods:
In advance, Darcy Forchheimer inertial drag is considered along with the influence of Brownian and thermophoresis, which enriches the study. The novelty of the study is due to the mass concentration along with the role of volume concentration in the flow phenomena. The proposed model is designed in association with a characterizing parameter, which is attained by the use of appropriate similarity conversion. Further, the system of first-order differential equations is resolved by employing a shooting-based numerical method, in particular, the Runge-Kutta fourth-order technique.
Results:
The simulated results for the said parameters and their behaviour are deployed through graphs and in tabular form.
Conclusion:
The physical description of each parameter is deliberated briefly. Finally, the important outcomes of the proposed study reported a remarkable hike in the temperature profile that is observed for the enhanced thermophoresis and Brownian motion. Further, the shear rate also increases for the enhanced mixed convection parameter.
1. INTRODUCTION
Soret effect or thermophoresis is nothing but the phenomenon of showing numerous responses to the force of a temperature gradient by different particles of a mixture. It has different applications in practical situations like the separation or mixing of particles and differentiation of the impure ions in a chemical process, and it is also used as commercial precipitators. This phenomenon of gaseous mixtures was first introduced by John Tyndall, and later it was described by John Strutt. Similarly, mixed convection is a process that occurs when natural convection and forced convections combine together in a mechanism to transfer heat. In some cases where forced convection is not efficient, at that time, mixed convection gives better results. The process is used in various fields, such as in nuclear reactor technology, some electronic cooling processes, etc. Again, the convective boundary condition is also known as the Newton boundary condition. Many researchers have given many results on mixed convection flow, the Soret effect and convective boundary conditions.
Eringen [1] is the pioneer of micropolar fluid, which is nothing but the motion within the locality and the transformations of the primitive fluid elements. Recently, nanomaterials have been often used to upgrade the thermal conduction of base fluids in mechanical engineering, nanotechnology, bioscience, etc. The submerging of these nano-meter sized particles in a base liquid is called nanofluid. The word nanofluid was termed by Choi [2] over a decade ago. RamReddy et al. [3] deliberated the variation in heat and mass transport with respect to the Soret effect under convective conditions, and the numerical approximations are found by employing the finite difference method. Bourantas and Loukopoulos [4] reported a micropolar-based nanofluid model. The significance of this model is that it considers the microrotation and natural convection of nanoparticles. Rashidi et al. [5] explore the magnetohydrodynamic (MHD) stagnation point flow of a micropolar nanofluid between parallel porous plates with uniform blowing. The study investigates the fluid dynamics and heat transfer characteristics of this complex system, shedding light on its behavior through numerical analysis. The research contributes to the understanding of nanofluid behavior in porous media under the influence of magnetic fields and external blowing. Hsiao [6] studied the influence of magnetic field and viscous dissipation on micropolar nanofluid flow over a stretching sheet. The research explores the dynamics of this complex system, incorporating multimedia elements to enhance comprehension. The findings contribute to the understanding of nanofluid behavior in the presence of multiple physical effects. Hayat et al. [7] investigated the mutual significance of Brownian motion along with thermophoresis in micro-structured nanofluid across enlarging surface. The effects of thermal radiative effect, Newtonian heating along with Brownian motion parameter are also analyzed in their survey. Alizadeh et al. [8] surveyed the transmission of heat in hydromagnetic micropolar nanofluid under the influence of thermal radiation and other diverse parameters like micropolar parameters, magnetic parameters etc. An electrically conducting micropolar fluid's properties of double-diffusive heat and mass transmission, as well as convective circumstances and chemical reaction, were studied by Pal and Biswas [9] on a nonconstant plate. Siddiq et al. [10] studied the magnetohydrodynamic (MHD) stagnation point flow of micro-structured nanofluid along a contracting sheet and the impact of thermophoretic and Brownian motion parameters on the fluid. The numerical results are approximated by RKF45 Runge-Kutta-Fehlberg (RKF45) method and different physical parameters are presented in graphs as well as tabular form. Lund et al. [11] investigated the behavior of a micropolar nanofluid under the influence of magnetohydrodynamic flow and buoyancy effects. The study focuses on a vertical shrinking surface and explores the existence of dual solutions. They provide a mathematical analysis of the complex fluid dynamics involved in this scenario. The findings contribute to a deeper understanding of MHD flow and its applications in nanofluid dynamics. Patel and Singh [12] reported the combined effects of thermophoresis, Brownian motion, and nonlinear thermal radiation on mixed convection MHD (magnetohydrodynamic) micropolar fluid flow. The study focuses on a nonlinear stretched sheet placed in a porous medium with additional considerations such as viscous dissipation, Joule heating, and convective boundary conditions. The research investigates the impact of these factors on heat and mass transfer within the system. Nadeem et al. [13] investigated a three-dimensional unsteady flow of incompressible micropolar nano-structured fluid with the occurrence of microorganisms via an exponentially extended sheet, which are mostly applicable in microbial fuel cells. Bilal [14] addressed the mass and heat transport of an MHD micro-type nanostructured fluid over a stretched sheet along with convective boundary situations. The Runge-Kutta (RK) integration and the shooting method, is employed to handle the numerical calculations. Tlili et al. [15] analysed the impact of bioconvective microstructure nanofluid consisting of microorganisms on thermal as well as solutal stratifications nearby the boundary. Also, the study takes into account partial slip and double stratification effects. The research focuses on the numerical analysis of the flow behavior and heat transfer characteristics. The study provides valuable insights into the influence of gyrotaxis, partial slip, and double stratification on the flow dynamics and thermal properties of the nanofluid. Zadeh et al. [16] deliberated the mass and heat transport of micropolar non-Newtonian nano liquid with the impact of motile microorganisms on a widening sheet. Ali et al. [17] delve into finite element simulation of bioconvection and Cattaneo-Christov effects impacting micropolar-based nanofluid flow over a vertically stretching sheet. They have examined these phenomena through rigorous analysis, contributing to the understanding of complex fluid dynamics. The research sheds light on the interplay between various factors, offering insights into nanofluid behavior with potential implications for diverse applications. Izadi et al. [18] investigated magnetohydrodynamic (MHD) thermo-gravitational convection and thermal radiation in a porous chamber filled with a micropolar nanoliquid. Their work displays the interplay of MHD effects and thermal radiation on the convective heat transfer characteristics of the nanoliquid. Kumar et al. [19] used the Galerkin method to solve the governing equations for the research on unsteady magnetohydrodynamic (MHD) natural convective flow under the effect of Hall current, Radiation, Soret and Dufour effect. Song et al. [20] studied the nonlinear thermally radiative heat transport in a Brinkman-type micropolar nano-material over an inclined surface. The analysis considers the presence of motile microorganisms and an exponential heat source. The researchers employ mathematical modeling and numerical techniques to analyze the heat transfer characteristics. The results contribute to understanding heat transport phenomena in complex systems involving microorganisms and nano-materials. The findings provide valuable insights for applications in various fields, such as biotechnology and materials science. Ahmad et al. [21] investigated the convective heat and mass transfer magnetohydrodynamic (MHD) micropolar fluid over a slant surface with effect of wall suction, magnetic, shear stress, and viscus dissipation along with some other parameters. The mutual consequence of the Soret as well as Dufour on convective heat and mass transport for the flow of an irregular boundary layer across a vertical channel with the involvement dissipation and constant suction were explored by Ahammad and Krishna [22] and used Crank-Nicolson scheme to handle the governing equations.
Khan et al. [23] addressed the dual diffusion heat mechanism of nanomaterials under the action of thermal radiation and temperature absorption/production. In order to discover the analytical expressions, the Homotopy analysis approach is enforced. Khan et al. [24] studied micropolar nanofluid in three dimensions along with the impact of thermal radiation, activation energy and magnetic effects. Song et al. [25] identified the features of activation energy along with the thermal radiation in micropolar nanofluid with motile microorganisms through a stretched sheet. Waqas et al. [26] analysed the bio-convection transport of micropolar-based nanomaterials and gyrotactic motile microorganisms’ consequence with thermal radiation and activation energy past a needle moving in parallel flow. Pattnaik et al. [27] explored the impression of the shape of nanoparticles on the conducting nano-structured fluids via a porous matrix. Afzal et al. [28] studied the nanoparticles in the stream of general micropolar fluid along with Carreau fluid across a flat surface. El-Dawy and Gorla [29] examined a steady laminar flow of microstructured nanofluid via an extended and contracting wedge with the effect of heat production or preoccupation and an induced magnetized field across a wedge surface.
Salmi et al. [30] inspected the impression of motile organisms in microstructure fluid in the context of simultaneous thermal and mass transmission along with thermal diffusion. Baag et al. [31] explored the behaviour of radiant heat on a moment flow of MHD microstructure fluid towards upward overextended sheet with the collaboration of a transverse magnetic field along with the Soret effect and convective conditions. Khan et al. [32] analysed the buoyancy impact on moment flow caused by a hybridized microstructure nanofluid across a porous plate. Hussain and Xu [33] reported a non-Newtonian magnetohydrodynamic (MHD) micropolar fluid in which the nanofluid theory is implemented to discuss the thermophoresis and the Brownian motion phenomenon along with bioconvection and buoyancy forces. Barik et al. [34] investigated the circulation of hydromagnetic nanostructured fluid, including the consequences of a slippery situation responding to an elastic interface. Additionally, Mishra et al. [35] have published the influence of nonlinearly radiated via an elongating interface employing mutual diffusion as well as magnetic heat flux efficiency. The Adomian decomposition method was used to model thermal energy transmission in the nanofluid over a semi-infinite straight sheet by a porous media analyzed by Mishra et al. [36]. Pattnaik et al. [37] implemented the technique developed by Runge-Kutta with a shooting approach to examine two-dimensional magnetohydrodynamic (MHD) flow in a nano-structured fluid together with the implications of different physical variables. In a recent study, Krzywanski [38] explores improved heat transfer performance in an industrial circulating fluidized bed combustion (CFBC) system by using fuzzy logic-based techniques. In another work, Krzywanski et al. [39] investigated an AI-based approach to predict heat and mass transfer in fluidized beds, offering potential insights into cooling and desalination processes.
The earlier investigations presented through the aforesaid literature show that not much work on the case of assisting/opposing has been conducted for the flow of nanofluid. Therefore, the mixed convection effect with assisting/opposing is deployed for the flow of nano-structured fluid with the implication of Darcy-Forchheimer inertial drag along with thermal radiation. The objective of the study is to develop an analytical framework for understanding and predicting the inertial drag in buoyancy-driven nanofluid flow. The study specifically focuses on nanofluids subjected to convective thermal surface conditions and considers the influence of the Soret effect. By establishing an analytical scheme, the researchers aim to provide insights into the complex interplay between fluid flow, heat transfer, and nanoparticle migration in such systems. The developed framework can contribute to the design and optimization of nanofluid-based technologies with enhanced thermal performance.
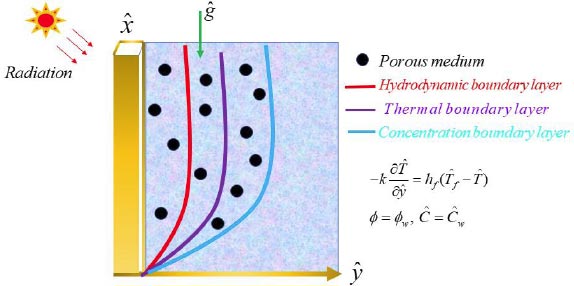
2. MATERIAL AND METHOD
A two-dimensional coordinate system is contemplated in which the y-axis is perpendicular to the x-axis and flows towards the horizontal direction. A continuous mixed convective heat and mass transmission are considered via a vertical and flat sheet that is implanted in a nano-structured fluid consuming
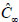 (concentration)
(concentration)
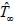 (temperature) and φ∞ (nanoparticle volume fraction) in the ambient medium. Also, a free stream with steady velocity
(temperature) and φ∞ (nanoparticle volume fraction) in the ambient medium. Also, a free stream with steady velocity
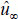 passes via a flat plate is considered (Fig. 1).
passes via a flat plate is considered (Fig. 1).
•
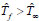 agreeing to assis flow i.e., heated surface and
agreeing to assis flow i.e., heated surface and
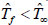 agreeing to oppose flow i.e., cooled interface.
agreeing to oppose flow i.e., cooled interface.
• The fluid viscosity and the volume of the nanoparticles on the wall are reserved to be fixed and are specified by
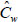 and Øw correspondingly.
and Øw correspondingly.
The leading equations derived by using the Oberbeck-Boussinesq approximation, using the conventional boundary layer approximation and removing pressure are given by:
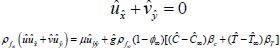 |
(1) |
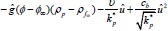 |
(2) |
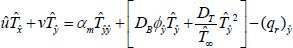 |
(3) |
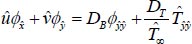 |
(4) |
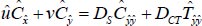 |
(5) |
As well as boundary restrictions:
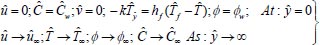 |
(6) |
Where ѱ function is given by:
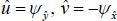 |
(7) |
And let us take the following non-dimensional transformations:
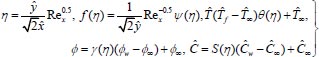 |
(8) |
Now substituting equation (7) from equations (2) to (5) and then using the above transformations, we have;
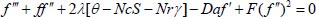 |
(9) |
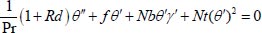 |
(10) |
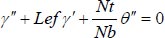 |
(11) |
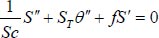 |
(12) |
Here, the prime notations indicate the differentiation with respect to η. Also, the conditions in (6) in terms of ƒ, θ, γ, S reduce to:
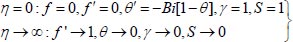 |
(13) |
The interesting and important aspects of the shear rate Cƒ and heat transfer rate Nu are presented as,
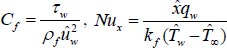 |
(14) |
Here, τw is skin friction, qw is heat flux at the surface is:
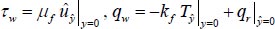 |
(15) |
yields to
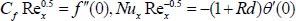 |
(16) |
Here,
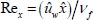 , Reynold’s number is presented locally.
, Reynold’s number is presented locally.
3. NUMERICAL METHODOLOGY
3.1. Adomian Decomposition Method (ADM)
The standard modelled equations articulated in equations (9-12) are nonlinear ODEs. Here, we have applied a semi-analytical method to solve the equations known as the Adomian Decomposition Method.
First, we introduce the operators
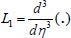 and
and
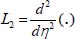 with inverse operators
with inverse operators
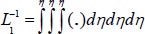 and
and
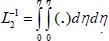 . Thus, by applying ADM, the equations (9-12) can be written as
. Thus, by applying ADM, the equations (9-12) can be written as
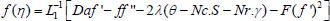 |
(17) |
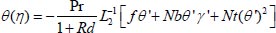 |
(18) |
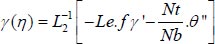 |
(19) |
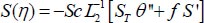 |
(20) |
ƒ(η), g(η), θ(η) and ϕ(η) can be expressed in the power series form stated as:
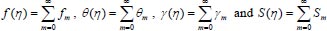 |
(21) |
For the rest terms of the equations (17-20), take the power series expansions as:
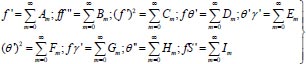 |
(22) |
From equation (13) and the assumed initial conditions are:
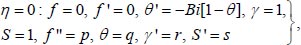 |
(23) |
where the values of p, q, r, s are to be resolute.
Applying these conditions, the initial and succeeding order solutions are articulated as:
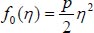 |
(24) |
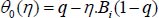 |
(25) |
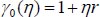 |
(26) |
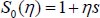 |
(27) |
And:
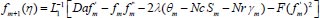 |
(28) |
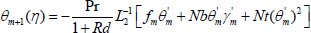 |
(29) |
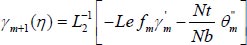 |
(30) |
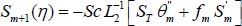 |
(31) |
Putting the values of m = 0,1.... one can obtain the solution of the governing equations as:
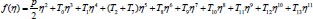 |
(32) |
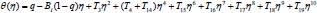 |
(33) |
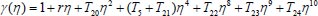 |
(34) |
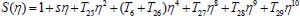 |
(35) |
However, for the sake of brevity,the values of T'is are omitted.
4. RESULTS AND DISCUSSION
The subject presents the buoyancy-driven nanofluid flow toward an extending vertical surface entrenched with a porous media. The Darcy-Forchheimer inertial drag with the effect of thermophoresis and Brownian motion enriches the study. One of the vital aspects of the present study is the inclusion of the volume concentration. The designed model for the governing modelled equations is solved by employing a semi-analytical technique followed by suitable similarity transformations that are helpful for making non-dimensional for of flow phenomena along with the surface conditions. In particular, the Adomian decomposition method is deployed for the solution of the system. The behaviour of the particular constraints is exhibited and displayed graphically. However, the simulations for CƒRex0.5 and NuRex0.5 are deployed via the tabular form. The computation involves the fixed values of the constraints, such as Da = 0.2, F = 1, Bi = 0.1, λ = 0.2, Nt = 0.3, Nb = 0.2, Nc = 0.1, Rd = 0.3, Pr = 2, Le = 1, Sc = 0.1, St = 0.1 where the standard variation of each parameter is displayed in the corresponding figures.
4.1. Description of Parametric Behaviour
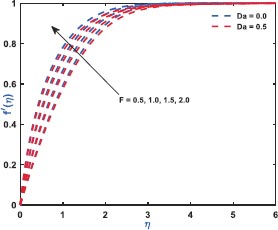
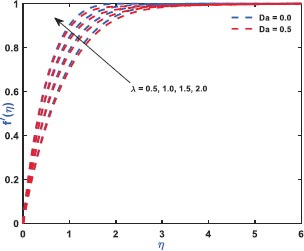
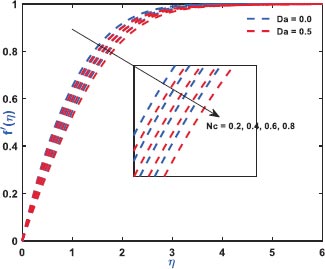
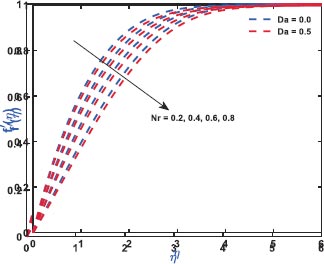
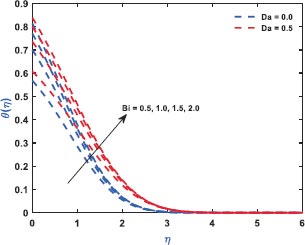
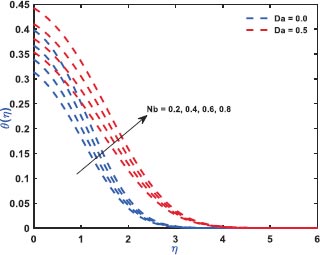
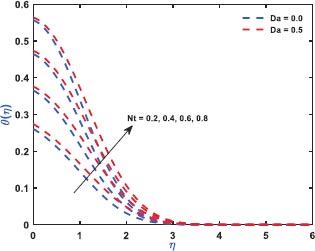
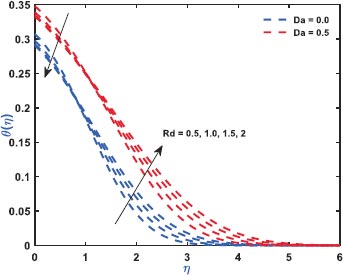
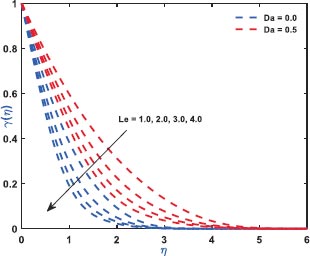
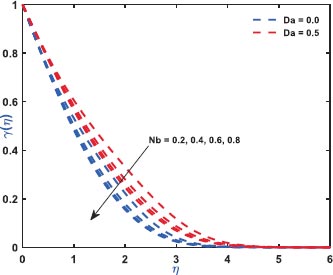
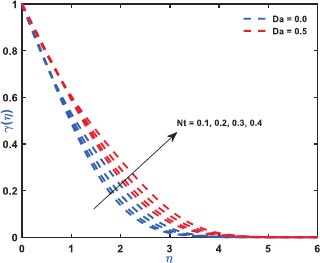
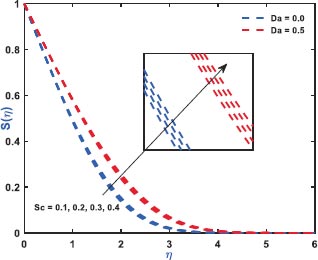
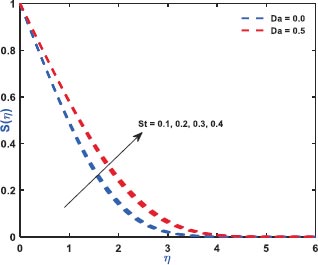
Fig. (2) exhibits the role of inertial drag due to the existence of a porous matrix on the ƒ'(η). It is the force that pushes the fluid away from the moving body that differs from viscous force. The Figure shows the variation with respect to the appearance (Da = 0.5)/non-appearance (Da = 0) of the Darcy parameter. It clarifies that enhanced drag overshoots the velocity distribution irrespective to the variation of Darcy parameter for which the thickness of the bounding surface retards significantly. Fig. (3) reveals the noteworthy features of the mixed convection parameter on the fluid velocity. The impact is due to the variation of the thermal Grashof number i.e., buoyancy factor. Buoyancy is an upward force that is observed owing to the pressure differential between the fluid layers. The top layer pressure is dominated by the bottom and the fluid at bottom moves away for which the fluid velocity enhances throughout. Fig. (4) signifies the role of regular buoyancy parameter affecting the fluid velocity for the variation of Darcy parameter. It is defined as the ratio of the concentration difference with the temperature differential between the wall and the boundary. The increasing buoyancy of the temperature difference retards so it affects the fluid velocity and therefore, the fluid velocity also decreases significantly. Fig. (5) reflects the influence of nanofluid buoyancy parameter on the fluid velocity. It is defined as the ratio of the concentration difference with respect to the temperature difference. A similar effect is rendered as previous since, the enhanced buoyancy is due to the retardation in the temperature difference vis-à-vis the concentration increases, therefore the fluid velocity attenuates gradually. The presence of permeability also attenuates ƒ'(η) greatly comparing to the impermeability of the medium. Fig. (6) elaborates the significance of Bi on the θ(η) in association with the involvements of permeability. The calculation of heat transport is conducted by the use of Bi. It is described as the thermal resistance ratio for the conduction inside the body with respect to the resistance for the convection at the upper surface. The numerical value of the Biot number less than unity shows the thermal profile is stable. The figure discloses that the enhanced Bi augments the θ(η) irrespective to the various Darcy numbers. However, increasing Darcy number enhances the temperature profile since the resistance is due to the permeability that stored near the sheet region that overshoots the profile. Fig. (7) characterizes the properties of Brownian motion θ(η). The two-layer difference within the domain demonstrates the behaviour of the Brownian motion for the effect of porosity. The increasing porosity enhances the fluid temperature, as discussed earlier, and the increasing Brownian motion also favors in augmenting the temperature profiles. Fig. (8) illustrates the role of thermophoresis that affects θ(η). It occurs due to the diffusion of the thermal gradient in γ(η) and the augmentation in the thermophoresis parameter, and the nanofluid temperature rises up for which it enhances the profile asymptotically. However, the observation reveals that the impermeability of the surface provides greater control over temperature. Fig. (9) portrays the significance of the radiating heat approaching to a linear radiative model on the fluid temperature profiles. It is used as a measure for the amount of emitted electromagnetic radiation from the fluid elements. This electromagnetic radiation is further transformed into thermal radiation. The result shows a dual behaviour within the domain. It can be seen that near the sheet region the profile was retard but with increasing domain, it shows opposite behaviour on the profile. Fig. (10) characterizes the role of the Lewis number on the profiles of volume fraction. The occurrence of Lewis number is owing to the existence of the Brownian diffusion coefficients. It is expressed as the ratio of the thermal diffusion and the Brownian diffusion. Therefore, enhancing Lewis number occurs for the decreasing Brownian diffusion and it helps to retard the volume concentration profile. Figs. (11 and 12) portray the role of the Brownian factor along with thermophoresis factor on the volume faction profiles. The behaviour shows the variation of permeability on the profiles. Here, the volume concentration attenuates for the increasing Brownian motion but the profile behaves in opposite direction for the increasing thermophoresis. The comparative analysis exhibited that the situation of permeability overrides the situation of impermeability of the medium. Fig. (13) illustrates the behaviour of the Sc affecting the nanofluid concentration distribution with the variation of porous matrix. The existence of the Schmidt number is due to the occurrence of heavier species considered in the flow phenomena. The expression of Schmidt number describes the relationship between the kinematic viscosity and the solutal diffusivity. The profile attenuates with the increasing Schmidt number therefore; the heavier species has a greater control in reducing fluid concentration. Further, Fig. (14) elaborates the experience of the Soret number on the fluid concentration. When the fluid temperature diffuses in the concentration distribution, the fact is termed as Soret. The result depicted that increasing Soret increases the concentration distribution asymptotically. Moreover, in both the figures, it is clearly visible that the flow via impermeable medium favors in controlling the fluid concentration, whereas the flow through permeable surface overshoots the profile significantly.
Finally, it is important to discuss the numerical outcomes for the simulated values of the rate coefficients such as CƒRex0.5 and NuRex-0.5. Table 1 displays the variation of diversified constraints on the profiles of shear rate. The observation discloses that for the augmentation in the regular buoyancy, the nanofluid buoyancy ratio and the Darcy number due to the permeability of the medium retards the shear rate coefficients, whereas the mixed convection parameter and the Darcy-Forchheimer inertial drag overshoots the profiles of shear rate significantly. Further, Table 2 depicts the behaviour of characteristic factors on the heat transfer rate coefficients to see the performance of the Nusselt number.
| λ | Nc | Nr | Da | F | CƒRex0.5 |
| 0.1 | 0.2 | 0.9 | 0.8 | 0.8 | 0.4232 |
| 0.2 | - | - | - | - | 0.4902 |
| 0.3 | - | - | - | - | 0.5545 |
| 0.1 | 0.2 | - | - | - | 0.4417 |
| - | 0.4 | - | - | - | 0.3431 |
| - | 0.6 | - | - | - | 0.2411 |
| - | 0.2 | 0.3 | - | - | 0.3927 |
| - | - | 0.5 | - | - | 0.2926 |
| - | - | 0.7 | - | - | 0.1882 |
| - | - | 0.9 | 0.3 | - | 0.3471 |
| - | - | - | 0.5 | - | 0.2068 |
| - | - | - | 0.7 | - | 0.1551 |
| - | - | - | 0.8 | 0.2 | 0.3562 |
| - | - | - | - | 0.4 | 0.3841 |
| - | - | - | - | 0.6 | 0.4154 |
| - | - | - | - | 0.8 | 0.4507 |
| Pr | Nb | Nt | Rd | Nu Rex-0.5 |
| 0.71 | 0.1 | 0.5 | 0.5 | 0.0884 |
| 1 | - | - | - | 0.0881 |
| 2 | - | - | - | 0.0851 |
| 0.71 | 0.1 | - | - | 0.087 |
| - | 0.2 | - | - | 0.0851 |
| - | 0.3 | - | - | 0.083 |
| - | 0.1 | 0.2 | - | 0.0917 |
| - | - | 0.3 | - | 0.0851 |
| - | - | 0.5 | - | 0.072 |
| - | - | 0.2 | 0.5 | 0.0992 |
| - | - | - | 1 | 0.1344 |
| - | - | - | 1.5 | 0.1693 |
| - | - | - | 2 | 0.2038 |
CONCLUSION
The mixed convection of nanofluid flow for the influence of Brownian and thermophoresis factors in association with the radiative heat flux is analysed in the existing discussion. The insertion of Darcy-Forchheimer inertial drag along with the volume fraction enhances the flow properties as well. The shooting-based numerical method, such as the traditional Runge-Kutta method, is used for the solution of the transformed model for various factors. Further, the significant outcomes for these parameters are described, and a few important characteristics are laid down here.
• Irrespective of the attendance/ non-attendance of the permeability of the medium the inertial drag by reason of the coefficient enhances inertial drag force, i.e., Darcy-Forchheimer the fluid velocity, and this causes the smooth retardation in the surface thickness.
• The mixed convective factor intended for the concurrence of the thermal buoyancy factor exceeds the fluid velocity, but a significant attenuation is observed for the regular and nanofluid buoyancy ratio parameters.
• Thermophoresis, along with the Brownian motion factor in occurrence Bi due to the heat flux boundary restrictions, favors in enhancing the fluid temperature throughout, but the flow along impermeable medium restricts it.
• The mutual consequence of thermophoresis as well as the Brownian factor, also shows a dual characteristic on the volume fraction profiles since the profile retards with increasing Brownian motion, but an opposite trend is observed for the thermophoresis.
• The retardation in the Brownian diffusion helps in enhancing the Lewis number, and this is the parameter that favors controlling the volume concentration for its increasing behaviour.
• The mixed convection parameter for the flow over a permeable medium augments the shear rate, but the regular, as well as nanofluid buoyancy ratio parameter, retards it significantly.
Finally, the present study has several practical applications, such as the findings of this study can be applied to improve the efficiency of energy systems that utilize nanofluids. By understanding the inertial drag and convective thermal surface effects, engineers can optimize the design of heat exchangers and thermal management systems for enhanced energy transfer. However, the behavior of nanofluids under convective thermal surfaces can be useful in the development of advanced cooling technologies. This knowledge can aid in designing efficient cooling systems for electronic devices, power plants, and other industrial processes. It has implications in biomedical engineering, particularly in the field of hyperthermia treatment. By understanding the inertial drag and the Soret effect, researchers can optimize the delivery of heat to target areas in tumor tissues, leading to improved therapeutic outcomes. However, one can extend their work by considering the nonlinear thermal radiation with the multiple slip effect, and those have several applications, as mentioned earlier. Also, instead of using the same methodology, authors can use the analytical methods likely, differential transform with Pede approximation, Variation parameter method, Homotopy perturbation method, etc. As a challenging area, the statistical approach along with Artificial Neural Network, can be employed for the optimized heat transfer rate.
NOMENCLATURE
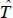 Temperature
Temperature
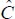 Solutal concentration
Solutal concentration
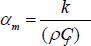 Thermal diffusivity
Thermal diffusivity
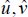 Components of velocity towards and axes
Components of velocity towards and axes
ρƒ∞ Density
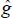 Gravitational Acceleration
Gravitational Acceleration
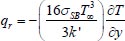 Thermal radiation
Thermal radiation
σSB Stefan-Boltzmann constant
k Thermal conductivity
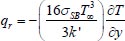 Kinematic viscosity coefficient
Kinematic viscosity coefficient
k' Mean absorption coefficient
ρ Density
βT Thermal expansion coefficient for volume
βc Solutal expansion coefficient for volume
kP* Permeability
ρP Density of the nano particles
DCT Soret type diffusivity
(ρC)P Effective heat capacity
DT Thermophoretic diffusion coefficient
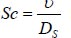 Schmidt number
Schmidt number
Ds Solutal diffusivity
µ Viscosity
DB Brownian diffusion coefficient
hƒ Convective heat transfer coefficient
ѱ Stream function
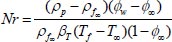 Nanofluid buoyancy ratio
Nanofluid buoyancy ratio
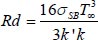 Prandtl number
Prandtl number
(ρC)ƒ The heat capacity of the fluid
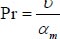 Lewis number
Lewis number
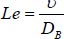 Consistent buoyancy ratio
Consistent buoyancy ratio
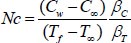 The local Grashof number
The local Grashof number
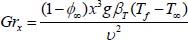 Brownian motion factor
Brownian motion factor
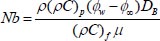 Soret number
Soret number
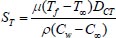 Biot number
Biot number
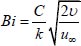 Thermophoresis parameter
Thermophoresis parameter
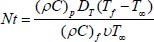 Darcy Number
Darcy Number
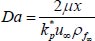 Drag Force
Drag Force
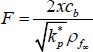 Mixed convection parameter
Mixed convection parameter
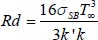 Radiation Parameter
Radiation Parameter
CONSENT FOR PUBLICATION
Not applicable.
AVAILABILITY OF DATA AND MATERIALS
Not applicable.
FUNDING
None.
CONFLICT OF INTEREST
Dr. S.R. Mishra is the Editorial Board Member of The Open Chemical Engineering Journal.
ACKNOWLEDGEMENTS
Declared none.


