New Analytical and Numerical Solutions of the Particle Breakup Process

1. INTRODUCTION

Population balance models of dispersed phases find many scientific and engineering applications including liquid-liquid, liquid-vapor and solid-liquid dispersions, nanoparticle physics, pharmaceutical industries, polymerization and bioreactors [1-11].

The complex structure of the PBE allows for an analytical solution only for some simple breakup kernels [8-10]. Several approximate resolution methods, such as weighted residuals [1-7], successive approximations [12], finite elements techniques [9, 13-16], finite volume scheme [17-22], fixed and moving pivot approaches [23], Monte Carlo methods [24-26] and method of moments with these several extensions such as QMOM, DQMOM, SQMOM and EQMOM [6, 27-29] have been widely studied.

For these moment methods, only a few moments are obtained. Therefore, after having computed these moments, it is necessary to reconstruct the distribution corresponding to the resulting droplet size distributions. Since the droplet size distributions generally constitute the key result to clearly evaluate the quality of the process, and the importance of the reconstruction procedure.

The key disadvantage of the MOM and its basic variants [5, 6, 30] is its incapacity to reconstruct the density function. Contrary to these numerical approaches, piecewise continuous solutions approach proposed in this work effectively and simultaneously provides the distribution and the different required moments without having to express the PBE in using moments.

Consequently, the different moments can be obtained by a simple integration of the solution. It should be noted that the present numerical method shows significant enhancement that avoids expressing population balance equation in terms of moments.

The aim of the present work is to show the advantage of this new proposed numerical method compared to the new analytical solutions of the (PBEs) using the Adomian decomposition method by considering the particle breakup process in batch and continuous flow. The term ‘particles’ might be referred to droplets, bubbles, crystals or grains, and may have several properties like size, composition, porosity, and enthalpy. The population balance equation model and the finite element method with the expansion coefficients approach for solving the breakup process will be described. Finally, the proposed numerical approach is compared with the analytical results for different assumed breakup kernels and physically relevant problems.

This paper is arranged as follows. In section two, we briefly introduce the population balance equation model. Then, in section 3, the finite element method with the expansion coefficients approach for solving the breakup process is described. Finally, the numerical approach is tested using analytical results obtained in this work.

1.1. Population Balance Equation for the Breakup Process in Continuous Flow:

The PBE that describes the evolution of the droplet number density, 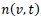in a continuous well-stirred vessel, with droplet formation and loss terms due to breakup, can be expressed as [1].

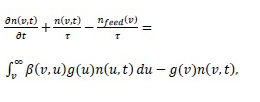(1)

where 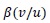is the diameter density distribution of daughter droplets and 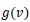is the droplet breakup frequency. The overall input flow determines the residence time τ of the dispersion. Thus, assuming a perfect mixer, where the outlet droplet volume distribution is always identical to the distribution inside of the vessel, 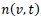, the resulting droplet entry and exit frequencies become 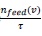and 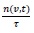, respectively. The two parts in the source term represent the droplet birth due to the generation of new droplets and the second term describes droplet death due to the breakup process.

In this work, the required breakup kernels to close Eq. (1) are shown in Table 1.

1.2. The Piecewise Continuous Solution Scheme

We consider the solution of the PBE for the droplet breakup in batch and continuous flow. As discussed in the introduction part, one of the most applied approaches for solving the PBE is the moment method. Alternatively, we present in this section, piecewise continuous solution scheme.

The principal idea of this method is to represent the distribution function as a Chebyshev truncated series as.

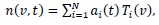(2)

where 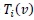, are the Chebyshev polynomials of the first kind of degree i which are orthogonal with respect to the weight function 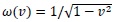on the interval [-1, 1] and satisfy the following recursive formula:

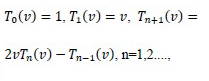(3)

and the unknown Chebyshev coefficients 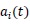remain to be computed.

Inserting 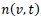into the PBE (1) and multiplying both sides of the breakup equation by a test function 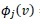and integrating from v=0 to ∞lead to

Table 1.

Case	Process	g(d)	β(d/u)	Feed Distribution	Initial Condition
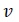
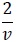
1	Batch			0
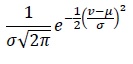
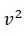
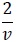
2	Batch			0
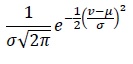
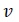
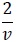
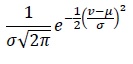
3	Continuous				0
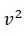
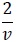
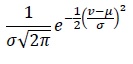
3	Continuous				0
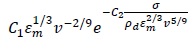
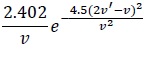
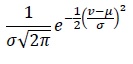
3	Continuous				0

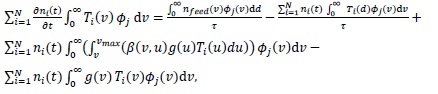(4)

Eq. (4) is then approached by:

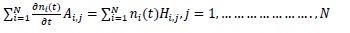(5)

with

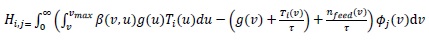(6)

and the mass matrix integral coefficients A_i,j can be written as.

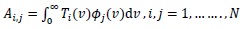(7)

It should be noted in the case of the pure Galerkin approximation 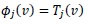and for the collocation approach 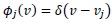, where the shifted Dirac delta functions are with V_j collocation points.

In the case in which the spatial domain is chosen as 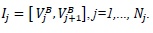. The points 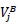and 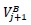are the boundary points for each interval. Let 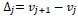be the width of an element and define the center of the interval I_j by V_j and the approximate solution is piecewise a polynomial of degree k then

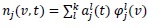, where 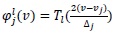and T_l is the lth Chebyshev orthogonal polynomial.

The initial values of 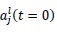are obtained up to order 3 as

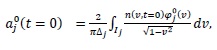(8)

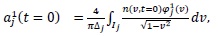(9)

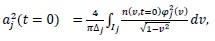(10)

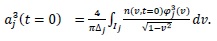(11)

For each interval I_j and each l = 0,..., k, the expansion coefficients 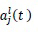are the degrees of freedom.

When the solution is obtained for the expansion coefficients, the k^th moment 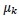of the number density function is then computed easily as

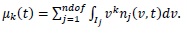(12)

2. THE DECOMPOSITION METHOD

To illustrate the basic concepts of the Adomian decomposition method, we consider the following nonlinear differential equation:

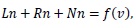(13)

where L is the linear operator chosen as the highest-order derivative, which must be easily invertible. The remainder of the linear operator is R and the nonlinear term is represented by Nn, and 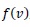is an inhomogeneous term.

Since L is invertible and using the initial condition, we have the canonical form:

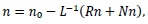(14)

by considering only the linear term, the Adomian decomposition method [31, 32] for the unknown function 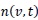can be written as

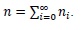(15)

The solution of the linear partial differential equation in the form (14) with the initial value

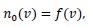(16)

can be obtained by the series (15) with the following recursion scheme

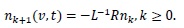(17)

2.1. Illustrative Tests Cases

The numerical solution using the finite element expansion coefficients of the breakup equation outlined above in batch and continuous systems will be compared to the following analytical solutions obtained by the decomposition method for the following cases 1, 2, 3 and 4:

Case 1: Breakup in a batch stirred vessel with a uniform daughter droplets distribution and linear breakup frequency with respect to the droplet volume.

Consider the breakup equation in the batch system given as:

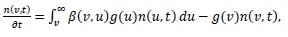(18)

by selecting the initial solution

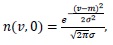
the ADM uses the following recursion relation to generate components of the solution as:

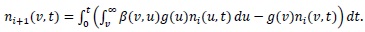(19)

Consequently, we can write

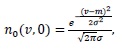(20)

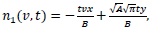(21)

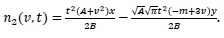(22)

Then, we find the solution by the general term as:

(23)

with the following closed solution

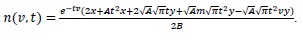(24)

Case 2: Breakup in a batch stirred vessel with a uniform daughter droplets distribution and parabolic breakup frequency with respect to the droplet volume.

By using the same algorithm which was used in Case 1 we get

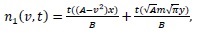(25)

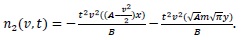(26)

The solution for this case is:

(27)

Case 3: Breakup in a continuous flow with a uniform daughter droplets distribution and linear breakup frequency with respect to the droplet volume.

Starting with

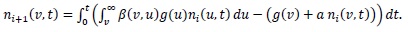(28)

Then we have with

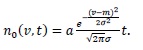(29)

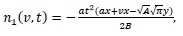(30)

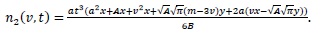(31)

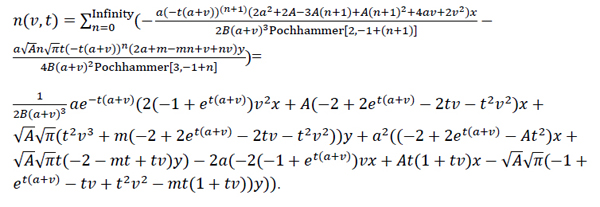(32)

Case 4: Breakup in a continuous flow with a uniform daughter droplets distribution and parabolic breakup frequency with respect to the droplet volume.

With the same algorithm in Case1 we obtain

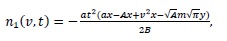(33)

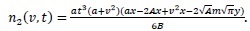(34)

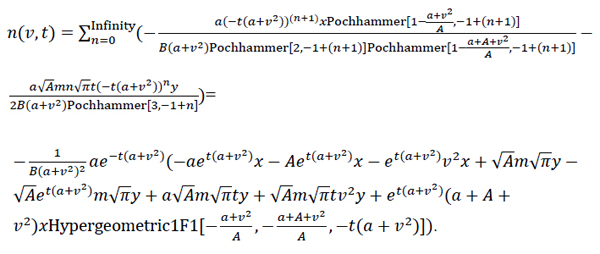(35)

With 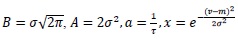and 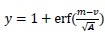, where m, σ and τ are the mean, standard deviation and the residence time for all cases, respectively.

Case 5: Breakup in a continuous flow with a physically relevant problem.

The inlet feed distribution, initial condition, daughter droplets distribution and breakup frequency are given in Table 1.

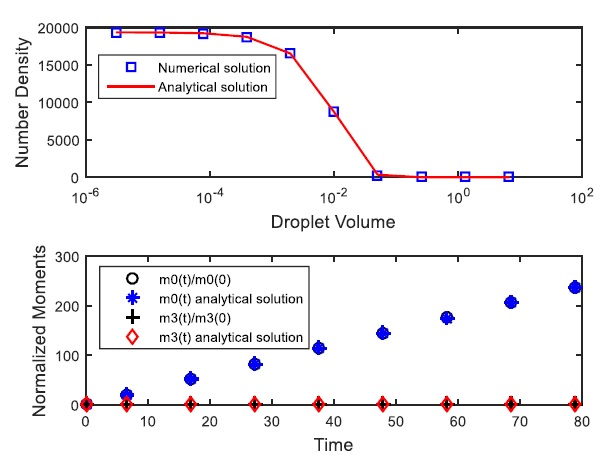
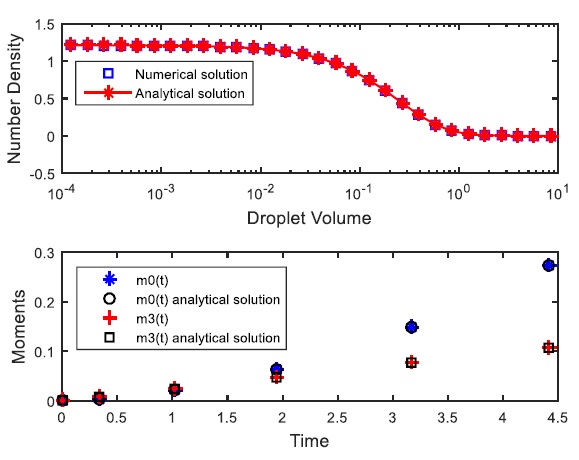
In Fig. (1), the complete droplets size distribution and the corresponding zeroth and third order moments, that are the total number and the total mass of droplets, respectively, are shown for the uniform daughter droplets distribution and linear breakup frequency in batch process with an initial condition supposed normal (Gaussian) distribution with mean m=3 and standard deviation σ=0.3. It is clearly shown from this figure that the zeroth moment increases, since more and more droplets are produced and the third moment is constant as expected by mass conservation. The prediction of the droplets size distribution as well as its related moments is very good accurate by both the finite element method with expansion coefficients based on the Chebyshev polynomials and the obtained analytical solution by the decomposition method.

Fig. (2) presents the complete droplet size distribution and the corresponding zeroth and third-order moments for the uniform daughter droplets distribution and parabolic breakup frequency in a batch process with an a Gaussian distribution initial condition with of the same mean and a standard deviation as in Case 1. The prediction of the droplet size distribution as well as its related moments is very good accurate by both the finite element method with expansion coefficients based on the Chebyshev polynomials and the analytical solution.

3. RESULTS

The numerical results presented in this article show that the present numerical method conserves the zeroth and third moments well enough.

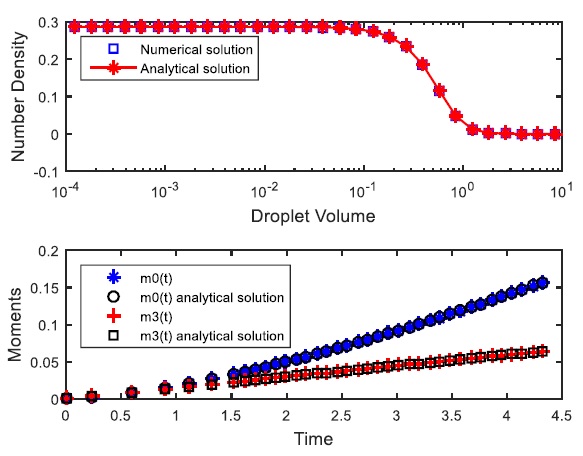
In Fig. (3), both analytical and numerical determined droplet size distribution and its corresponding moments for the initial distribution condition equal zero and the feed distribution are assumed a normal Gauss distribution with m = 3 and σ = 0.3 in a continuous flow with a uniform daughter droplets distribution and linear breakup frequency have been plotted. This figure includes the both the solutions for the variation of the zeroth and third-order moments. Once more, the agreement is excellent by the finite element method with expansion coefficients based on Chebyshev polynomials and the analytical solution.

Fig. (4) Once again, with m=3 and σ=0.3 for the Gauss feed distribution, the results for the droplet size distribution by the finite element method with the expansion coefficients based on the Chebyshev polynomials and the analytical solution for the Case 4 are accurate.

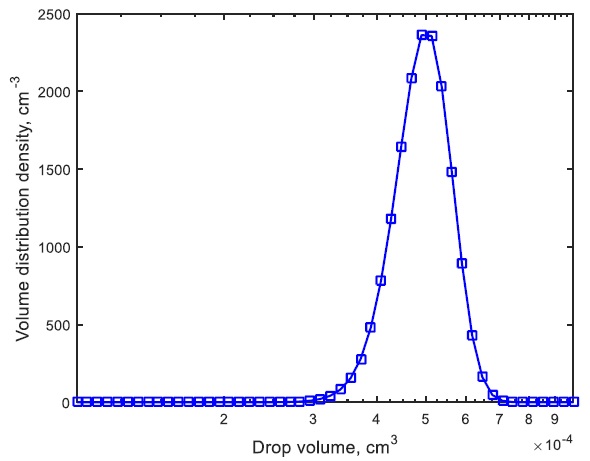
Fig. (5) presents numerical results corresponding to the physically relevant example as indicated in Table 1, with mean droplet volume μ = 0.5 10^-9m³ and σ = 0.625 10^-10m³ for the water-toluene system, and the agitation energy input ε_m = 0.15W/kg. In case 5, the analytical results are not available. We have therefore plotted only numerical results computed by the finite element method. The excellent agreement found between the present results and the previous predictions of [33] clearly illustrates the physical and numerical consistency of the present numerical method.

Fig. (6) shows the comparison of the relative merits of different discretization orders. We first present the solutions obtained with the number of degrees of freedom N_dof=96. There are 96 bins for the polynomial of order zero, 48 bins for the polynomial of order 1, 32 bins for the polynomial of order 3, and 24 bins for the polynomial of order 3.

Therefore, the consistency of the numerical results can be improved by expanding the order of the polynomial.

The accuracy of the numerical solutions at the final time using these four polynomials of order zero, 1, 2, and 3 is obtained against the analytical solution by the root-mean-square error norm whose errors are 0.2478, 0.2240, 0.0318 and 0.0011, respectively.

CONCLUSION

The droplet breakup in batch and continuous flow is described by the population balance equation (PBE), which represents the particle size distributions in a particulate process. The PBE is solved analytically and numerically. The proposed numerical method of the finite element method with expansion coefficients approach based on Chebyshev polynomials is employed to solve such equations with effectiveness and accuracy when compared to the exact solutions obtained by the Adomian decomposition method. The advantage of this present numerical method is that it does not require the reconstruction of the distribution from moments, unlike the original quadrature method of moments and its numerous extensions. With the proposed method, the construction of the distribution function and the moments is obtained straightforward.

The extension of the present numerical method to more complex systems, such as bubbly flows, requires further extension.

REFERENCES