Impact of Newtonian Heating on MHD Micropolar Fluid for the Influence of Heat Source
Abstract
Introduction:
The current analysis deals with the flow of time-independent conducting micropolar fluid past a stretching sheet. Furthermore, the influences of magnetic field strength and heat sources are also discussed in this study. The current study is important for the growing applications of magnetism in various chemical systems like pumping, transportation, trapping, sorting, separation, etc.
Aims:
In addition, the objective of the present exploration is the consideration of Newtonian heating conditions.
Methods:
Transformation of nonlinear PDEs of the flow phenomena into nonlinear coupled ODEs is done using suitable similarity variables, and these are handled by employing the “Runge-Kutta fourth-order” scheme in association with the “shooting technique”. The influence of flow characteristics proposed in this study is analyzed via graphs. The engineering coefficients for various parameters are simulated numerically and deployed through the table.
Results:
Finally, it was found that the rotational viscosity dominates over the fluid viscosity and enhances the momentum profile.
Conclusion:
An augmentation in the Prandtl number retards the fluid temperature and the application of applied magnetic field built up the resistance that retards fluid momentum.
1. INTRODUCTION
The recent era of science advances the emerging research areas based upon the application of polar fluids and dynamics relating to them. The specialty of this liquid is that several molecules are randomly oriented in the mixture of a fluid for which every part of the fluid molecule has its rotation and translation. Upon analysis, several interesting facts are developed that cannot be studied just by considering the earlier Newtonian fluids. For the appropriate suspensions, the models of micropolar fluids have an important role, and such fluids are biological fluids like blood flow, animal blood, etc., and lubricating oils. These particles experience a few micro rotations, such as rotational inertia, where various aspects of stress are vital for polar liquids. Depending upon the conservation laws for the constitutive equations, the impact of microrotation, as well as rotational inertia, is important. Therefore, both the momentum vectors, i.e., axial and angular momentum, are combined in the governing equation. For the prediction of micro-scale characteristics, the application of these micropolar fluids is vital and using a microrotation vector, the rotations can be further explained.
Due to the several applications in various areas on the flow of micropolar fluid over an expanding surface over the last decade, several researchers have devoted their contributions. Several examples can be considered for the applications, such as the manufacture of glass sheets, materials applied in metallurgy used for thermal and moisture treatment, and textile usages for processing polymers. For polymer processing, several research works have been conducted on the polar fluid by considering various aspects of chemical industries. Furthermore, the use of micropolar fluid has a crucial role in polymer extrusion, cable coating, and similar other processes in which heat transfer occurs through the stretching surface. As an experimental investigation, Crane [1] investigated the polar fluid over an expanding sheet. Based on his study, several authors have extended the study in several directions imposing different physical properties to eliminate the heat transport phenomenon. For every industrial process, the production process deals with the rate of heat transfer. Several studies [2-8] have been conducted on the flow of polar fluid. Free convection of polar fluid considering the Newtonian heating boundary condition over a vertical surface is studied by Chaudhary and Jain [9]. Makinde [10] examined the magnetohydrodynamic time-dependent flow for the various aspects of heat transfer properties using Newtonian heating under Navier slip conditions. An experimental investigation was conducted by Salleh et al. in a heat transfer on the boundary layer flow [11]. They have employed the Keller box numerical approach to solve the system of nonlinear governing equations. The stagnation point flow of polar fluid over a stretching surface is investigated by Nazar et al. [12]. Furthermore, Ishak et al. [13] extended their work on the time-independent MHD free and forced convection over a vertical stretching surface by considering a polar fluid. Mishra et al. [14] carried out their analysis on the free convection of micropolar fluid over a shrinking surface to examine the impact of the heat source. They conducted their work numerically to determine the significant contribution of the parameters involved in the flow problem. Ishak et al. [15] also proposed the MHD flow of polar fluids. They investigated the constant wall heat flux where the flow past a wedge. Srinivasacharya and RamReddy [16] worked on the free convection of the flow and heat transfer of micropolar fluid that was doubly stratified. Recently, Shamshuddin et al. [17] investigated the flow of chemically-reacting micropolar fluid past an inclined permeable surface for the behavior of radiative heat. They employed “Lie symmetry analysis” and numerical solutions for solving complex nonlinear problems characterized by the governing equations.
However, referring to the aforementioned literature, it can be concluded that heat transfer on MHD micropolar liquid in the presence of Newtonian heating over an expanding sheet due to the inclusion of a heat source is reported rarely. Earlier, studies on the thermal efficiency of polar liquid by imposing Newtonian heating past an expanding sheet have been carried out, but the use of applied magnetic field and additional heat source effects are not considered. Therefore, recent analysis confined to the time-independent MHD micropolar fluid is considered for the interaction of additional heat source, and Newtonian heating boundary condition is also imposed.
2. MATERIALS AND METHODS
2.1. Formulation and Solution
A time-independent flow of micropolar fluid over an expanding sheet is analyzed in the present literature. It is assumed that the sheet is along the
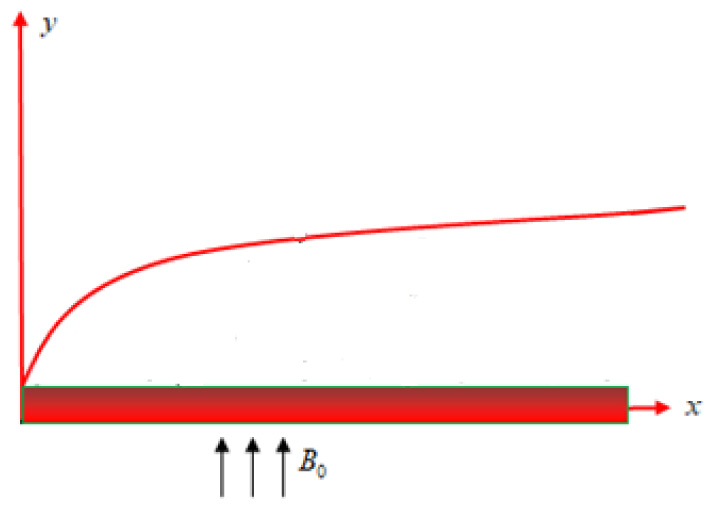
Following aforesaid assumptions, the constitutive flow equations associated with their boundary conditions are:
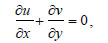 |
(1) |
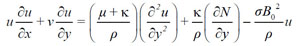 |
(2) |
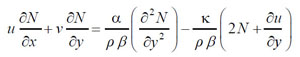 |
(3) |
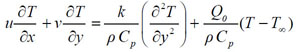 |
(4) |
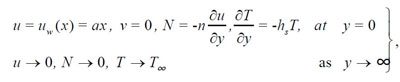 |
(5) |
where 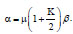 , the non-Newtonian characteristic eliminates, and the fluid is viscous. Here, n, the rotational parameter and
, the non-Newtonian characteristic eliminates, and the fluid is viscous. Here, n, the rotational parameter and
The similarity variable
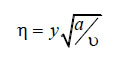 |
(6) |
The non-dimensional variables are defined as:
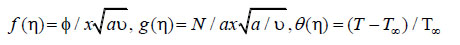 |
(7) |
The aforesaid transformations satisfy equation (1) automatically by considering
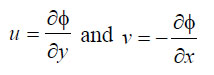 |
(8) |
Now, employing equations (6-8) and the stream function, the leading equations (2-4) are condensed to nonlinear coupled ODEs in conjunction with boundary conditions and are deployed as:
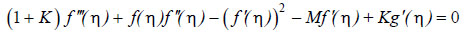 |
(9) |
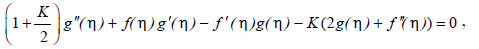 |
(10) |
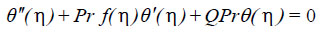 |
(11) |
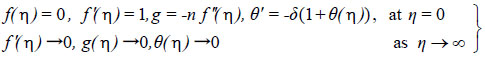 |
(12) |
where
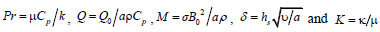 .
.
The local shear stress coefficient is
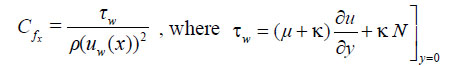 |
(13) |
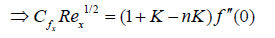 |
(14) |
The local couple stress
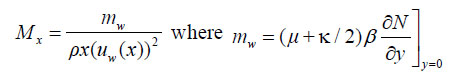 |
(15) |
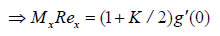 |
(16) |
Finally, the heat transfer rate
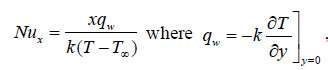 |
(17) |
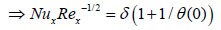 |
(18) |
3. RESULTS AND DISCUSSION
The present flow phenomena reveal the time-independent two-dimensional flow of conducting micropolar fluid to consider Newtonian heating conditions. Furthermore, the heat transport properties may be augmented with the inclusion of the heat source in the energy equation. The flow phenomena characterizing various profiles have been examined via graphs for the influence of a few of the imperative parameters involved in it. Also, the behaviors of the engineering coefficients are presented in the Table 1 illustrates the comparison of the current investigation with the work of Ramachandran et al. [18] in particular cases, and the result shows a good correlation.
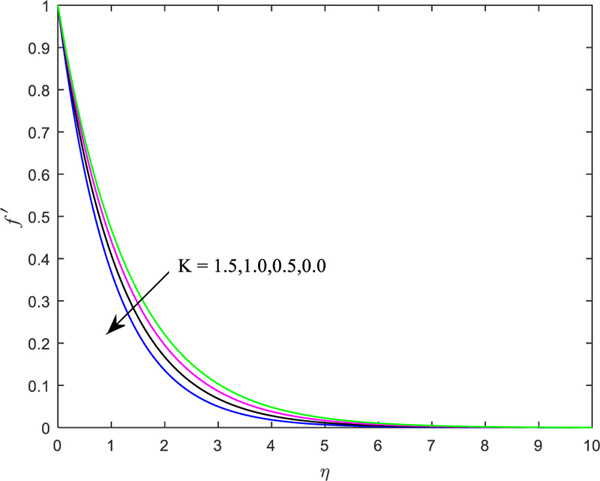
Figs. (2 and 3) portray the influence of material parameter (K) on the axial velocity distribution for the wall condition parameter,
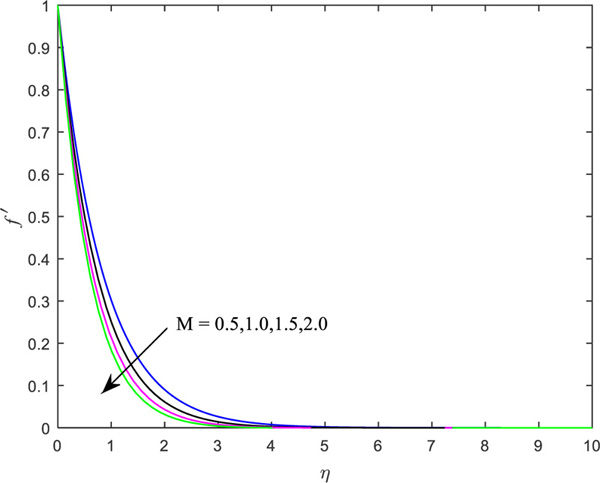
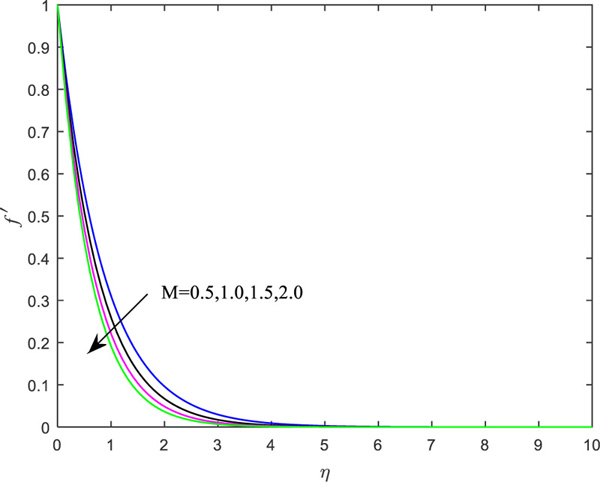
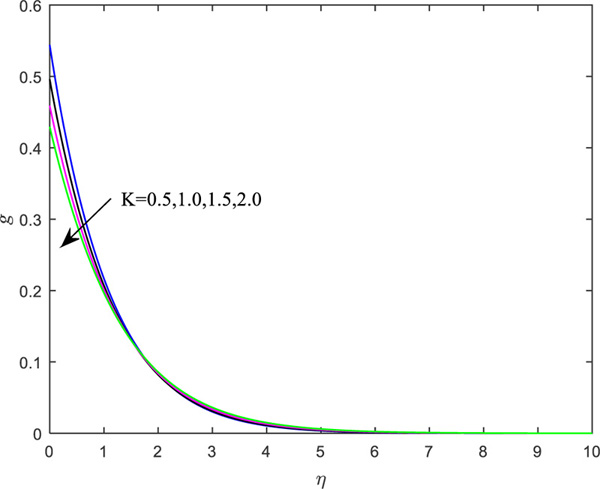
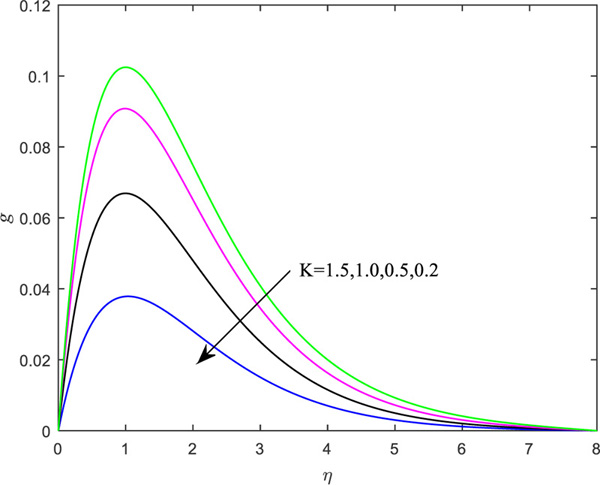
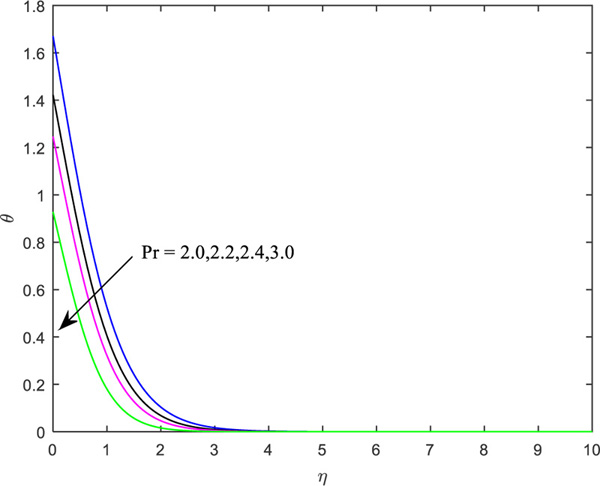
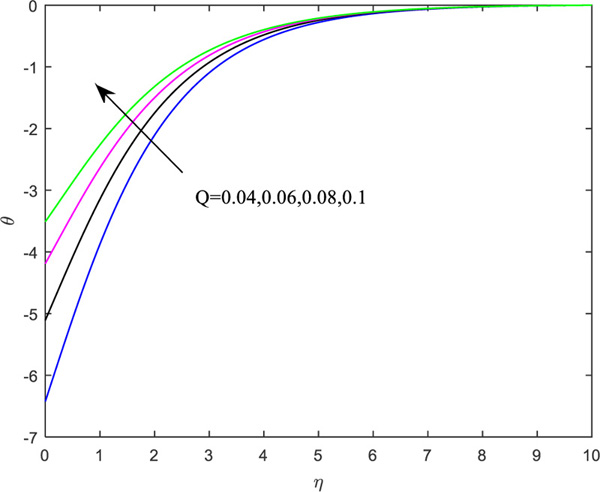
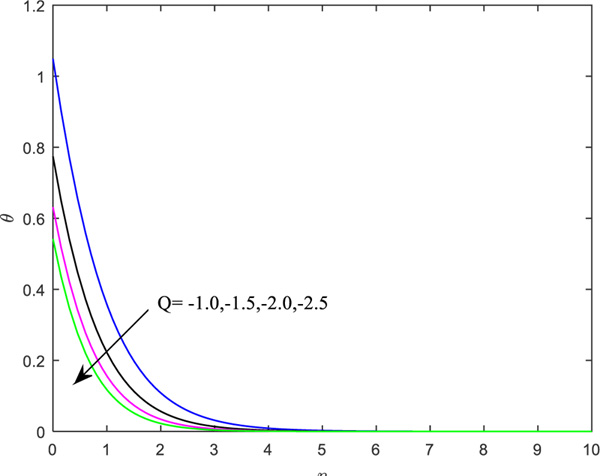
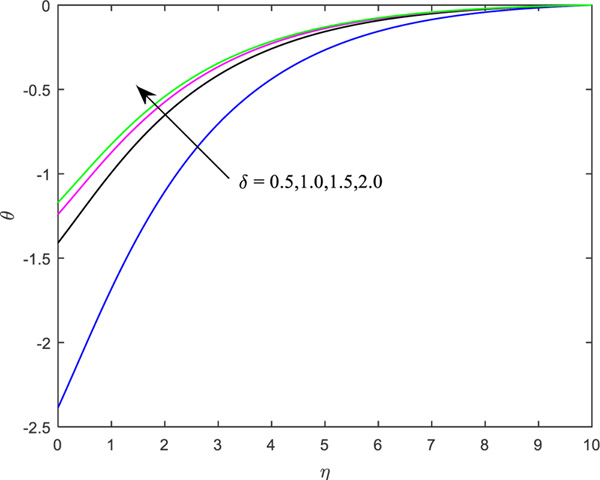
Table 2 portrays the weight of significant parameters on the engineering coefficients. It is marked that, with enhanced values of microrotation (n) and heat source (Q), the heat transfer rate retards but reverse impact is rendered for the material parameter, Newtonian heating parameter and Prandtl number, as the heat transfer rate enhances. Both the shear stress rate coefficients diminish for the augmentation in the material parameter. The shear rate boosts up, whereas the couple stress parameters decrease the increment in the boundary parameter. However, magnetic parameters favor the reduction in all the quantities of interest.
CONCLUSIVE REMARKS
The aforementioned results bring out the major aspects of the following conclusive remarks:
- Vortex viscosity dominates over the fluid viscosity, resulting in a significant increase in the fluid velocity.
- The appearance of the resistance offered by the Lorentz force reduces the fluid velocity.
- The thinning in the thickness of the bounding surface of the temperature is marked by an augment in the material parameter as well as the Newtonian heating parameter.
- The enhanced Prandtl number is favorable to increasing the thermal boundary layer thickness.
- The shear rate diminishes for the enhanced micropolar parameter.
CONSENT FOR PUBLICATIONS
Not applicable.
AVAILABILITY OF DATA AND MATERIAL
The data and supportive information are available within the article.
FUNDING
None.
CONFLICT OF INTEREST
Dr. S.R. Mishra is the associate editorial board member of the journal The Open Chemical Engineering Journal.
ACKNOWLEDGEMENTS
Declared none.